煤炭作为全球能源供给消费的主力，是全球能源消耗的重要组成部分之一。然而，矿井粉尘、冲击地压事故等严重制约井下开采的安全保障工作。煤层注水作为解决这一问题的重要手段，被广泛应用。在注水过程中，煤体同时受到应力与水压的作用，这种耦合作用使煤体产生形变，影响其渗透性能。因此，研究煤岩在水力耦合作用下的渗流与变形特征具有重要意义。

近年来，学者们对全应力应变条件下的砂岩、灰岩、花岗岩的渗透演化规律进行了大量的研究^[1-3]。WANG等^[4]、DAS^[5]对沉积岩全应力-应变过程中渗透规律进行了测定，发现在峰值强度之前，渗透率随轴向应力的增加而增加，在应变软化阶段，渗透率显著降低；FATT等^[6]通过对应力作用下砂岩渗透率的变化研究，提出了渗透率幂函数关系模型，并阐明了低压区渗透率变化更敏感的原因；WANG等^[7]进行了不同围压下的煤岩渗流试验，监测了煤岩的变形与渗透率演化情况，提出了考虑蠕变影响的渗透率改进模型；王军祥等^[8]通过试验推导了基于Kozeny-Carman公式的应变与渗透率的关系式；姜振泉等^[9]根据渗透试验所获得的渗透率-应变关系与应力应变关系，分析了岩石渗透性随变形变化的特点；杨永杰等^[10]研究了全应力-应变试验的试件渗透变化的率分析，研究表明应变-渗透率曲线与应力-应变曲线变化趋势基本一致，但表现出相对“滞后”的特点。

水力化措施常应用于煤体致裂增透过程，学者们在这一方面也进行了一系列研究并取得大量成果。CHERUBINI C^[11]基于Forchheimer方程分析了煤岩体的渗流规律；陈占清等^[12]研究了采动围岩的渗透特性，分析了采动围岩渗流系统的稳定性，构建了渗流系统的动力学方程；李顺才等^[13]研究了煤岩体水渗流与气体渗流系统的流固耦合分岔行为，建立了渗流动力学方程组，分析了破碎煤岩渗流的稳定性；BIOT^[14]建立了多孔介质水力耦合的三维数值模型，分析了多孔介质中孔隙压力与变形间的相互影响；SAVAGE^[15]运用三维固结理论研究了各向同性的弹性多孔介质中的渗流问题；刘海波等^[16]研究了水力冲孔与压裂耦合致裂增透技术对煤层煤体位移、应力分布、渗透率的影响，发现水力耦合致裂增透技术可以使煤体应力降低20%以上、渗透率提高35%以上。

值得注意的是，目前大多数研究主要集中于应力对渗透特性的影响^[17-19]。然而，实际注水工艺中的渗流过程受应力和水压的综合作用影响。目前关于水压对煤岩渗透特性和变形特征的影响机制缺乏深入探讨。因此，对煤岩试件开展全应力应变渗透特性试验，在探究应力对煤岩渗透率和体积应变特征影响规律的基础上，具体分析水压对于煤岩渗透性能和变形的影响机制。结合以上工作，进一步探究渗透率与体积应变相应关系模型。研究成果为煤层注水工作的实际应用以及提高煤层注水工作效率提供理论参考。

1.   全应力应变渗透特性试验

1.1   试验装置及加载路径

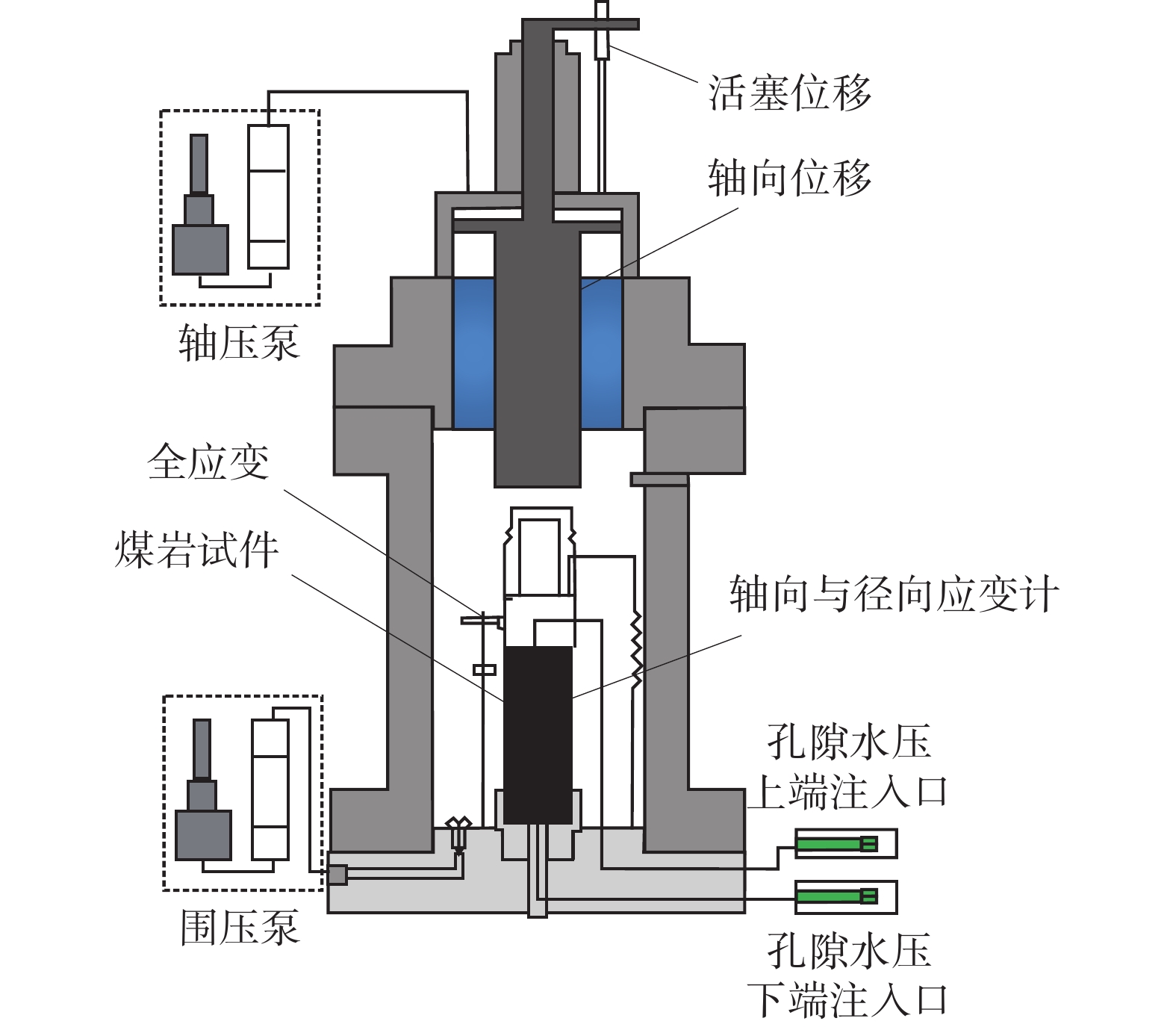
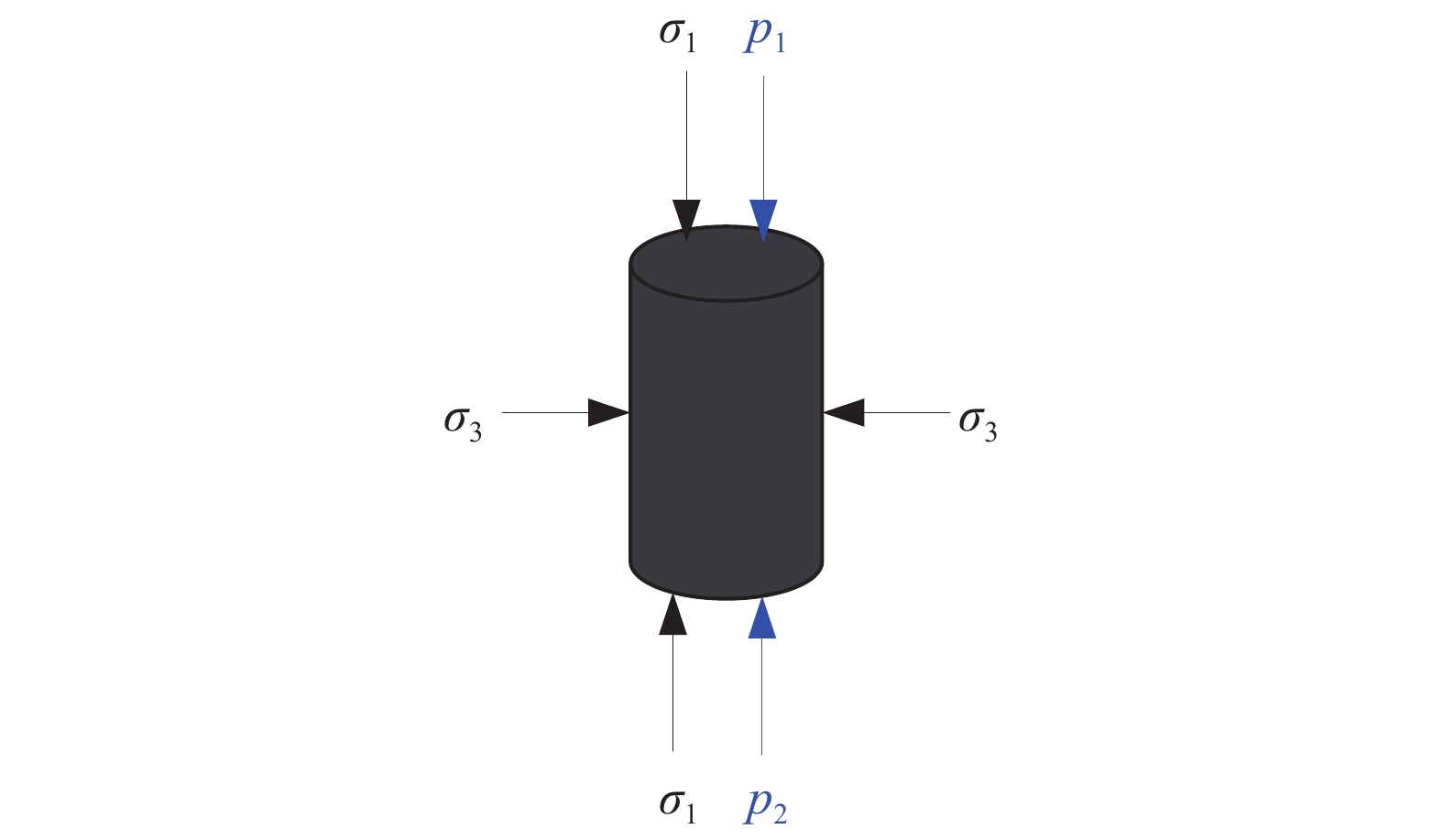
全应力应变渗透特性试验在MTS815.03电液伺服岩石试验系统上进行，试验压力加载方式示意图如图1所示，图中σ₁为轴压；σ₃为围压；p₁为上端水压；p₂为下端水压。试验装置注水渗透原理示意图如图2所示。

图  1  试验压力加载方式示意图

Figure  1.  Schematic diagram of test pressure loading mode

下载: 全尺寸图片 幻灯片

图  2  试验装置注水渗透原理示意图

Figure  2.  Schematic diagram of water injection and permeability principle of test device

下载: 全尺寸图片 幻灯片

1.2   试件制备及试验过程

试验所用试件取自三道沟煤矿，大块煤被加工成直径为50 mm，高度为100 mm的符合试验要求的圆柱形原煤标准试件。所制试件端面不平行度都在0.02 mm以内，加工后剔除表面有明显宏观裂隙的试件，按试验顺序依次编号。

在进行试验前测定各个试件的孔隙率，具体方法是先将加工好的试件烘干后称重，然后将试件浸泡于水中不少于7 d，使其达到饱和状态，取出再称重。根据干燥试件与饱水试件的质量，利用称重法测出各个试件的孔隙率。试验过程中，试验室内温度保持25 ℃。

试验釆用瞬态法测量煤岩渗透性，根据试验过程中计算机自动釆集的数据，计算岩石渗透率：

式中：$ {k} $为渗透率，m²；$ n $为数据采集行数；$ {\Delta }{p(i-1)} $为第$ {(i-1)} $行渗透压差，MPa；$ {\Delta }{p(i)} $为第$ {i} $行渗透压差，MPa。

1^#~6^#试件上端水压分别设置为3.5、3.5、7、3.5、7、10 MPa，下端水压分别设置为2、2、5.5、2、5.5、8.5 MPa，渗透压差均为1.5 MPa，围压分别设置为5、8、8、12、12、12 MPa。

7^#、8^#试件进行变水压试验，2个试件的围压条件均设置为12 MPa，变水压上限为10 MPa，下限为7 MPa。1^#~8^#试件的应力与孔隙水压作用试验试件参数见表1。

表  1  应力与孔隙水压作用试验试件参数

Table  1.  Parameters of coal samples for stress and pore water pressure test

试件 编号	高度/ mm	直径/ mm	围压/ MPa	渗透压 差/MPa	孔隙水 压/MPa	峰值应 力/MPa
1 #	100.01	49.90	5	1.5	3.5	40.77
2 #	99.82	49.83	8	1.5	3.5	62.94
3 #	99.88	49.58			7.0	48.65
4 #	99.92	49.67	12	1.5	3.5	71.69
5 #	100.04	49.75			7.0	60.22
6 #	99.86	49.94			10.0	60.57
7 #	99.72	49.82	12	1.5	10.0→7.0→10.0→7.0→3.5	未破坏
8 #	99.98	49.94	12	1.5	7.0→10.0→7.0→ 10.0→7.0→3.5	未破坏

下载: 导出CSV 

| 显示表格

2.   试验结果

2.1   应力对体积应变与渗透率的影响规律

根据全应力应变渗透特性试验所得数据，将渗透率、体积应变相结合，得到煤岩试件渗透率-体积应变（设定压缩量为正，扩张量为负）关系，试件渗透率-体积应变关系如图3所示。

图  3  试件渗透率-体积应变关系

Figure  3.  Relationship between permeability and volume

下载: 全尺寸图片 幻灯片

在应力加载初期，煤岩孔裂隙被压密，试件处于压缩变形阶段，渗透率随应力增大而降低。在围压12 MPa时，以5^#试件为例（图3（e）），加载一段时间后，煤岩渗透率较初始渗透率下降了75%；在加载后期，被压缩的煤岩变形进入扩展阶段，此时渗透率随应力增大平稳增加，煤岩体积应变开始升高，较之初始体积应变量增加15%；在应力加载达到煤岩峰值强度后，渗透率达到加载后期的峰值，相应的体积应变量也达到峰值。

围压对试件展现出一定的束缚效应，不同围压对于渗透率会产生不同的影响。围压5 MPa时，试件渗透率随应力增加呈现波动下降趋势；当围压为8、12 MPa时，渗透率呈现先减小后增大的变化规律。这是因为在较低的围压条件下（5 MPa），围压对试件裂隙扩展有一定束缚效果，但不占主导作用。轴压、水压与围压综合作用使渗透率表现为波动下降规律，由初始8.7118×10⁻⁷ m²下降到2.9865×10⁻⁷ m²；当围压参数设置较高时（8、12 MPa），在应力加载初期，试件产生压缩变形，其内部骨架颗粒逐渐被压密，孔隙连通性减弱，因此试验初期试样渗透率与应力大小呈负相关；在试验进行到一定阶段后，较高的轴压可以对试件产生更大的作用力，使试件内部的颗粒相互之间产生应力传递和相互作用。这种应力传递和相互作用使试件内部的裂隙扩张，煤岩变形进入塑性阶段。当水压较高时，水压会对试件内部的颗粒和裂隙产生额外的驱动力，通过孔隙介质的渗流，对试件作用产生力的传导作用。这一现象能够进一步强化轴压的作用，促使试件内部的裂隙扩张。因此，随着试验的进行，轴压及水压综合作用克服围压束缚效应，使试件内裂隙扩张，渗透率与应力大小呈正相关。

在围压同为8 MPa（图3（b）、图3（c））及12 MPa（图3（d）～图3（f））时，随轴压增大，渗透率先是不断减小，然后逐渐增大，相对应的体积应变先压缩后扩展。全应力应变试验过程中，当围压一定时，随着轴压的增长，在低轴压条件下，应力作用使试件内部孔裂隙闭合，试件体积变形处于压缩阶段，此时渗透率随应力增大而减小。当轴压持续加载，直至试件塑性破碎阶段后，孔裂隙逐渐扩张显现，试件体积开始增加，状态由压缩变形转变为扩张变形，此时渗透率从最低点回升。由此现象可以发现，轴压作用也是造成全应力应变渗透特性试验中煤岩试件渗透率先减后增规律的主要影响因素之一。

对试验数据分析可得，煤岩试件体积应变都经历了压缩、扩张2个阶段。对体积应变而言，试验过程中，轴向应变占据主导地位。渗透率对于体积变化特征存在着明显的响应关系，试件体积处于弹性压缩阶段时，试件内部裂隙闭合，渗透率下降；随着应力加载不断增加，试件逐渐进入塑性破碎阶段，试件内部裂隙扩展发育，渗透率逐渐上升。

2.2   水压对体积应变与渗透率的影响规律

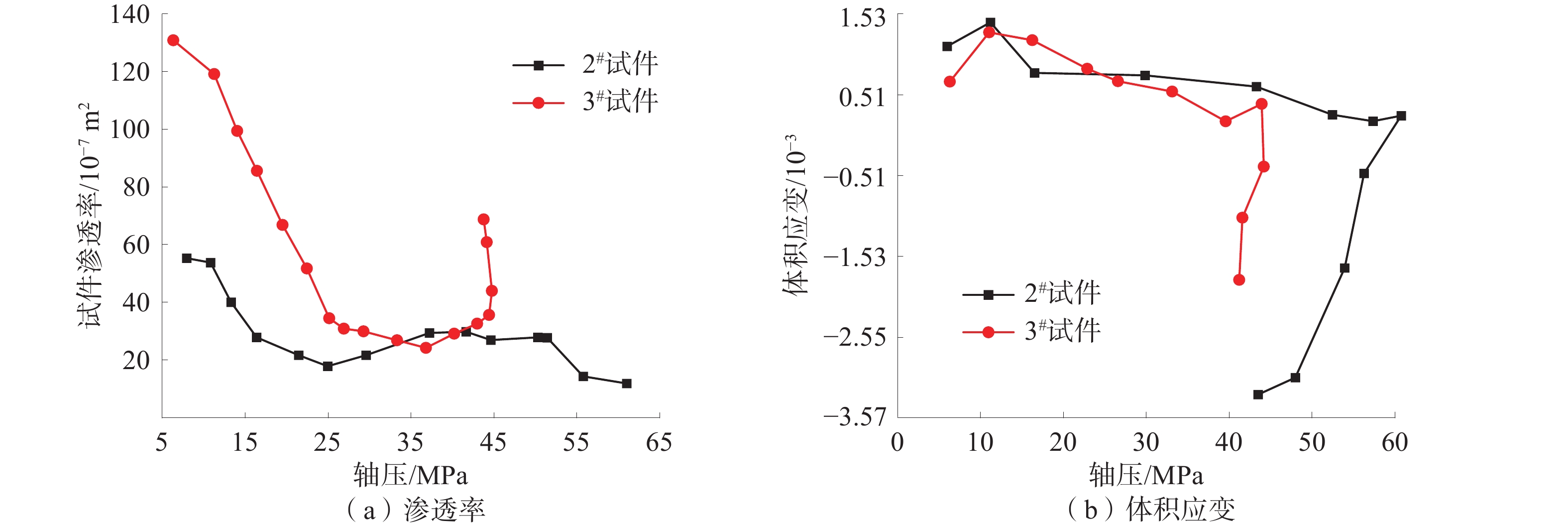
在应力条件相同时，孔隙水压影响煤岩渗流演化规律。2^#、3^#试件渗透率-体积应变关系如图4所示。

图  4  2^#、3^#试件渗透率-体积应变关系图

Figure  4.  Permeability-volume strain diagrams of 2^#, 3^# coal samples

下载: 全尺寸图片 幻灯片

相比2^#试件3.5 MPa的水压条件，3^#试件7 MPa的水压对煤岩试件体积应变和渗透率变化有较强的促进作用，其最大渗透率是2^#试件最大渗透率的4.5倍。较高的水压更有效地改善煤岩试件内部的孔隙连通性，促进孔裂隙发育的同时形成渗流通道，水更容易渗透进试件内部，进而使渗透率增加。而低水压条件下，孔隙连通性改善的效果较弱，导致渗透率增幅较小。两者的体积应变量在压缩阶段基本相同，但在进入扩张阶段后，在高压水力耦合作用下，3^#试件变形量远大于2^#试件。因此在应力条件相同时，较高的孔隙水压更能促进体积应变量的增加以及渗透率增长。

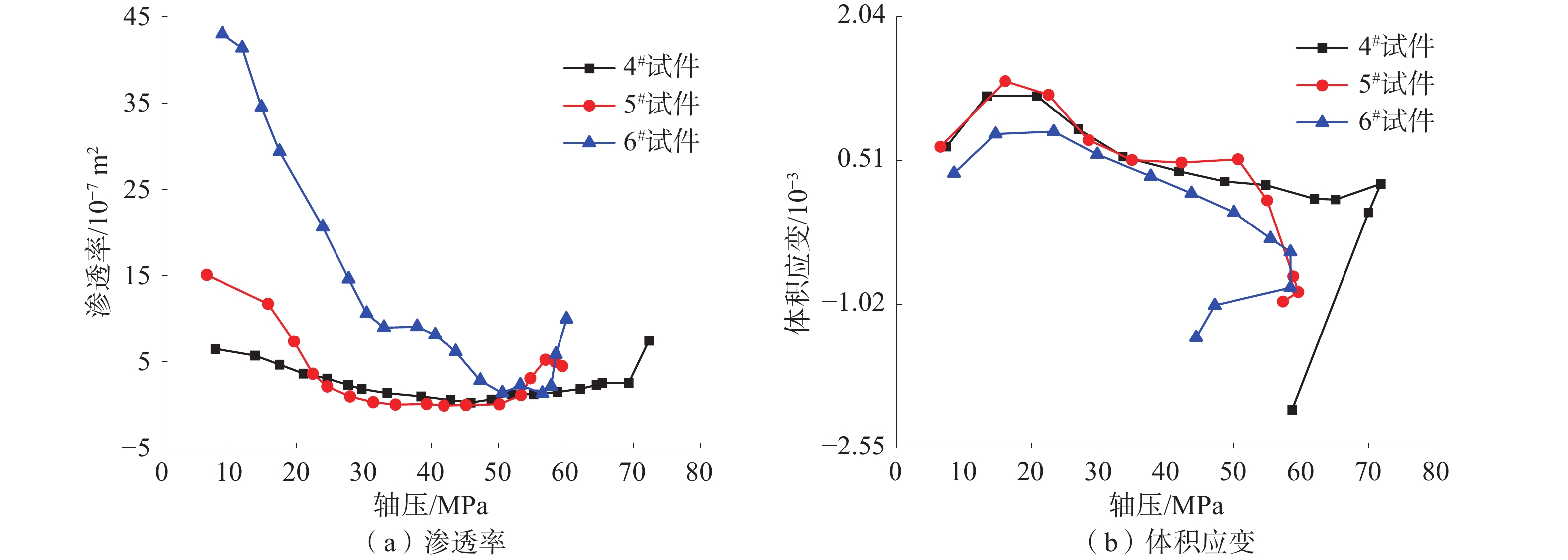
围压12 MPa，不同的水压条件，4^#、5^#、6^#试件渗透率-体积应变关系如图5所示。

图  5  4^#、5^#、6^#试件渗透率-体积应变关系图

Figure  5.  Permeability-volume strain diagrams of 4^#, 5^# and 6^# coal samples

下载: 全尺寸图片 幻灯片

由图5可以看出，孔隙水压越高，渗透率、体积应变波动幅度也越大；10 MPa水压条件下的6^#试件极值渗透率是4^#试件极值渗透率的3.36倍、是5^#试件极值渗透率的8.06倍；4^#、5^#试件渗透率变化比较平缓，4^#、5^#试件极值渗透率相较初始渗透率分别增加了27.5%、46.6%；在孔隙水压较高时，5^#、6^#试件的体积应变量变化更加明显，最小体积应变与最大体积应变相差12%，孔隙水压3.5 MPa时体积应变量波动不大。综上所述，在应力条件相同时，高水压促进了试件的裂隙扩展，裂隙扩展使煤样体积应变程度更加显著。因此，水压越高，对于体积应变和渗透率的影响作用就会越明显。

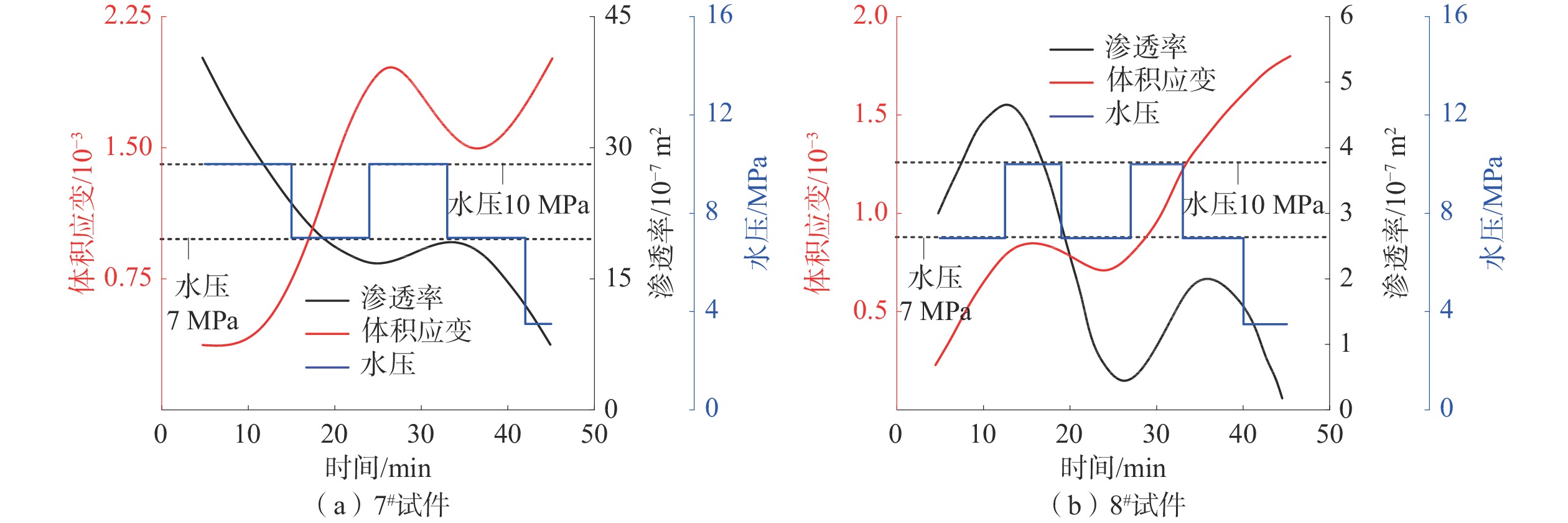
针对7^#、8^#试件在不同水压状态下的体积应变和渗透率变化进行分析，2个试件的变水压渗透率-体积应变关系如图6所示。

图  6  变水压渗透率-体积应变关系

Figure  6.  Relationship of variable hydraulic permeability-volume strain

下载: 全尺寸图片 幻灯片

针对煤岩试件的渗透率变化情况进行分析，以8^#试件为例，当水压从7 MPa升至10 MPa时，煤岩试件渗透率较刚开始试验阶段略有增加，增加程度为49.9%。当水压再次降至7 MPa时，其渗透率降至0.4996×10⁻⁷ m²，远远小于10 MPa时的渗透率，10 MPa水压时的渗透率是7 MPa时的8.65倍。当波动水压再次加载至10 MPa时，其渗透率仅恢复至1.8898×10⁻⁷ m²，亦小于之前该水压状态下的渗透率，但大于7 MPa时的0.4996×10⁻⁷ m²，在整个过程中，煤岩试件的渗透率总体上呈现波动下降趋势。与8^#试件类似，7^#试件的渗透率在整个变水压注水过程中也是呈现波动下降的趋势，末端渗透率相比于初始渗透率下降了82.5%。

综上所述，在同一试件的变水压试验过程中，由于水压的加载，煤岩受力情况发生变化。在初次加压阶段，煤岩的渗透率在水压作用下略有上升。但随着变水压注水的持续进行，试件受到的循环往复的水压作用，而水压首先会对煤岩孔隙结构产生压缩效果，使孔隙体积缩小。这一时期，煤岩变形处于压缩变形阶段，根据煤岩体积应变的变化趋势也说明试件处于压缩状态。因此，在变水压加载试验过程中，煤岩试件渗透率整体呈现波动下降趋势。但是，由于变水压注水是一个损伤积累的过程，试件在受到交变水压多次刺激后，孔裂隙结构会发生改变，煤岩变形将由压缩阶段转变为扩张阶段。在损伤积累达到临界点后，随水压加载，煤岩试件内部渗流通道开始增多，煤岩渗透率开始增加。然而，由于试验变水压循环次数较少，导致试件仍然停留在压缩变形阶段，渗透率未表现出增长态势。

2.3   渗透率与体积应变响应关系模型

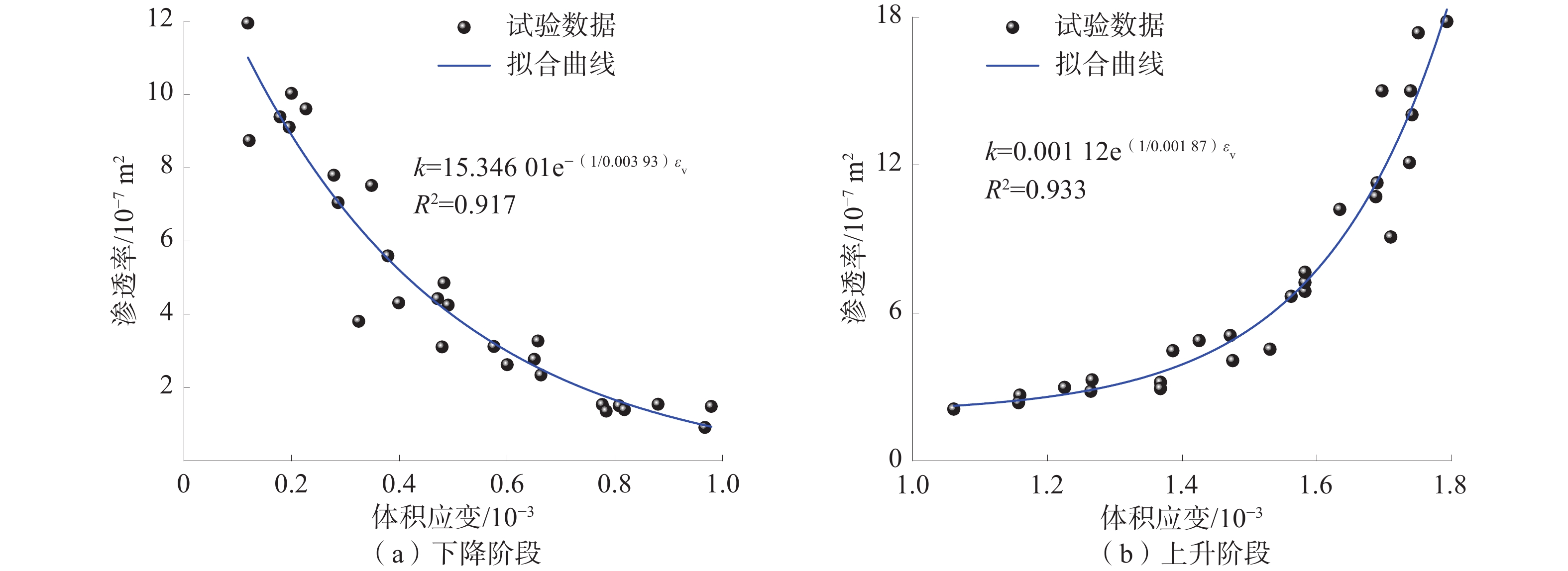
通过试验数据分析发现，渗透率与体积应变有着紧密的联系，渗透率的变化也存在明显的阶段性。根据1^#~6^#试件渗透率变化的阶段性规律，将整个试验过程分成2个阶段：渗透率随体积应变的降低阶段和渗透率随体积应变的上升阶段。整个试验过程按这2个阶段进行数据的分析处理，针对渗透率k对体积应变${{ \varepsilon }}_{{{\mathrm{v}}}} $响应数据进行拟合。得到相应的函数拟合公式：

式中：$ {{ \varepsilon }}_{\text{v}} $为体积应变；$ a $、$ b $、$ c $为常数。

式（2）是渗透率对于体积应变响应规律的拟合，体积应变和渗透率之间存在着指数函数关系。将试验开始的第1个渗透率作为初始渗透率，对渗透率-体积应变之间的响应关系进行拟合分析，得到以下拟合公式：

式中：$ {{k}}_{{0}} $为初始渗透率，m²。

将拟合出的函数公式与BRACE^[20]和王军祥等^[21]的研究成果进行比较分析，在不考虑初始孔隙率参数条件时，渗透率和体积应变之间是指数函数关系，且研究所得函数公式形式与其基本相同。煤岩渗透率-体积应变拟合关系如图7所示。

图  7  煤岩渗透率-体积应变拟合关系

Figure  7.  Fitting relationship between permeability and volumetric strain of coal

下载: 全尺寸图片 幻灯片

3.   结　语

1）在试验的初始阶段，煤岩处于裂隙压密状态，渗透率对于体积应变的响应是一致的，煤岩试件体积压缩，渗透率减小；当进入裂隙扩展阶段后，体积应变增大，渗透率也开始上升，在煤岩裂隙贯通后渗透率达到此阶段的极大值。

2）渗透率对于体积应变存在着明显的响应规律，通过对试验数据进行研究，发现两者之间存在指数函数关系，并与相关学者的研究成果进行对比分析，验证了研究得到的拟合函数的科学性和准确性。

3）在煤岩应力条件相同时，水压对煤岩试件变形与渗透性能演化产生影响。高水压促进了煤体的裂隙扩展，增加煤岩体积应变程度，孔隙水压越高，越能促进体积应变量的增加以及渗透率增长。

4）恒定水压条件下，煤岩渗透率呈现先减后增的趋势，高水压对于体积应变和渗透率的影响作用更明显。变水压条件下，次数较少的变水压无法使煤岩损伤达到由压缩变形到扩张变形的临界点，煤岩渗透率波动下降。但随变水压循环次数增加，煤岩变形进入扩张阶段，煤岩渗透率将会在水力耦合作用下开始增加。