Study on deformation law of roadway surrounding rock under dynamic disturbance
-
摘要:
煤矿深部开采时围岩处于高应力状态，动力扰动可能导致巷道围岩失稳，甚至发生冲击地压；因此，探究动力扰动条件下巷道围岩变形的影响因素，对围岩控制具有重要意义。基于弹性力学和应力波理论，分析了巷道围岩失稳机理；采用正交试验法和FLAC3D软件的动力学模块，探究了动力扰动条件下巷道围岩变形的影响因素。首先，根据极差、均值分析方法得到各因素对巷道围岩变形量的影响程度，由大到小依次为埋深、距离、扰动强度和扰动频率，埋深800 m、扰动强度20 MPa、距离9 m和频率5 Hz组合对巷道顶板及两帮变形量影响程度最大；埋深500 m、扰动强度5 MPa、距离18 m和频率20 Hz组合对巷道顶板及两帮变形量影响程度最小；其次，运用数值模拟方法分析了围岩位移、应力、塑性区和能量演化规律，验证了最大、最小组合的正确性；最终，通过多元线性回归数学模型对多因素作用下围岩顶板及两帮变形量进行预测，回归效果显著。
Abstract:The surrounding rock is in a state of high stress during deep mining of coal mine, and the dynamic disturbance may lead to the instability of the surrounding rock and even rock burst. Therefore, it is of great significance to study the influencing factors of the deformation of roadway surrounding rock under dynamic disturbance. Based on elastic mechanics and stress wave theory, the instability mechanism of roadway surrounding rock is analyzed. By using the orthogonal experimental method and the dynamics module of FLAC3D software, the influencing factors of roadway surrounding rock deformation under dynamic disturbance were investigated. Firstly, according to the method of range and mean value analysis, the influence degree of each factor on the deformation of roadway surrounding rock is obtained, from the largest to the smallest, it is buried depth, distance, disturbance intensity and disturbance frequency. The combination of buried depth of 800 m, disturbance intensity of 20 MPa, distance of 9 m and frequency of 5 Hz has the greatest influence on the deformation of the roof and two sides of the roadway. The combination of buried depth of 500 m, disturbance intensity of 5 MPa, distance of 18 m and frequency of 20 Hz has the least influence on the deformation of the roof and two sides of the roadway. Secondly, the displacement, stress, plastic zone and energy evolution of surrounding rock are analyzed by numerical simulation method, and the correctness of the maximum and minimum combination is verified. Finally, the multiple linear regression mathematical model is used to predict the deformation of surrounding rock roof and two sides under the action of multiple factors, and the regression effect is remarkable.
-
随着浅部资源逐渐枯竭，煤炭进入深部开采以后，开采环境变得更加复杂[1-6]；围岩不仅处于高应力状态，而且还会遇到爆破、断层滑移、机械振动等引起的动力扰动现象[7]；此时，动力扰动可能导致巷道失稳，甚至发生冲击地压[8]。因此，探究动力扰动巷道围岩变形的影响因素，对深部围岩控制具有重要意义。
国内外许多学者[9-10]运用室内试验和数值模拟等方法对动力条件下巷道变形进行了研究。刘冬桥等[11]通过自主研发的冲击岩爆试验装置，发现动静组合下诱发巷道冲击地压经历了裂纹产生、裂纹扩展、碎屑剥落和巷道大面积破坏4个阶段；TANG等[12]利用分离式霍普金森压杆实验装置，研究了冲击载荷下煤的动态力学响应和能量耗散行为；赵洪宝等[13]利用自制落锤式煤岩冲击加载实验装置，分析了冲击荷载对型煤内部微结构演化产生的影响机制；刘学生等[14]通过有限差分软件，研究了不同动载强度条件下深部超大断面硐室群围岩变形破坏规律；李夕兵等[15]运用颗粒流分析程序模拟了动载荷对高应力巷道稳定性的影响，分析了扰动波诱发高应力巷道失稳破裂的机制；王学滨等[16]通过连续−非连续方法耦合拉格朗日元和离散元，对周期冲击载荷下巷道顶板开裂机理进行了数值模拟研究；肖治民等[17]通过 FLAC3D 分析了深埋巷道底板水平应力和弹性应变能密度演化规律，得出巷道底板水平应力是底板冲击主要诱发因素。上述研究均考虑单一变量对围岩的影响，然而，动力扰动条件下巷道围岩变形受多种因素影响。
综上，运用弹性力学、应力波理论分析巷道失稳机理；考虑多种因素，运用正交试验和数值模拟手段探究动力扰动巷道围岩变形影响因素，为围岩控制提供指导。
1. 动力扰动条件下巷道围岩失稳原理
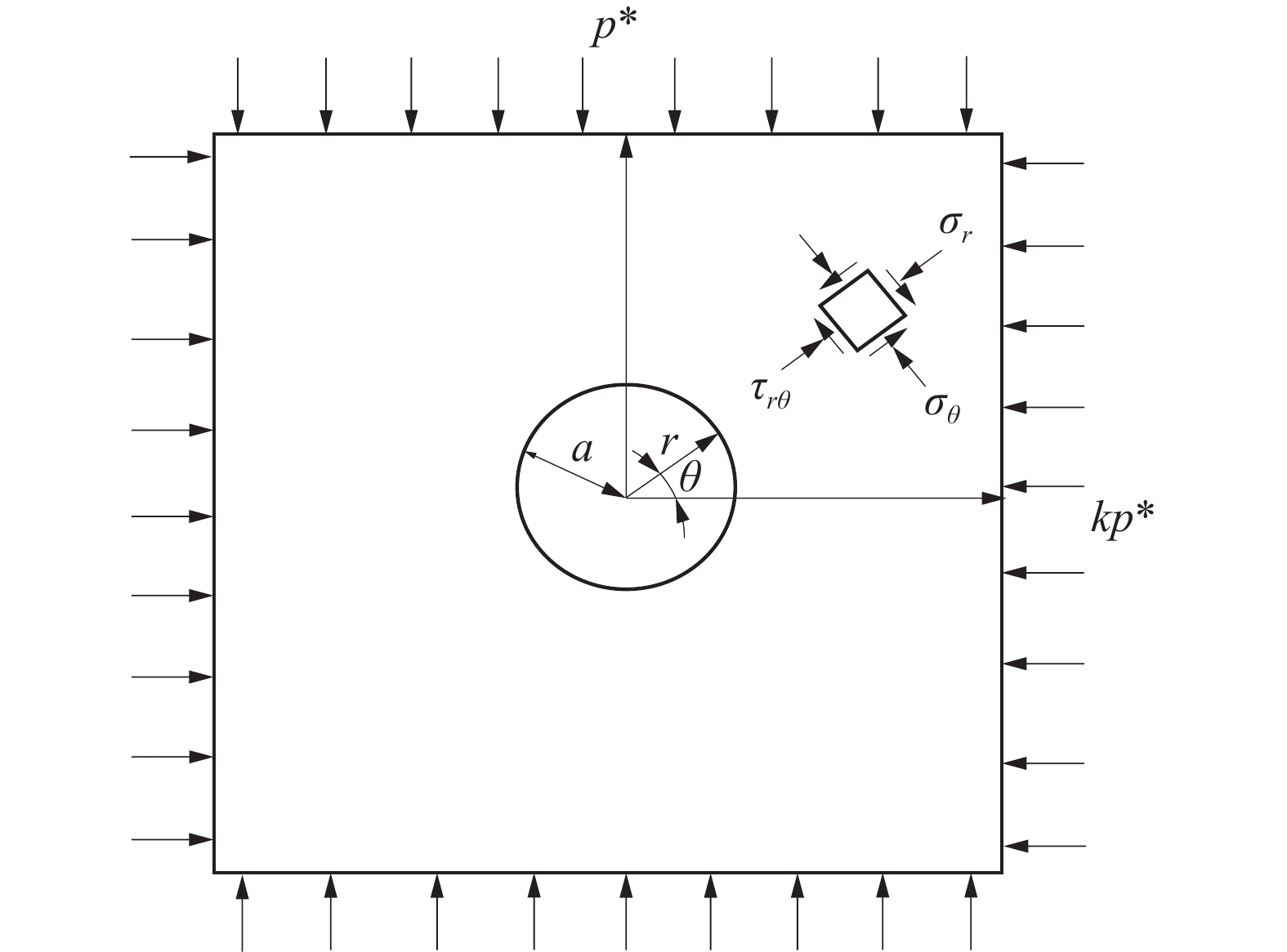
深部围岩开采时，围岩受到高静载应力作用。当遇到爆破、断层滑移、机械振动等引起的动力扰动可能导致巷道围岩失稳，甚至发生冲击地压。巷道围岩力学模型如图1所示。
根据弹性力学基尔希公式计算，得到距围岩中心$ r $处，与水平轴夹角θ的应力和位移如下[18]：
$$ \left\{ \begin{gathered} {\sigma _{{r}}} = \frac{{{p^ * }}}{2}\left[ {(1 + k)\left( {1 - \frac{{{a^2}}}{{{r^2}}}} \right) - (1 - k)\left( {1 - 4\frac{{{a^2}}}{{{r^2}}} + 3\frac{{{a^4}}}{{{r^4}}}} \right)\cos\; 2\theta } \right] \\ {\sigma _\theta} = \frac{{{p^ * }}}{2}\left[ {(1 + k)\left( {1 + \frac{{{a^2}}}{{{r^2}}}} \right) + (1 - k)\left( {1 + 3\frac{{{a^4}}}{{{r^4}}}} \right)\cos \;2\theta } \right] \\ {\tau _{{r\theta} }} = - \frac{{{p^ * }}}{2}\left[ {(1 - k)\left( {1 + 2\frac{{{a^2}}}{{{r^2}}} - 3\frac{{{a^4}}}{{{r^4}}}} \right)\sin\; 2\theta } \right] \\ \end{gathered} \right. $$ (1) $$ \left\{ \begin{gathered} {u_{{r}}} = \frac{{\left( {1{\text{ + }}v} \right){p^ * }{a^2}}}{{2Er}}\left\{ {(1 + k) - (1 - k)\left[ {4(1 - v) - \frac{{{a^2}}}{{{r^2}}}} \right]\cos\; 2\theta } \right\} \\ {u_\theta} = \frac{{\left( {1{\text{ + }}v} \right){p^ * }{a^2}}}{{2Er}}\left\{ {(1 - k)\left[ {2(1 - 2v) + \frac{{{a^2}}}{{{r^2}}}} \right]\sin\; 2\theta } \right\} \\ \end{gathered} \right. $$ (2) 式中：σr、σθ、σγθ分别为巷道围岩径向正应力、环向正应力、切向应力，MPa； ur、uθ分别为巷道围岩径向位移、环向位移，m；p*为上覆岩层的垂直应力，MPa；k为侧压系数；a为巷道围岩半径，m；r为受力点距巷道围岩中心长度，m；θ为受力点与水平轴的夹角，（°）； v为泊松比。
非圆形断面巷道的计算可以用“等效半径”为特征尺寸的等面积虚拟圆替代，等效半径公式为[19]：
$$ {r_0} = \omega \sqrt {\frac{S}{\pi }} $$ (3) 式中：r0为巷道等效半径，m；ω为巷道形状修正系数，根据文献[20]矩形断面巷道ω取1.2；S为巷道实际截面面积，m2。
假定距巷道中心rg处出现动力应力波扰动，该动力应力波自震源处穿岩层传播至巷道围岩表面时，扰动引起应力强度${\sigma _{\mathrm{t}}} $：
$$ {\sigma _{\mathrm{t}}} = {\sigma _0}{{\mathrm{e}}^{ - \lambda \left( {r_{\mathrm{g}} - {r_0}} \right)}} $$ (4) 式中：σ0为动力应力波的初始强度，MPa；λ为能量的衰减指数。
应力波传播至围岩表面时，将发生反射，根据围岩动量守恒、质量守恒及应力波边界条件，得到反射应力波引起的应力强度为：
$$ {\sigma _{{\mathrm{tf}}}} = {\sigma _{\mathrm{t}}}\left( {1 - \frac{{{\eta _{\text{w}}}}}{{{\eta _{\text{k}}}}}} \right)\left/\left( {1 + \frac{{{\eta _{\text{w}}}}}{{{\eta _{\text{k}}}}}} \right) \right.$$ (5) 式中：σtf为反射波应力强度，MPa；ηw为围岩表面波阻抗，g/（m2·s）；ηk为空气表面波阻抗，g/（m2·s）。
动力扰动下围岩失稳示意图如图2所示。巷道围岩表面波阻抗比空气表面波阻抗无穷大，入射波经过反射变成拉应力波，此时围岩受到拉应力，围岩处于拉伸状态；由于围岩具有抗压不抗拉的特点，当动力扰动强度较大时，围岩将会发生拉伸破坏；当拉伸破坏超过围岩极限抗拉强度时，围岩发生失稳破坏，综上所述，埋深、扰动强度、距离、介质阻抗等因素影响围岩变形。为此，在结合前人研究[21-24]基础上，考虑埋深、扰动强度、距离和频率对围岩变形的影响。
![]()
图 2 动力扰动下围岩失稳示意图Figure 2. Schematic diagram of surrounding rock instability under dynamic disturbance2. 动力扰动下巷道围岩变形数值模拟
2.1 静力学分析
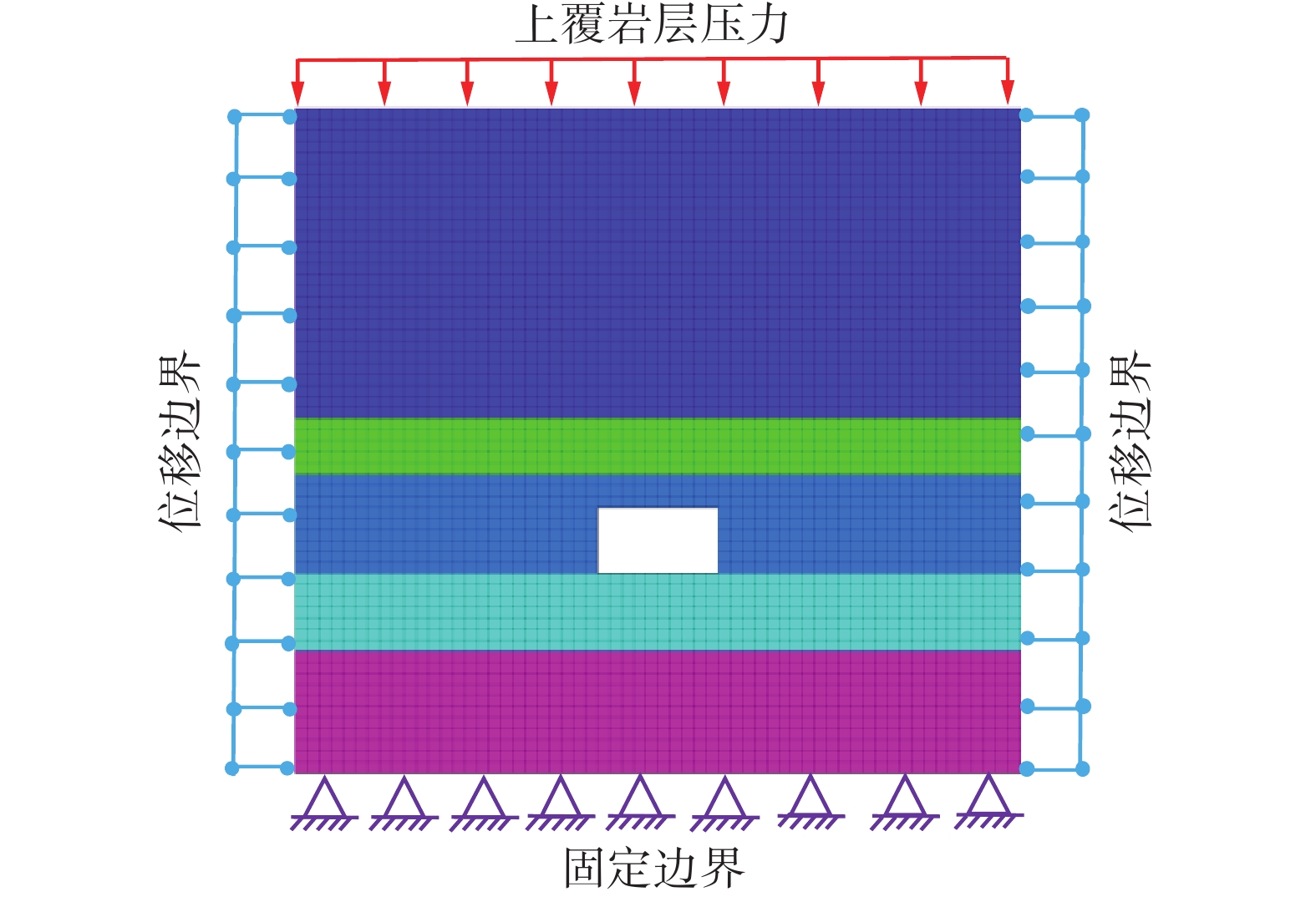
通过岩石切割机对试样加工为50 mm×50 mm×100 mm（长×宽×高）方柱体煤样和50 mm×25 mm（直径×高）圆柱体试样，通过单轴抗压、抗拉实验得到的煤样的基础力学参数见表1。依托漳村煤矿2606运输巷地质背景，采用FLAC3D软件构建30 m×20 m×30 m（长×宽×高）的三维模型，巷道顶板及两帮中间布置监测点，三维模型图如图3所示。对模型进行如下假设：不考虑岩性，煤岩体裂隙等因素的影响。模型为各向同性，符合摩尔库伦破坏准则。模型进行静力平衡，模型四周采用位移边界约束，底部采用固定边界约束，上部边界自由并承载上覆岩的均布载荷。静力学模型如图4所示。
表 1 基础力学参数Table 1. Basic mechanical parameters岩层 密度/
（g·cm−3）体积模
量/GPa剪切模
量/GPa黏聚力/
MPa内摩擦
角/（°）抗拉强
度/MPa砂岩 2.6 1.84 0.80 2.3 28 2.00 泥岩 2.5 1.79 0.97 1.9 30 1.60 煤 1.4 1.66 0.85 2.1 32 1.28 泥岩 2.5 1.79 0.97 1.9 30 1.60 砂岩 2.6 1.84 0.80 2.3 28 2.00 2.2 动力分析
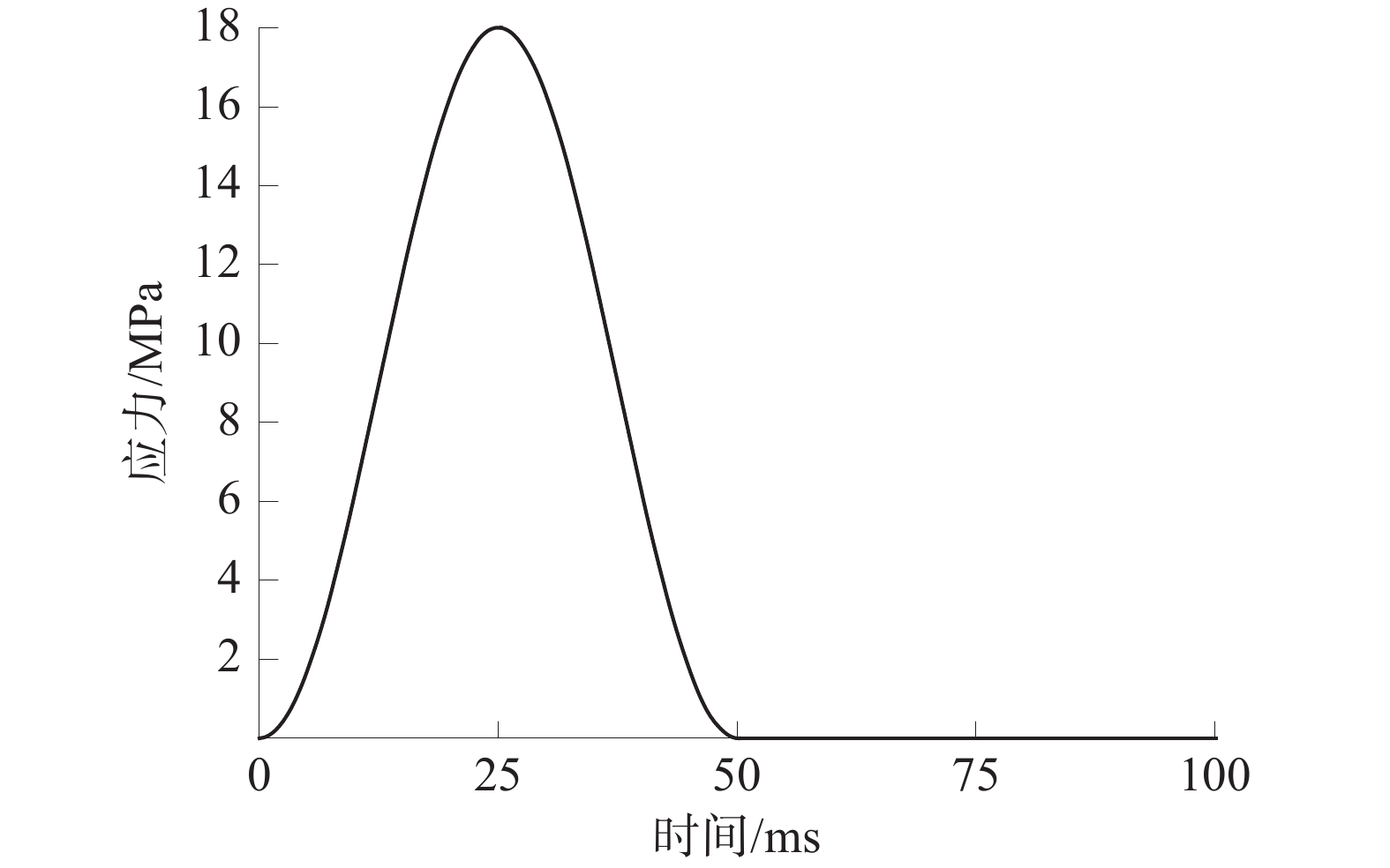
根据文献[25]将巷道受到的冲击波简化为半正弦波，利用Fish语言编写并且嵌入动力计算过程中。应力波时程曲线如图5所示。
采用的正应力波表达式如下，
$$ \sigma = \left\{ \begin{array}{ll} \sigma_{\mathrm{p}} (1 - \cos (2\pi ft))&(t \lt 1/f) \\ 0&(t \gt 1/f) \\ \end{array} \right. $$ (6) 式中：σ为应力，MPa；σp为峰值应力，MPa；f为扰动频率，Hz；t为动载加载时间，s。
模型在静力平衡之后，进行巷道开挖求解直至平衡，最后进行动力计算。根据文献[26]选取瑞丽阻尼，最小阻尼比为0.3%，中心频率 5.2 Hz。为减少应力波反射，模型四周均采用无反射边界，吸收法向入射波，模拟不同位置的动力扰动。动力学模型如图6所示。
2.3 正交试验设计
对于多因素试验的数理统计，正交设计试验法是1种适用的方法，即在全面试验中选出一些特征为均匀且整齐的代表点进行试验。在满足因素与水平均匀性的前提下，选择埋深H、动载扰动强度A、动载发生的位置与巷道顶板的垂直距离h、扰动频率f这4个主要因素，分别设置4个水平进行试验。因素和水平见表2，正交试验结果见表3。
表 2 因素和水平表Table 2. Factors and levels table因素 埋深/m 扰动强度/MPa 距离/m 频率/Hz 1 500 5 9 5 2 600 10 12 10 3 700 15 15 15 4 800 20 18 20 3. 正交试验分析
3.1 极差分析
极差分析是正交试验数据分析中的直观分析方法。极差分析可以得到各因素对巷道围岩变形的影响程度，根据影响程度可以确定最优和最差水平试验组合。针对上述正交试验得到的顶板垂直位移与两帮水平位移最大值，根据式（2）、式（3）求出各因素的极差。
$$ {K}_{ij}=\underset{d}{\overset{c=1}{{{\displaystyle \sum }}^{\text{}}}}{Y}_{ijc} $$ (7) 式中：Kij 为因素i在 j 水平的统计参数；Yijc （c = 1、2、3、···、d）为 c 组试验的试验结果。
$$ {k_i} = \max \{ {{{\overline K}_{i1}},{{\overline K}_{i2}},{{\overline K}_{i3}},{{\overline K}_{i4}}} \} - \min \{ {{{\overline K}_{i1}},{{\overline K}_{i2}},{{\overline K}_{i3}},{{\overline K}_{i4}}} \} $$ (8) 式中：Ki （i = A、B、C···）为i 因素的极差；$ {\overline K_{i{\text{j}}}} $为因素 i 第 j 水平的均值。
表 3 正交试验结果Table 3. Orthogonal experimental results编号 埋深/m 扰动强度/MPa 距离/m 频率/Hz 空值 顶板位移/mm 两帮位移/mm 1 1（500） 1（5） 1（9） 1（5） 1（0） −49.39 3.25 2 1（500） 2（10） 2（12） 2（10） 2（0） −40.73 2.45 3 1（500） 3（15） 3（15） 3（15） 3（0） −37.97 1.86 4 1（500） 4（20） 4（18） 4（20） 4（0） −36.56 1.18 5 2（600） 1（5） 2（12） 3（15） 4（0） −38.46 3.40 6 2（600） 2（10） 1（9） 4（20） 3（0） −49.22 3.55 7 2（600） 3（15） 4（18） 1（5） 2（0） −48.29 4.31 8 2（600） 4（20） 3（15） 2（10） 1（0） −46.25 3.93 9 3（700） 1（5） 3（15） 4（20） 2（0） −37.95 4.77 10 3（700） 2（10） 4（18） 3（15） 1（0） −47.11 5.97 11 3（700） 3（15） 1（9） 2（10） 4（0） −81.37 12.27 12 3（700） 4（20） 2（12） 1（5） 3（0） −75.93 13.49 13 4（800） 1（5） 4（18） 2（10） 3（0） −50.99 6.33 14 4（800） 2（10） 3（15） 1（5） 4（0） −67.71 10.18 15 4（800） 3（15） 2（12） 4（20） 1（0） −55.25 8.11 16 4（800） 4（20） 1（9） 3（15） 2（0） −91.01 13.28 根据极差分析可以得出，对顶板位移的影响强度从大到小为：埋深（KH=25.077）、距离（Kh=22.011）、扰动强度（KA=18.241）、频率（Kf=15.585），埋深对巷道顶板位移影响最大，频率对巷道顶板位移影响最小。同理得到各因素对两帮位移的影响程度从大到小为：埋深（KH=7.290）、距离（Kh=3.641）、扰动强度（KA=3.532）、频率（Kf=3.406），各因素对巷道围岩变形的影响见表4。
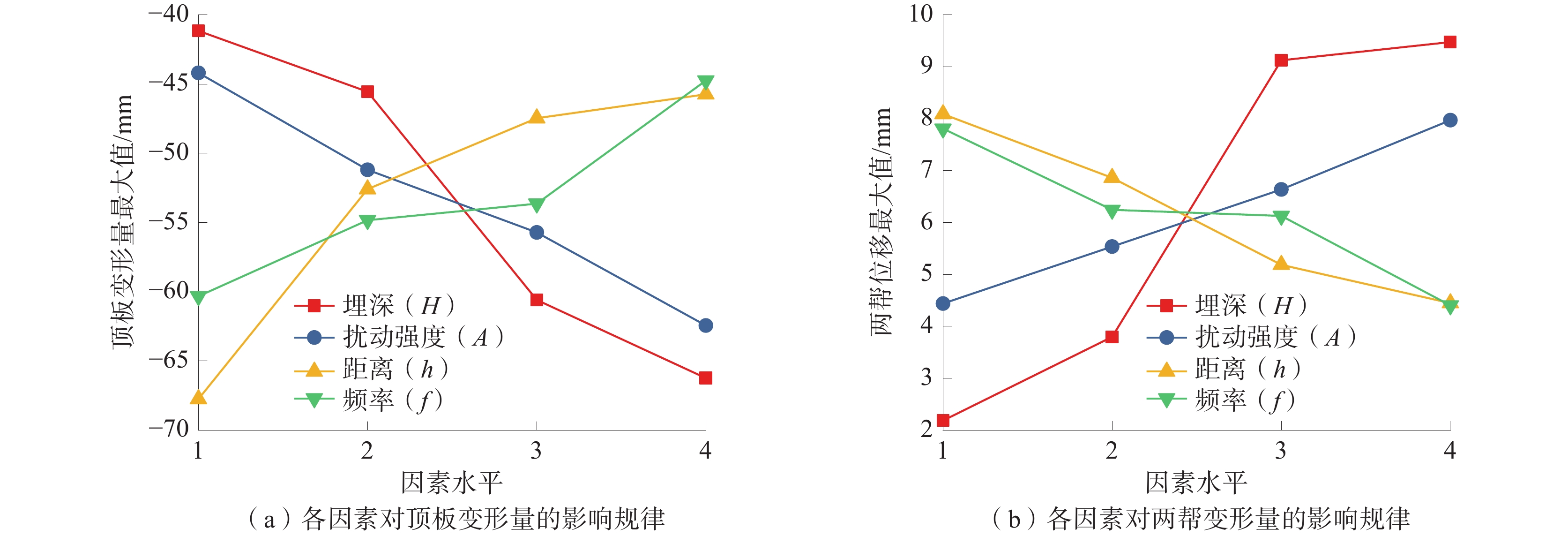
表 4 各因素对巷道围岩变形的影响Table 4. The influence of various factors on surrounding rock deformation水平 顶板位移的最大值/mm 两帮位移的最大值/mm 埋深因素 扰动强度因素 距离因素 频率因素 埋深因素 扰动强度因素 距离因素 频率因素 k1 −41.163 −44.197 −67.748 −60.330 2.185 4.438 8.088 7.808 k2 −45.555 −51.192 −52.593 −54.835 3.797 5.537 6.862 6.245 k3 −60.590 −55.720 −47.470 −53.638 9.125 6.637 5.185 6.127 k4 −66.240 −62.438 −45.737 −44.745 9.475 7.970 4.447 4.402 k 25.077 18.241 22.011 15.585 7.290 3.532 3.641 3.406 极差分析中各个均值（k1，k2，k3，k4）大小仅反映单因素在水平上的差异程度，需要通过因素指标综合比较得到各因素对巷道围岩变形量的影响规律，各因素对围岩变形量的影响如图7所示。
![]()
图 7 各因素对围岩变形量的影响Figure 7. The influence of various factors on surrounding rock deformation将巷道顶板和两帮位移量最大值作为指标时，由图7可以看出：当埋深800 m、扰动强度20 MPa、距离9 m、频率5 Hz时，对巷道顶板与两帮位移影响程度最大；当埋深500 m、扰动强度5 MPa、距离18 m、频率20 Hz时，对巷道顶板与两帮位移影响程度最小。综上可见，影响程度最大的组合为H4A4h1f1，影响程度最小的组合为H1A1h4f4。
3.2 巷道围岩位移场演化分析
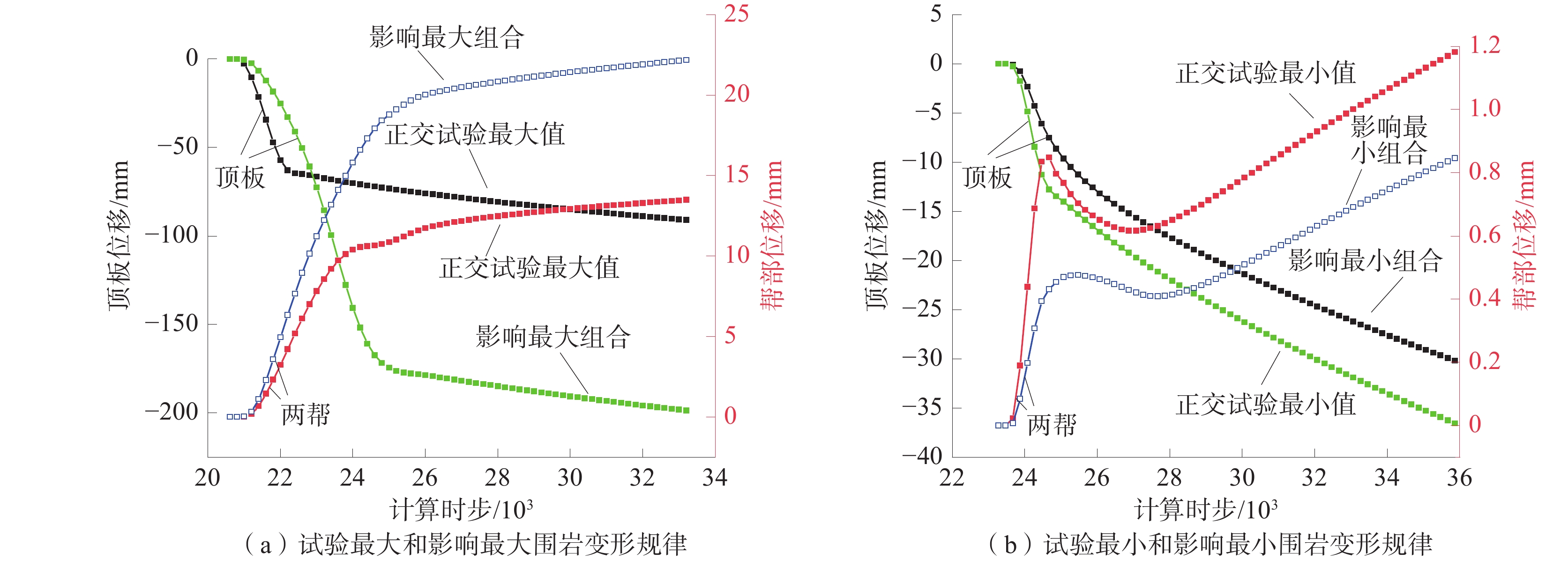
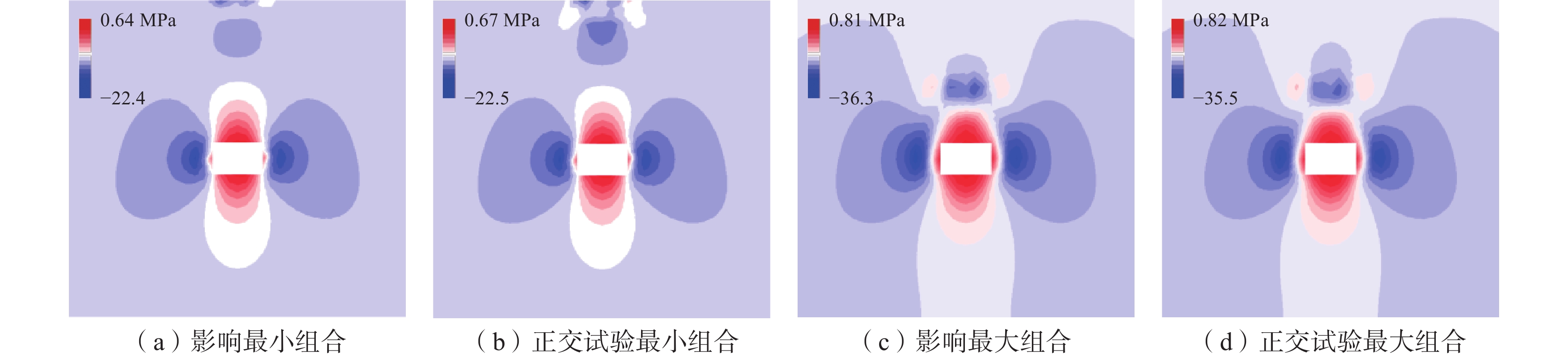
为验证影响程度分析结果，对上述巷道围岩变形量影响程度最大与最小组合进行数值模拟试验。不同组合下围岩变形规律如图8所示，巷道围岩的应力场演化规律如图9所示。
![]()
图 8 不同组合下围岩变形规律Figure 8. Deformation law of surrounding rock under different combinations![]()
图 9 不同组合下围岩应力分布Figure 9. Stress distribution of surrounding rock under different combinations由图8（a）可以看出影响程度最大组合试验结果，巷道顶板和两帮位移最大值分别为198.629 mm和22.18 mm，高于表3中16组试验的数据，说明该组合下围岩变形量最大是成立的；由图8（b）可以看出影响程度最小组合试验结果，巷道顶板位移最大值为30.19 mm，两帮位移最大值为0.845 mm，低于表3中16组试验的数据，说明该组合下对巷道围岩变形影响程度最小成立。
图9（a）为影响最小组合，此时两帮及顶板应力集中向深部转移，巷道两帮应力集中系数为1.86，应力集中在22.4 MPa；图9（b）为正交试验中最小值，巷道两帮应力集中系数为1.88，应力集中在22.5 MPa；图9（c）为影响最大组合，此时两帮及顶板应力集中向深部转移，巷道两帮应力集中系数为2.43，应力集中在36.3 MPa；图9（d）为正交试验中最大值，巷道两帮应力集中系数为2.33，应力集中在35.5 MPa。
综上所述，对巷道围岩变形影响最大与最小组合成立。
3.3 巷道围岩塑性区演化分析
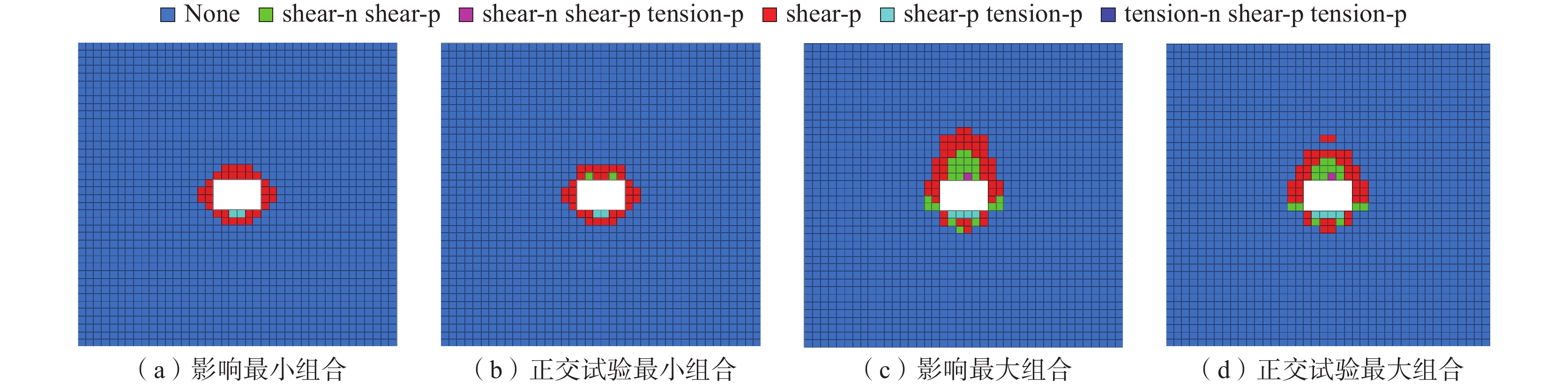
巷道围岩的塑性区演化规律进行分析不同组合下围岩塑性区分布如图10所示。
![]()
图 10 不同组合下围岩塑性区分布Figure 10. Distribution of plastic zone in surrounding rock under different combinations图10（a）比图10（b）的顶板塑性区破坏范围小，则影响程度最小组合选取成立；图10（c）为影响程度最大组合，顶板塑性破坏范围为7 m，底板有少量的拉伸破坏；图10（d）为正交试验中最大值，顶板塑性区破坏范围为4 m；图10（c）塑性区破坏范围大于图10（d）塑性区破坏范围。由此可见，巷道顶板受动力扰动影响最为严重，影响程度最大组合成立。
3.4 巷道围岩能量演化分析
动力扰动下巷道围岩失稳与围岩周围能量的积聚与释放有密切关联。利用FLAC3D中的Fish语言编写程序，提取上述4组试验中巷道围岩应变能密度，即微单元体在三向应力下的应变比能。
巷道围岩的能量演化规律如图11所示。
![]()
图 11 不同组合下围岩能量分布Figure 11. Energy distribution of surrounding rock under different combinations图11（a）为影响最小组合，巷道围岩周围应变能密度集中9.7 kJ/m3；图11（b）为正交试验最小值，围岩周围应变能密度集中在9.3 kJ/m3，由于动荷载扰动后，图11（a）比图11（b）巷道围岩破坏程度小，因此围岩周围集聚能量较大；图11（c）为影响最大组合，从图中可看出动荷载能量从上往下传播，呈椭圆形状包围在巷道周围，巷道围岩应变能密度集中在12.4 kJ/m3；图11（d）为正交试验最大值，巷道周围能密度集中在12.9 kJ/m3，由于动载扰动后，图11（c）比图11（d）巷道围岩破坏更严重，因此图11（c）中的巷道围岩集中能量较小。
3.5 方差分析
为验证上述极差分析结果正确性，根据下述公式分别对巷道围岩顶板、两帮位移进行方差分析。
$$ {S}_{\text{Q}}=\underset{n}{\overset{i=1}{{{\displaystyle \sum }}^{\text{}}}}\underset{d}{\overset{c=1}{{{\displaystyle \sum }}^{\text{}}}}{\left({Y}_{ij}\right)}^{2}-\frac{{T}^{2}}{{d}_{0}} $$ (9) $$ {S}_{j}=\frac{\underset{n}{\overset{i=1}{{{\displaystyle \sum }}^{\text{}}}}{\left({K}_{ij}\right)}^{2}}{{d}_{1}}-\frac{{T}^{2}}{{d}_{0}} $$ (10) $$ {S}_{{\mathrm{e}}}={S}_{\text{Q}}-\underset{m}{\overset{j=1}{{{\displaystyle \sum }}^{\text{}}}}{S}_{j} $$ (11) $$ X = \frac{{{S_j}/{q_j}}}{{{S_{\mathrm{e}}}/{q_{\mathrm{e}}}}} $$ (12) 式中：X为反应各因素是否具有显著性影响；SQ为全部试验数据变动平方和；Sj为变量因素变动平方和；Se为误差变动平方；n为试验因素的水平数；m为试验因素数量；d0为试验总次数；d1为各变量试验次数；T为试验指标累加量；qj为各因素自由度；qe为误差数据自由度。
对顶板位移进行方差分析，顶板位移方差分析结果见表5，对两帮位移进行方差分析，两帮位移方差分析结果见表6。依据X值分布表得到各因素的相伴概率P值。预先给定的显著水平为0.05，将P值与0.05进行比较，如果P值小于0.05，认为该因素对结果影响显著。
表 5 顶板位移方差分析结果Table 5. Results of variance analysis of roof displacement源 III 类平方和 自由度 均方 X 显著性（P值） 埋深（H） 1711.446 3 570.482 18.351 0.020 强度（A） 706.469 3 235.490 7.575 0.065 距离（h） 1201.524 3 400.508 12.883 0.032 频率（f） 500.195 3 166.732 5.363 0.101 表 6 两帮位移方差分析结果Table 6. Results of two sides of displacement variance analysis源 III 类平方和 自由度 均方 X 显著性（P值） 埋深（H） 164.647 3 54.882 37.633 0.007 强度（A） 27.431 3 9.144 6.270 0.083 距离（h） 32.365 3 10.788 7.398 0.067 频率（f） 23.242 3 7.747 5.312 0.102 根据表5可知：距离对顶板位移影响显著；根据P值，各因素对顶板位移影响程度由大到小为埋深（PH=0.020）、距离（Ph=0.032）、强度（PA=0.065）、频率（Pf=0.101），与极差分析结果一致。
根据表6可知：距离对顶板位移影响显著；根据P值，各因素对顶板位移影响程度由大到小为埋深（PH=0.007）、距离（Ph=0.067）、强度（PA=0.083）、频率（Pf=0.102），与极差分析结果一致。
3.6 多因素动力扰动条件下围岩变形回归模型
根据正交试验结果，构建多元线性回归数学模型。假设影响因素为x1、x2、x3、x4、···、xk，相应试验结果为y1、y2、y3、y4、···、yk, 则多元线性回归模型：
$$ y = {\beta _0} + {\beta _1}{x_1} + {\beta _2}{x_2} + \cdots + {\beta _k}{x_k} + \varepsilon $$ (13) 式中：y为围岩位移变形量，mm；$ {\beta _0} $为回归常数；$ {\beta _1} $、···、$ {\beta _k} $为回归模型系数；$ \varepsilon $为随机误差，mm。
根据表3中16组正交优化试验结果，通过SPSS软件对围岩顶板位移建立多元线性回归数学模型，顶板回归系数及显著性检验见表7，对围岩两帮位移建立多元线性回归数学模型见表8。
表 7 顶板回归系数及显著性检验Table 7. Roof regression coefficients and significance test of roof模型 非标准化
回归系数标准误差 标准化偏
回归系数回归系数
检验结果z显著性
水平Sigβ0 −45.784 6.984 −6.556 0.000 x1（埋深） −9.027 1.363 −0.622 −6.622 0.000 x2（振幅） −5.925 1.363 −0.408 −4.347 0.001 x3 （距离） 7.115 1.363 0.490 5.220 0.000 x4（频率） 4.795 1.363 0.330 3.518 0.005 表 8 两帮回归系数及显著性检验Table 8. Regression coefficients and significance test of the two sides模型 非标准化
回归系数标准误差 标准化偏
回归系数回归系数
检验结果z显著性
水平Sigβ0 2.154 1.680 1.282 0.226 x1（埋深） 2.720 0.328 0.766 8.293 0.000 x2（振幅） 1.170 0.328 0.330 3.567 0.004 x3 (距离） −1.260 0.328 −0.355 −3.841 0.003 x4（频率） −1.033 0.328 −0.291 −3.151 0.009 由表7可以看出：x1的非标准化为−9.027<0，回归系数检验z=−6.622，对应显著性水平 Sig=0.000<0.05，说明x1显著影响负向y，即x1越大y值越小，同理可证x2、x3、x4。经过检验回归系数具有统计学意义，顶板多元线性回归模型为：y=−45.784−9.027x1−5.925x2+7.155x3+4.795x4 。
由表8可以看出：x1的非标准化回归系数为 2.720>0，回归系数检验z=8.293，对应显著性水平 Sig=0.000<0.05，说明x1显著影响正向y，即x1越大y值越大，同理可证x2、x3、x4。经过检验回归系数具有统计学意义，两帮多元线性回归模型为：y=2.154+2.72x1+1.17x2−1.260x3+4.795x4 。
4. 结 语
1）根据正交试验结果，基于极值分析法，得到各因素对巷道顶板及两帮变形影响的敏感程度依次为埋深、距离、强度和频率，并根据方差分析方法验证，结果一致。在正交试验中，对巷道顶板和两帮变形影响最大的组合为H4A4h1f1；对巷道顶板和两帮变形影响最小的组合为H1A1h4f4。分析了围岩的位移、应力、塑性区和能量演化规律，证明了组合选取的正确性。
2）影响程度最大的组合时，顶板和两帮变形量分别为198.629 mm和22.18 mm，两帮应力集中系数为2.4，围岩应变能密度集中在12.4 kJ/m3；影响程度最小的组合时，顶板和两帮变形量分别为30.19 mm和0.845 mm，两帮应力集中系数为1.86，围岩应变能密度集中9.7 kJ/m3；前者顶板塑性区破坏范围是后者顶板塑性区破坏范围的3.5倍。
3）构建了各因素与巷道围岩顶板和两帮变形的多元线性回归方程。经Sig值检验，回归效果显著，为巷道围岩控制提供参考。
-
![]()
图 2 动力扰动下围岩失稳示意图
Figure 2. Schematic diagram of surrounding rock instability under dynamic disturbance
![]()
图 7 各因素对围岩变形量的影响
Figure 7. The influence of various factors on surrounding rock deformation
![]()
图 8 不同组合下围岩变形规律
Figure 8. Deformation law of surrounding rock under different combinations
![]()
图 9 不同组合下围岩应力分布
Figure 9. Stress distribution of surrounding rock under different combinations
![]()
图 10 不同组合下围岩塑性区分布
Figure 10. Distribution of plastic zone in surrounding rock under different combinations
![]()
图 11 不同组合下围岩能量分布
Figure 11. Energy distribution of surrounding rock under different combinations
表 1 基础力学参数
Table 1 Basic mechanical parameters
岩层 密度/
（g·cm−3）体积模
量/GPa剪切模
量/GPa黏聚力/
MPa内摩擦
角/（°）抗拉强
度/MPa砂岩 2.6 1.84 0.80 2.3 28 2.00 泥岩 2.5 1.79 0.97 1.9 30 1.60 煤 1.4 1.66 0.85 2.1 32 1.28 泥岩 2.5 1.79 0.97 1.9 30 1.60 砂岩 2.6 1.84 0.80 2.3 28 2.00 
下载: 导出CSV
表 2 因素和水平表
Table 2 Factors and levels table
因素 埋深/m 扰动强度/MPa 距离/m 频率/Hz 1 500 5 9 5 2 600 10 12 10 3 700 15 15 15 4 800 20 18 20
下载: 导出CSV
表 3 正交试验结果
Table 3 Orthogonal experimental results
编号 埋深/m 扰动强度/MPa 距离/m 频率/Hz 空值 顶板位移/mm 两帮位移/mm 1 1（500） 1（5） 1（9） 1（5） 1（0） −49.39 3.25 2 1（500） 2（10） 2（12） 2（10） 2（0） −40.73 2.45 3 1（500） 3（15） 3（15） 3（15） 3（0） −37.97 1.86 4 1（500） 4（20） 4（18） 4（20） 4（0） −36.56 1.18 5 2（600） 1（5） 2（12） 3（15） 4（0） −38.46 3.40 6 2（600） 2（10） 1（9） 4（20） 3（0） −49.22 3.55 7 2（600） 3（15） 4（18） 1（5） 2（0） −48.29 4.31 8 2（600） 4（20） 3（15） 2（10） 1（0） −46.25 3.93 9 3（700） 1（5） 3（15） 4（20） 2（0） −37.95 4.77 10 3（700） 2（10） 4（18） 3（15） 1（0） −47.11 5.97 11 3（700） 3（15） 1（9） 2（10） 4（0） −81.37 12.27 12 3（700） 4（20） 2（12） 1（5） 3（0） −75.93 13.49 13 4（800） 1（5） 4（18） 2（10） 3（0） −50.99 6.33 14 4（800） 2（10） 3（15） 1（5） 4（0） −67.71 10.18 15 4（800） 3（15） 2（12） 4（20） 1（0） −55.25 8.11 16 4（800） 4（20） 1（9） 3（15） 2（0） −91.01 13.28
下载: 导出CSV
表 4 各因素对巷道围岩变形的影响
Table 4 The influence of various factors on surrounding rock deformation
水平 顶板位移的最大值/mm 两帮位移的最大值/mm 埋深因素 扰动强度因素 距离因素 频率因素 埋深因素 扰动强度因素 距离因素 频率因素 k1 −41.163 −44.197 −67.748 −60.330 2.185 4.438 8.088 7.808 k2 −45.555 −51.192 −52.593 −54.835 3.797 5.537 6.862 6.245 k3 −60.590 −55.720 −47.470 −53.638 9.125 6.637 5.185 6.127 k4 −66.240 −62.438 −45.737 −44.745 9.475 7.970 4.447 4.402 k 25.077 18.241 22.011 15.585 7.290 3.532 3.641 3.406
下载: 导出CSV
表 5 顶板位移方差分析结果
Table 5 Results of variance analysis of roof displacement
源 III 类平方和 自由度 均方 X 显著性（P值） 埋深（H） 1711.446 3 570.482 18.351 0.020 强度（A） 706.469 3 235.490 7.575 0.065 距离（h） 1201.524 3 400.508 12.883 0.032 频率（f） 500.195 3 166.732 5.363 0.101
下载: 导出CSV
表 6 两帮位移方差分析结果
Table 6 Results of two sides of displacement variance analysis
源 III 类平方和 自由度 均方 X 显著性（P值） 埋深（H） 164.647 3 54.882 37.633 0.007 强度（A） 27.431 3 9.144 6.270 0.083 距离（h） 32.365 3 10.788 7.398 0.067 频率（f） 23.242 3 7.747 5.312 0.102
下载: 导出CSV
表 7 顶板回归系数及显著性检验
Table 7 Roof regression coefficients and significance test of roof
模型 非标准化
回归系数标准误差 标准化偏
回归系数回归系数
检验结果z显著性
水平Sigβ0 −45.784 6.984 −6.556 0.000 x1（埋深） −9.027 1.363 −0.622 −6.622 0.000 x2（振幅） −5.925 1.363 −0.408 −4.347 0.001 x3 （距离） 7.115 1.363 0.490 5.220 0.000 x4（频率） 4.795 1.363 0.330 3.518 0.005
下载: 导出CSV
表 8 两帮回归系数及显著性检验
Table 8 Regression coefficients and significance test of the two sides
模型 非标准化
回归系数标准误差 标准化偏
回归系数回归系数
检验结果z显著性
水平Sigβ0 2.154 1.680 1.282 0.226 x1（埋深） 2.720 0.328 0.766 8.293 0.000 x2（振幅） 1.170 0.328 0.330 3.567 0.004 x3 (距离） −1.260 0.328 −0.355 −3.841 0.003 x4（频率） −1.033 0.328 −0.291 −3.151 0.009
下载: 导出CSV
-
[1] 张俊文,宋治祥,刘金亮,等. 煤矿深部开采冲击地压灾害结构调控技术架构[J]. 煤炭科学技术,2022,50(2):27−36. ZHANG Junwen, SONG Zhixiang, LIU Jinliang, et al. Architecture of structural regulation technology for rock burst disaster in deep mining of coal mine[J]. Coal Science and Technology, 2022, 50(2): 27−36.
[2] 李胜,王箫鹤,范超军,等. 冲击载荷作用下煤岩孔隙演化特征试验研究[J]. 中国安全科学学报,2019,29(10):91−97. LI Sheng, WANG Xiaohe, FAN Chaojun, et al. Experimental study on evolution characteristics of coal pores under impact loadings[J]. China Safety Science Journal, 2019, 29(10): 91−97.
[3] 潘一山,代连朋. 煤矿冲击地压发生理论公式[J]. 煤炭学报,2021,46(3):789−799. PAN Yishan, DAI Lianpeng. Theoretical formula of rock burst in coal mines[J]. Journal of China Coal Society, 2021, 46(3): 789−799.
[4] FAN C J, LI S, LUO M K, et al. Coal and gas outburst dynamic system[J]. International Journal of Mining Science and Technology, 2017, 27(1): 49−55. doi: 10.1016/j.ijmst.2016.11.003
[5] 焦建康,鞠文君,吴拥政,等. 动载冲击地压巷道围岩稳定性多层次控制技术[J]. 煤炭科学技术,2019,47(12):10−17. JIAO Jiankang, JU Wenjun, WU Yongzheng, et al. Multi-layer control technologies for surrounding rock stability of dynamic-loading rock burst roadway[J]. Coal Science and Technology, 2019, 47(12): 10−17.
[6] 欧阳振华,易海洋,王东,等. 顶板冲击载荷作用下巷道支护体系动力响应特征研究[J]. 煤炭科技,2021,42(2):30−38. OUYANG Zhenhua, YI Haiyang, WANG Dong, et al. Numerical modeling on dynamic response of roadway supporting system induced by roof bursting waves[J]. Coal Science & Technology Magazine, 2021, 42(2): 30−38.
[7] DAI L P, PAN Y S, LI Z H, et al. Quantitative mechanism of roadway rockbursts in deep extra-thick coal seams: Theory and case histories[J]. Tunnelling and Underground Space Technology, 2021, 111: 103861. doi: 10.1016/j.tust.2021.103861
[8] 靖洪文,吴疆宇,尹乾,等. 动载扰动下深部煤巷冲击冒顶的颗粒流数值模拟研究[J]. 岩石力学与工程学报,2020,39(S2):3475−3487. JING Hongwen, WU Jiangyu, YIN Qian, et al. Particle flow simulation of rock burst and roof fall of deep coal roadway under dynamic disturbance[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(S2): 3475−3487.
[9] FAN C J, LI S, ELSWORTH D, et al. Experimental investigation on dynamic strength and energy dissipation characteristics of gas outburst-prone coal[J]. Energy Science & Engineering, 2020, 8(4): 1015−1028.
[10] 王红伟,宋远洋,焦建强,等. 大倾角煤层断层带回采巷道动载失稳机理[J]. 采矿与安全工程学报,2022,39(5):971−980. WANG Hongwei, SONG Yuanyang, JIAO Jianqiang, et al. Failure mechanism of roadway under dynamic load in fault zone of steeply inclined coal seam[J]. Journal of Mining & Safety Engineering, 2022, 39(5): 971−980.
[11] 刘冬桥,王炀,胡祥星,等. 动载诱发冲击地压巷道围岩应力计算与试验分析[J]. 煤炭科学技术,2015,43(9):42−46,116. LIU Dongqiao, WANG Yang, HU Xiangxing, et al. Calculation and test analysis on stress of surrounding rock in mine roadway with mine pressure bump occurred by dynamic load[J]. Coal Science and Technology, 2015, 43(9): 42−46,116.
[12] TANG J B, LI S, QIN G S, et al. Experiments on mechanical response and energy dissipation behavior of rockburst-prone coal samples under impact loading[J]. Shock and Vibration, 2021, 2021(1): 9924456. doi: 10.1155/2021/9924456
[13] 赵洪宝,王中伟,张欢,等. 冲击荷载对煤岩内部微结构演化及表面新生裂隙分布规律的影响[J]. 岩石力学与工程学报,2016,35(5):971−979. ZHAO Hongbao, WANG Zhongwei, ZHANG Huan, et al. Effects of dynamic loads on development of internal microstructure and distribution of new surface fractures of coal[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(5): 971−979.
[14] 刘学生,范德源,谭云亮,等. 深部动载作用下超大断面硐室群锚固围岩破坏失稳机制研究[J]. 岩土力学,2021,42(12):3407−3418. LIU Xuesheng, FAN Deyuan, TAN Yunliang, et al. Failure and instability mechanism of anchored surrounding rock for deep chamber group with super-large section under dynamic disturbances[J]. Rock and Soil Mechanics, 2021, 42(12): 3407−3418.
[15] 李夕兵,廖九波,赵国彦,等. 动力扰动下高应力巷道围岩动态响应规律[J]. 科技导报,2012,30(22):48−54. LI Xibing, LIAO Jiubo, ZHAO Guoyan, et al. Dynamic response of surrounding rock in highly-stressed tunnel under dynamic disturbance[J]. Science & Technology Review, 2012, 30(22): 48−54.
[16] 王学滨,刘桐辛,田锋,等. 周期冲击载荷下巷道顶板开裂机理数值模拟[J]. 煤炭学报,2021,46(10):3106−3115. WANG Xuebin, LIU Tongxin, TIAN Feng, et al. Numerical simulation of tunnel roof cracking mechanism under periodic impact loads[J]. Journal of China Coal Society, 2021, 46(10): 3106−3115.
[17] 肖治民,刘军,王贺,等. 动载诱发巷道底板冲击失稳机制及防控技术[J]. 地下空间与工程学报,2019,15(5):1573−1581. XIAO Zhimin, LIU Jun, WANG He, et al. Study on mechanism and control of rock burst instability of roadway floor induced by dynamic load disturbance[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(5): 1573−1581.
[18] 唐杰兵,鞠文君,焦建康,等. 矩形巷道矿震应力波扩散规律谱元法分析[J]. 中国安全生产科学技术,2021,17(9):32−38. TANG Jiebing, JU Wenjun, JIAO Jiankang, et al. Spectral element analysis on stress wave diffusion laws of mine earthquake in rectangular roadway[J]. Journal of Safety Science and Technology, 2021, 17(9): 32−38.
[19] JIA C, LI S, FAN C J, et al. Numerical simulation of mechanical characteristics of roadway surrounding rock under dynamic and static loading[J]. Shock and Vibration, 2021, 2021(1): 1869583. doi: 10.1155/2021/1869583
[20] PAN S Q, LIU S T, CAO L M, et al. Deformation failure and support test of surrounding rock in deep arched roadway with straight wall[J]. Advances in Civil Engineering, 2021, 2021(1): 3208974. doi: 10.1155/2021/3208974
[21] 孙艺丹,杨逾,孙博一,等. 动力扰动下巷道围岩变形影响因素敏感性分析[J]. 煤炭科学技术,2020,48(5):57−62. SUN Yidan, YANG Yu, SUN Boyi, et al. Sensitivity analysis of roadway surrounding rock deformation factors under dynamic disturbance[J]. Coal Science and Technology, 2020, 48(5): 57−62.
[22] 熊藤根,常聚才,史文豹,等. 不同强度动载叠加下巷道围岩力学特征数值模拟研究[J]. 矿业研究与开发,2021,41(7):118−122. XIONG Tenggen, CHANG Jucai, SHI Wenbao, et al. Numerical simulation on mechanical characteristics of roadway surrounding rock under superimposed dynamic load with different strengths[J]. Mining Research and Development, 2021, 41(7): 118−122.
[23] 孙泽权,蒋力帅,郭涛,等. 动载扰动下复合顶板巷道围岩变形破坏特征[J]. 煤炭技术,2022,41(1):13−19. SUN Zequan, JIANG Lishuai, GUO Tao, et al. Characteristics of surrounding rock deformation and failure of composite roof roadway under dynamic load disturbance[J]. Coal Technology, 2022, 41(1): 13−19.
[24] 肖海滨. 深井上山巷道底板动载诱发冲击矿压控制技术[J]. 煤炭科学技术,2017,45(4):39−44. XIAO Haibin. Control technology of mine pressure bump occurred by floor dynamic loading in rise gateways of deep mine[J]. Coal Science and Technology, 2017, 45(4): 39−44.
[25] 孙艺丹. 深部开采覆岩断裂动载下巷道围岩失稳机理及控制研究[D]. 阜新:辽宁工程技术大学,2020. SUN Yidan. Study on the mechanism and control of surrounding rock instability under the dynamic load of overburden fracture in deep mining[D]. Fuxin: Liaoning Technical University, 2020.
[26] 罗明坤,贾策,李胜,等. 基于瑞利波技术的开拓大巷地质异常超前探测研究[J]. 煤矿安全,2023,54(9):240−247. LUO Mingkun, JIA Ce, LI Sheng, et al. Study on advance detection of geological anomaly in development roadway based on Rayleigh wave technology[J]. Safety in Coal Mines, 2023, 54(9): 240−247.
计量
- 文章访问数: 17
- HTML全文浏览量: 2
- PDF下载量: 3
