Prediction of water inrush from coal seam floor based on machine learning with small sample data
-
摘要:
随着计算机技术的发展,机器学习方法已成为煤层底板突水预测的重要技术;算法预测精准度对样本的数量要求较高,制约着实际应用。运用最近邻算法(KNN)以及梯度提升决策树(GBDT)与逻辑回归(LR)结合运用的算法,基于以水压、采高、隔水层厚度、断层落差、煤层倾角、断层距工作面距离等6项指标的样本数据建立了突水预测模型,讨论了样本数量对预测精度的影响规律,并与常用的粒子群、支持向量机、BP神经网络、随机森林以及卷积神经网络进行对比研究。研究结果表明:当样本数量达到18时,KNN和GBDT+LR预测精度保持稳定;KNN与GBDT+LR在小样本条件下的预测精度高于常规预测模型;模型预测结果与实际情况相符。
Abstract:With the development of computer technology, machine learning method has become an important technology for the prediction of water inrush in coal seam floor. However, the prediction accuracy of many machine learning algorithms requires a high number of samples, which restricts the practical application. In this paper, by using the nearest neighbor algorithm (KNN) and the combination algorithm of gradient boosting decision tree (GBDT) and logistic regression (LR), a water inrush prediction model was established based on the sample data of six indexes, including water pressure, mining height, water-barrier thickness, fault drop, coal seam inclination, and fault distance from the working face. The influence rule of sample number on prediction accuracy was discussed, and the comparison study was conducted with the commonly used particle swarm, support vector machine, BP neural network, random forest and convolutional neural network. The results show that when the number of samples reaches 18, the prediction accuracy of KNN and GBDT+LR remains stable. The prediction accuracy of KNN and GBDT+LR is higher than that of conventional models under small sample conditions. The predicted results of the model agree with the actual situation.
-
承压水上采煤底板突水是我国煤炭开采中的重大灾害之一,底板突水的预测与预防一直是我国煤矿安全开采中的1项技术难题[1-4]。目前,众多学者针对底板突水问题开展了大量的研究工作,提出了多种突水危险性理论与判据,包括“突水系数”[3]、“递进导升”[5]、“板模型”[6]、“下三带”[7-8]、“关键层”[9]等,这些理论与判据对矿井安全生产起到了积极的指导作用。但由于影响煤层底板突水的因素众多,上述单纯力学、经验统计的分析方法在解决突水预测时一直得不到质的突破,因此,寻找1种能综合考虑多种因素的突水预测方法一直是煤矿突水预测的重要问题。
近年来,随着计算机技术的飞速发展,机器学习已在众多领域取得了成功应用[10],部分学者也将其引入到对煤层底板突水的预测。2015年,施龙青等[1]首先将基于粒子群算法以及支持向量机分类技术结合建立了底板突水危险性评价模型;2017年,温廷新等[11]引入了主成分分析与模糊评价的思想并运用随机森林方法对突水问题进行预测;2021年,陈建平等[12]引入卷积神经网络的思想建立煤层底板突水预测模型,运用建立的神经网络模型在影响因素及其相互联系中进行特征提取;2018年,陈桂军等[13]提出结合ε不敏感损失间隔的带负类支持向量数据描述算法的概念,使得在突水数据较少时能有较高的准确率。
综上所述,目前应用到底板突水预测中的机器学习方法主要涉及粒子群、支持向量机[14]、神经网络[15-16]以随机森林算法。但上述算法存在着迁移能力差、参数要求高、样本数量需求大的问题;而最近邻算法(KNN)[17]理论成熟、准确度高,对异常值不敏感;逻辑回归(LR)[18]训练时不同特征会对最后结果造成不同的影响,从而方便调整输出结果;GBDT[19]算法由多棵决策树组成,其预测结果由多棵树的结果相加而得,泛化能力较强。由于LR本身无法筛选特征,所以使用GBDT来筛选特征,构建GBDT与LR结合的算法。但是未见上述算法在煤层底板突水预测中应用。为此,提出通过构建KNN,GBDT与LR结合的算法模型来对煤层底板突水进行预测,分析其预测精度以及通过实例分析算法的应用效果;研究成果丰富了机器学习算法在煤层底板突水预测中的应用,可为样本数较少的情况下达到精准判断突水风险提供了理论依据。
1. 算法简介
KNN算法是1种基本的机器学习方法,该方法准确度高,受异常点的影响较小,易于实现,可以处理分类问题与回归问题;GBDT算法能处理非线性数据,在参数调整较少的情况下,模型预测的准确性仍相对较高。相对于其他算法,逻辑回归(LR)在分类过程中,计算量仅与特征数量成正比;另外,LR模型具有良好的可解释性,通过观察特征权重,可以了解各个特征对最终结果的影响程度。故此将其引入煤层底板突水预测当中。
1.1 KNN算法
KNN算法的思想是:当1个样本在给定数据集中的K个最相近的样本大多属于某个特定的类别时,该样本也将被归入这一类别。在分类时,根据几个最邻近数据的类来决定待测数据的类别。KNN算法要求对数据的所有特征进行量化处理,故在距离度量中引入期望和方差,以更准确地评估样本之间的相似度。
距离度量有3种方式:欧几里得距离(式(1))、曼哈顿距离(式(2))、闵可夫斯基距离(式(3))。欧式距离是最常用的距离度量之一,它是闵可夫斯基距离在p=2时的特例。同理,曼哈顿距离是闵可夫斯基距离在p=1时的特例。
$$ {d_1}(x,y) = \sqrt {\sum\limits_{k = 1}^n {{{({x_k} - {y_k})}^2}} } $$ (1) $$ {d_2}(x,y) = \sum\limits_{k = 1}^n {\left| {{x_k} - {y_k}} \right|} $$ (2) $$ \begin{split} &\begin{gathered} D(x, y)= \sqrt[p]{\left(\left|x_1-y_1\right|\right)^p+\left(\left|x_2-y_2\right|\right)^p+\ldots+\left(\left|x_n-y_n\right|\right)^p} =\\ \sqrt[p]{\sum_{i=1}^n\left(\mid x_i-y_i\right)^p} \end{gathered}\\ \;\\[-42pt]& \end{split} $$ (3) 式中:d1(x,y)为欧几里得距离;d2(x,y)为曼哈顿距离;D(x,y)为闵可夫斯基距离;(x,y)为样本数据在二维平面中的位置。
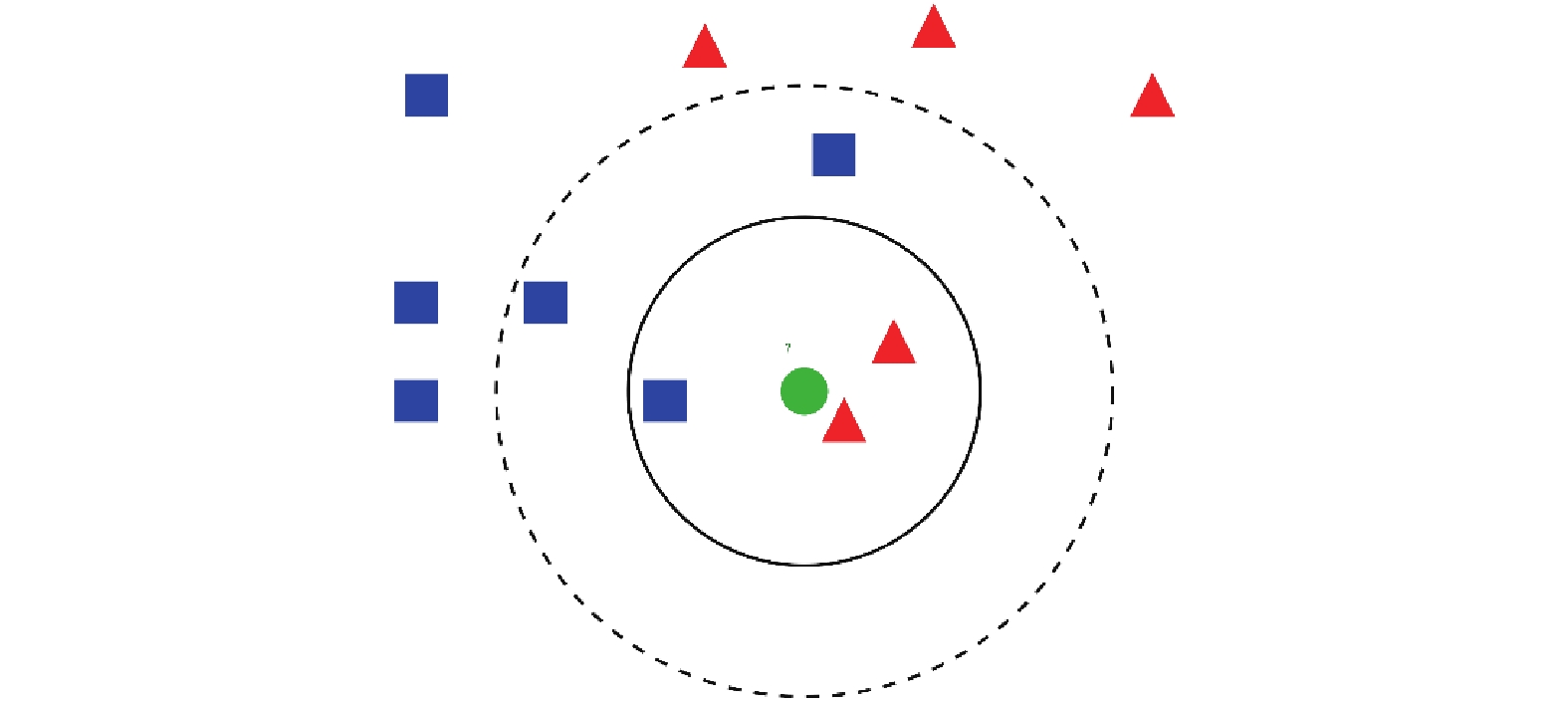
为了确定待测数据的类别,选取所有数据集中的数据作为参考,计算待测数据与所有已知数据的相似程度,从中选取与待测数据最相似的K个数据,根据少数服从多数的投票原则,将待测数据归类为K个最邻近数据中占比最高的类。KNN算法原理如图1所示。
由图1可知:要对中心的绿色圆判断赋予红色三角形与蓝色四方形其中的一类,K值的选择可以展现在实线与虚线,在K值选择为实线区域时,红色三角形在实线内所占比例为2/3,占比最高,故绿色圆被归类为红色三角形类;在K值选择为虚线区域时,蓝色四方形在虚线内占比为3/5,占比最高,因此绿色圆被赋予蓝色四方形类。
1.2 梯度提升决策树
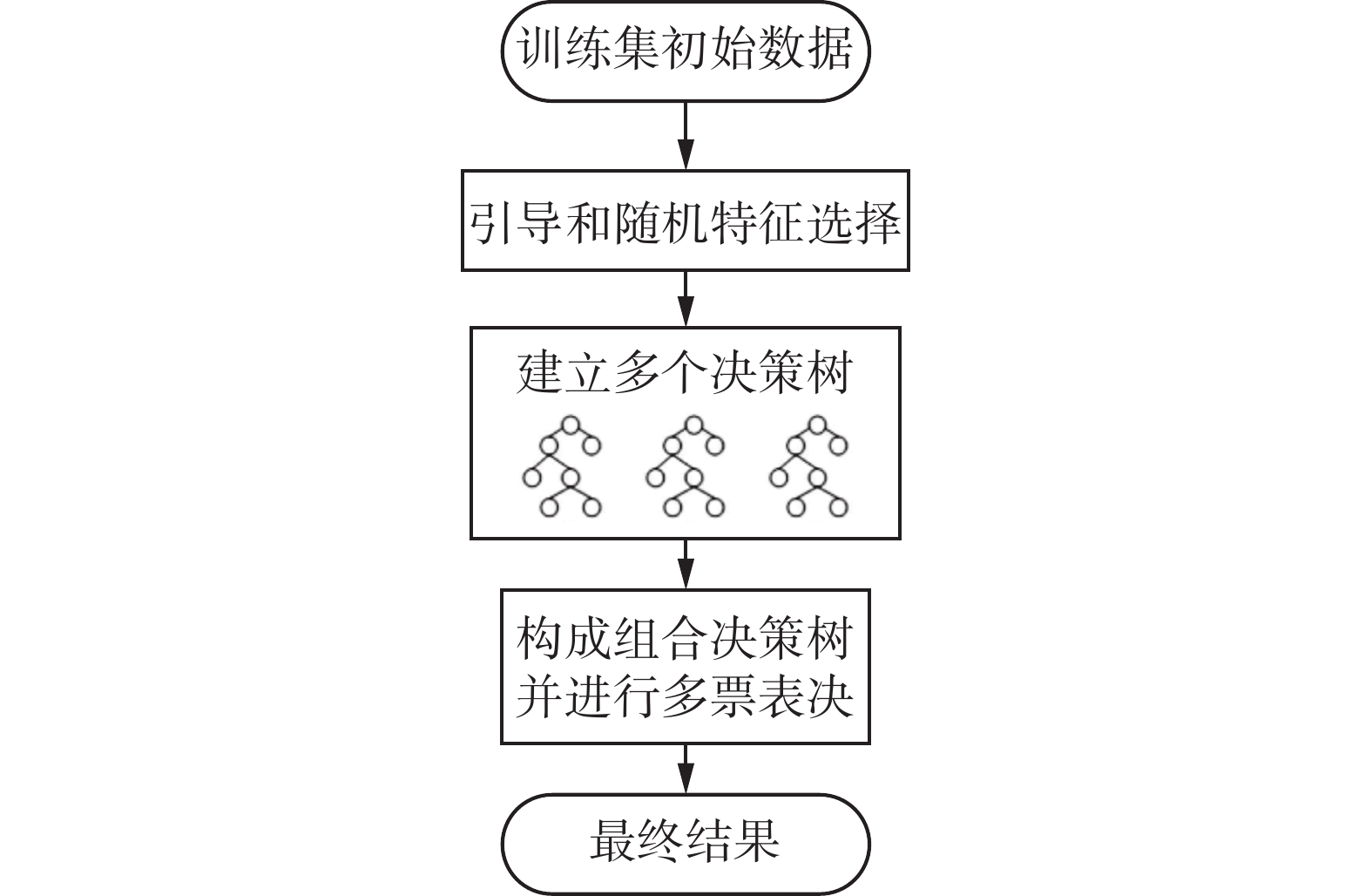
GBDT(Gradient Boosting Decision Tree)在训练过程中采用前向分步算法进行贪婪学习,这种算法通过不断地修正之前所有步骤的错误以优化模型的性能。GBDT算法流程图如图2所示。
GBDT通过对训练集初始数据进行特征选择,构建多个决策树,并进行多数票表决,从而得到最终结果。其中,每次迭代都会学习1棵决策树,将之前t−1棵树的模拟结果与实际数据之间的差距进行拟合。根据当前模型损失函数的负梯度信息训练新的弱分类器,然后将训练得到的优化弱分类器以集成方式融入现有的模型结构中。GBDT的核心思想为:每1棵树都会从上1棵树的预测结果中学习到上1棵树的预测结果与真值的残差累加,这种残差可以看作是1种累积的预测值。
模型训练过程中,对样本损失的预测尽量准确,与需要进行参数化表示的模型不同,GBDT直接在函数空间中进行定义,这样大大增加了可应用模型的种类范围,在数据挖掘、推荐系统等领域有着广泛的应用。
1.3 逻辑回归
逻辑回归(Logistic Regression)是1种用于预测分析的工具,通过解释1个或多个自变量与因变量之间的关系来进行分类。与线性回归不同,逻辑回归的目标变量具有多个类别,因此,主要应用于解决分类问题。尽管名称中包含“回归”两个字,但实际上逻辑回归是1种分类算法。核心是在线性模型之上应用Sigmoid函数,将线性模型产生的连续结果转化为离散形式。因此,逻辑回归在处理二分类问题时最为常用。
构建逻辑回归模型,主要步骤如下:
1) 寻找h函数(hypothesis);利用了Sigmoid函数,函数形式详见式(4),从式(4)中可以看出,该函数具有平滑,易于求导的特性,可以将实数映射至0和1的范围,便于处理二分类问题。
$$ g({\textit{z}})=\frac{1}{1+e^{-{\textit{z}}}} $$ (4) 式中:z为隐层神经元输出,取值范围为(0,1); g(z)为Sigmoid函数,映射范围为(0,1)。
2) 构造损失函数J(m个样本,每个样本具有n个特征)。
$$ \operatorname{Cos} {\mathrm{t}}\left(h_\theta(x), y\right)=\left\{\begin{array}{cc} -\lg \left(h_\theta(x)\right) & y=1 \\ -\lg \left(1-h_\theta(x)\right) & y=0 \end{array}\right. $$ (5) $$ \begin{split} &\begin{gathered} J(\theta)=\frac{1}{m} \sum_{i=1}^m \operatorname{Cos} {\mathrm{t}}\left(h_\theta\left(x_i\right), y_i\right) = \\ -\frac{1}{m}\left[\sum_{i=1}^m\left(y_i \lg h_\theta\left(x_i\right)+\left(1-y_i\right) \lg \left(1-h_\theta\left(x_i\right)\right)\right)\right] \end{gathered}\\[-16pt]& \end{split}$$ (6) 式中:$ \theta $为最佳参数;函数h(x)为构造的预测函数;y值0和1为2种类别;xi、yi为样本数据;Cost函数为代价函数;J函数为损失函数,帮助模型的优化。
3) 使J函数最小,并求得回归参数(θ)。
4) 在模型训练过程中,会出现过拟合的问题,使模型复杂度提升,预测能力下降。通过正则化的方法,使结构风险最小化。
2. 预测模型
2.1 煤层底板突水主控因素
煤层底板突水是由多种因素相互影响而产生的,主要受含水层、隔水层、地质构造、煤层条件以及开采方法等诸多因素的影响和控制[7]。
众所周知,煤层底板下承压含水层的存在是底板突水现象的物质基础,水压与矿压则成为底板突水的动力来源,隔水层则对底板突水起到抑制作用。隔水层的抑制能力主要取决于隔水层的厚度与强度。当其他地质条件处在一种相对平衡的状态时,断层会对底板突水起决定性作用。
这是因为断层等地质构造容易形成导水通道,破坏平衡状态;煤层倾角,采高等决定了空间位置关系,是突水事故发生的诱因,会直接影响隔水层从而破坏平衡。因此,选择含水层水压,采高,隔水层厚度,断层落差,煤层倾角,断层距工作面距离这6项作为特征值,来进行突水预测模型的构建与测试。
2.2 基于KNN算法的模型
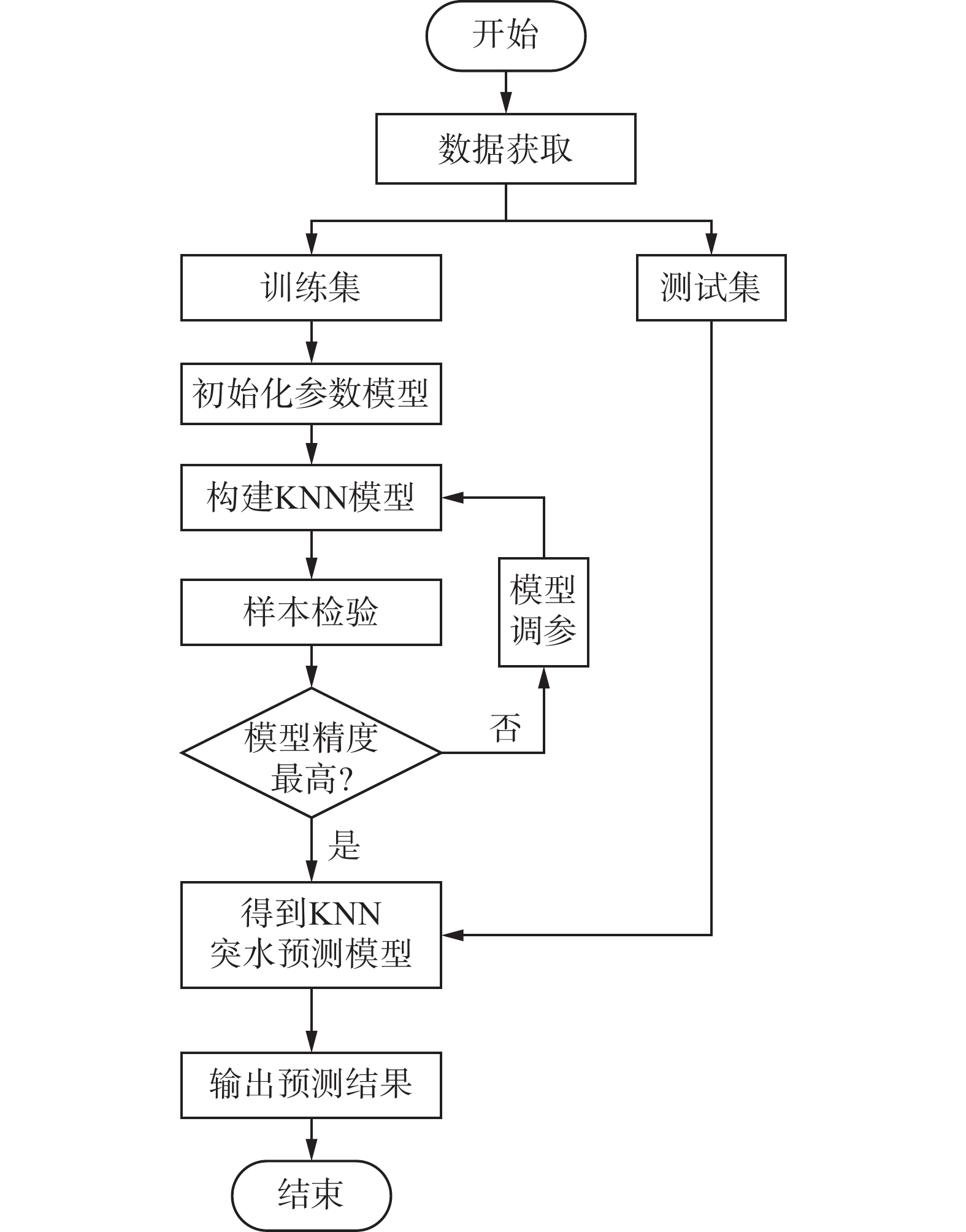
从煤层底板突水相关数据中选取突水数据与正常数据作为训练集,构建KNN算法模型。KNN算法模型建立如图3所示。
KNN算法的详细步骤为:①计算当前点与数据集中的点距离的大小;②按照距离递增次序排序;③选取与当前点距离最小的K个点;④确定前K个数据点,并确定它们所在类别的分布;⑤预测当前点的分类在前K个点中出现频率最高的类别。
2.3 基于GBDT+LR算法的模型
GBDT弱分类器要求不高,所构建的树层数相对较少;该方法无需进行特征标准化处理,数据集中可存在部分缺失的数据;可以自动组合多个特征,并能自动处理特征间的交互,不用担心数据是否具有线性可分性;同时能够灵活处理多种类型的异构数据,对异常值有一定的鲁棒性。LR模型具有简洁的形式,良好的可解释性,较低的资源占用,并且可以根据特征的权重来反映不同特征对预测结果的影响。训练过程易于并行化,可以防止信息损失,在实际的应用中保留存储权重比较大的特征及对应的权重就可保证有较好的预测精度。
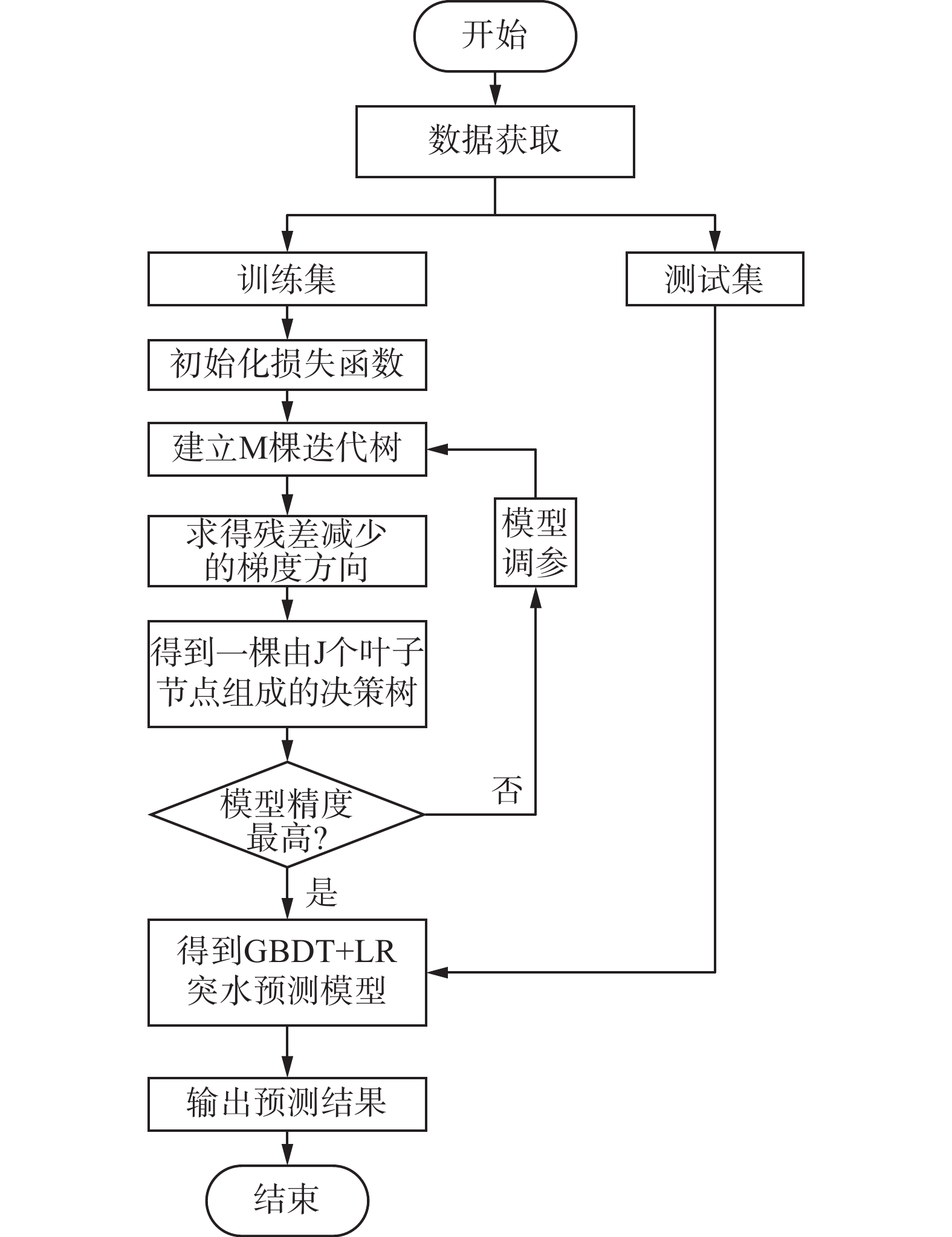
LR也存在一些局限性,例如其表达能力较弱,无法有效处理特征交叉,准确率并不是很高以及很难去拟合数据的真实分布。在考虑了GBDT和LR的优缺点后,提出了构建1种GBDT与LR结合的预测模型来对煤层底板突水进行预测。该模型首先运用GBDT进行特征选择,随后,将特征向量输入LR模型当中,构建突水预测模型。这种算法可以拟合更加复杂的函数,拥有更强的模型表达能力。GBDT+LR算法模型建立如图4所示。
构建GBDT模型的过程和主要步骤为:
1)模型初始化,输入训练集与损失函数。选择Huber损失函数L(y,f(x))。Huber损失函数是均方差(MSE)和平均绝对误差(MAE)的折中产物,均方差光滑连续、可导,但是容易受到异常数据的影响;平均绝对误差呈“V”形,受异常数据影响较小,但梯度较大,不利于函数的收敛;而Huber损失函数通过δ值的大小决定对 MSE 和 MAE 的侧重性。Huber损失函数同时具备了 MSE 和 MAE 的优点,减少了受异常数据影响的问题,实现了处处可导。对于靠近中心的异常点,通常采用平方损失,而对于远离中心的点则采用绝对损失。这种分界点的选择通常通过分位数点来进行度量,以此来实现不同类型数据损失的均衡,Huber损失函数的表达式:
$$ L(y, f(x))=\left\{\begin{array}{cc} \dfrac{1}{2}(y-f(x))^2 & |y-f(x)| \leqslant \delta \\ \delta\left(|y-f(x)|-\dfrac{\delta}{2}\right) & |y-f(x)|>\delta \end{array}\right. $$ (7) 式中:δ为超参数;y为样本数据真实值;f(x)为预测值;L为损失函数。
2) 对于第m轮迭代,计算残差$ r_{m} $,如式(8)计算损失函数在当前模型的值为残差。
$$ r_{m w}=-\left[\frac{\partial L\left(y_i, f\left(x_i\right)\right)}{\partial f\left(x_i\right)}\right]_{f(x)-f_{m-1}(x)} $$ (8) 式中:$ r_{m} $为残差;m为迭代次数。
3) 完成模型构建,并进行测试,查看模型的精确度。
3. 实验结果
本次机器学习所需样本数据来源于文献[1]中所列出的部分华北型煤田煤层底板突水典型案例,结合KNN算法,GBDT算法与逻辑回归的原理,利用python中的scikit-learn库实现模型的建立,对算法模型进行训练。训练数据见表1。
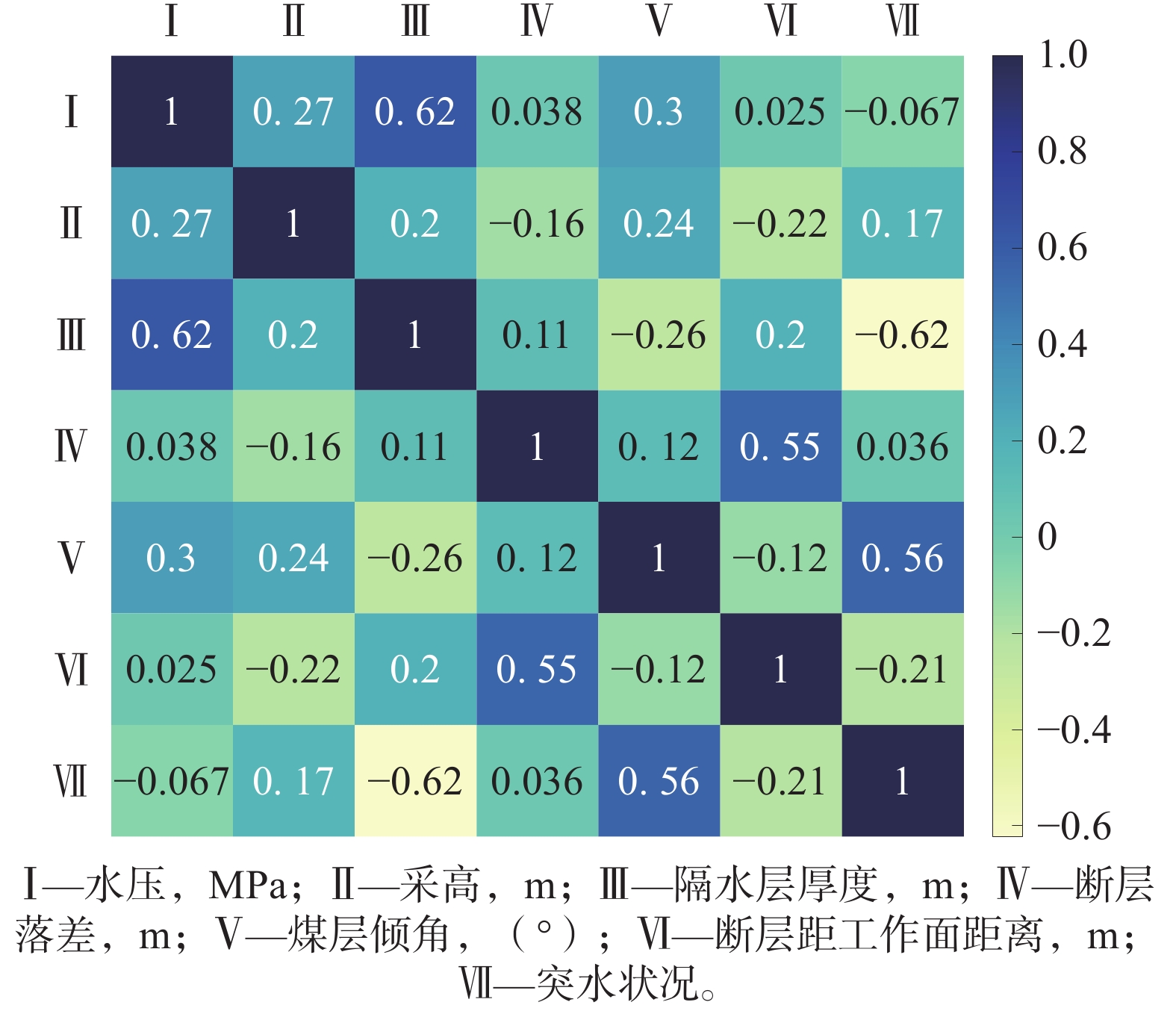
表 1 训练数据Table 1. Training data名称 水压/MPa 采高/m 隔水层厚度/m 断层落差/m 煤层倾角/(º) 断层距工作面距离/m 突水状况 夏庄煤矿 1.82 0.80 26.39 4.00 12 16 是 夏庄煤矿 1.65 1.60 25.85 50.00 17 90 是 夏庄煤矿 1.00 0.90 22.33 2.00 13 16 是 夏庄煤矿 2.88 1.00 17.68 1.30 20 0 是 井陉三煤矿 2.01 8.00 28.00 0.60 18 10 是 井陉三煤矿 1.91 8.00 43.00 1.50 11 2 是 洪山煤矿 1.33 0.85 36.38 0.80 7 62 否 洪山煤矿 0.95 1.45 26.89 1.00 6 55 否 洪山煤矿 0.92 1.40 33.61 0.50 8 0 否 洪山煤矿 0.34 0.90 32.65 22.00 6 6 否 黑山煤矿 1.06 2.00 27.79 0.46 7 21 否 黑山煤矿 0.83 2.85 26.56 0.70 12 6 否 谢一矿33采区底板 2.00 2.81 30.00 1.50 18 12 是 九里山煤矿12031工作面 1.80 1.90 23.00 0 15 17 是 潘东井106工作面 1.70 2.80 10.00 5.00 17 10 是 肥城陶阳煤矿9901工作面 0.60 1.10 17.00 8.00 19 6 是 华泰351504工作面 2.10 1.60 59.50 3.50 10 39 否 潘西6197工作面 2.80 2.75 69.17 11.70 12 36 否 潘西6196工作面 2.80 2.55 66.11 16.00 12 29 否 新汶协庄煤矿31104工作面 1.30 1.70 30.00 4.90 5 21 是 获得数据后,通过对数据进行探索,可以了解其基本结构、获取关键统计信息、评估数据噪声以及观察数据分布等。对数据进行预处理,对特征值(前6项)和目标值(第7项)确定,将数据集进行分割,绘制数据的热力图。数据热力图如图5所示。
从图5中可以看出数据间存在的关系,煤层底板突水的标签与隔水层的厚度负相关系数较大,说明隔水层厚度较大时不易出现煤层底板突水;而与煤层倾角正相关系数较大,则体现煤层倾角较高时,有可能出现煤层底板突水。
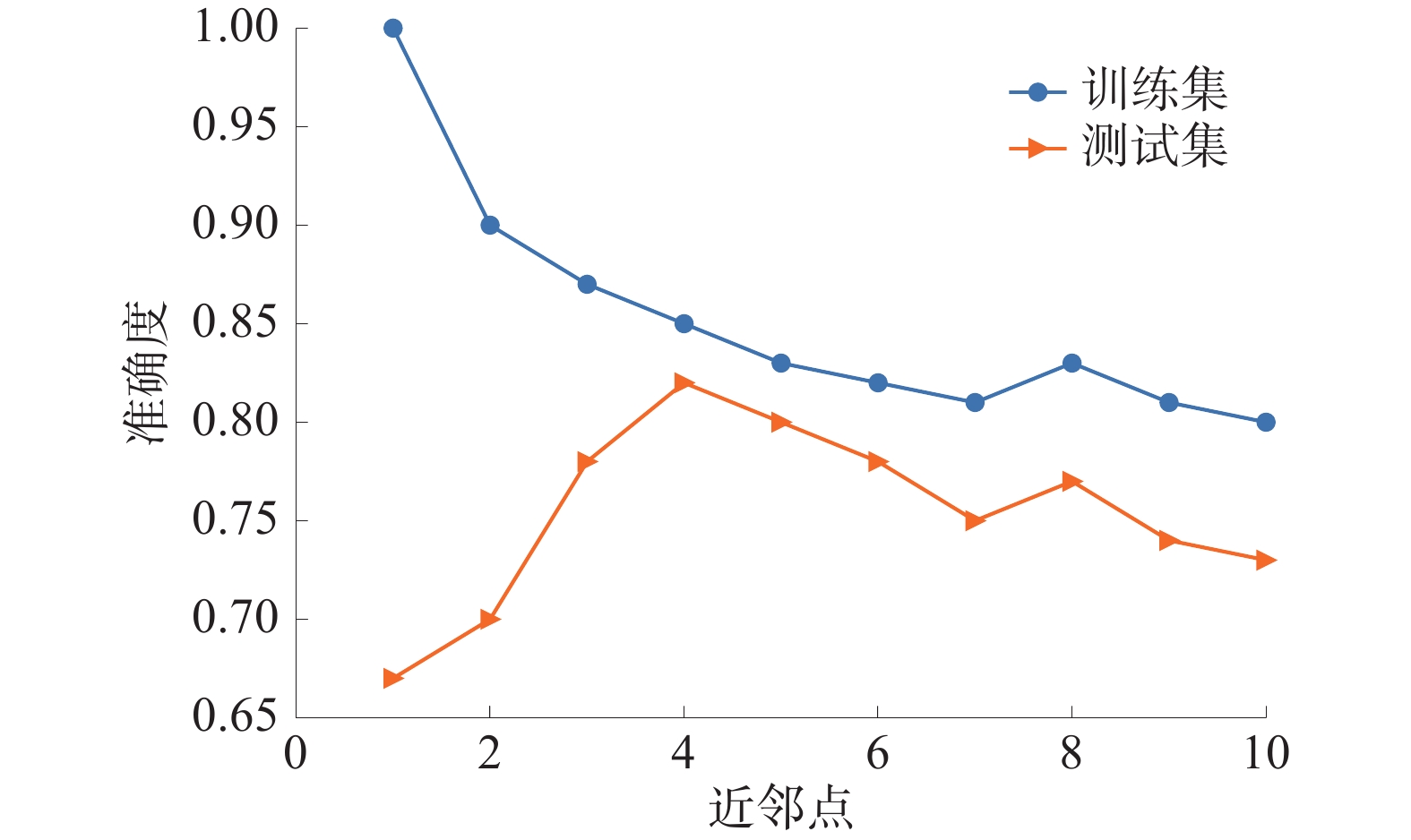
模型训练过程中,对模型相关参数进行调节。基于GBDT+LR实现煤层底板突水预测过程中,LR算法也可以从特征的权重可以了解不同的特征对最终结果的影响程度,隔水层厚度,煤层倾角等对突水影响较大,通过调整弱学习器个数,迭代次数与损失函数构建模型,使得能够较为精准地预测;在基于KNN算法实现煤层底板突水预测过程中,预测精准度很大程度上取决于K值。在代码中,通过建立循环遍历来寻找合适的K值。不同K值对应数据集与测试集的准确率如图6所示。
由图6可以看出:训练集和测试集在模型预测准确度和近邻点之间的关系;当K=1时,训练集的预测是正确的,随着近邻点的增加,训练集的准确度下降,而测试集的准确度上升并有所波动;当K=4时,准确度最为接近,因此选择K=4为最佳参数。
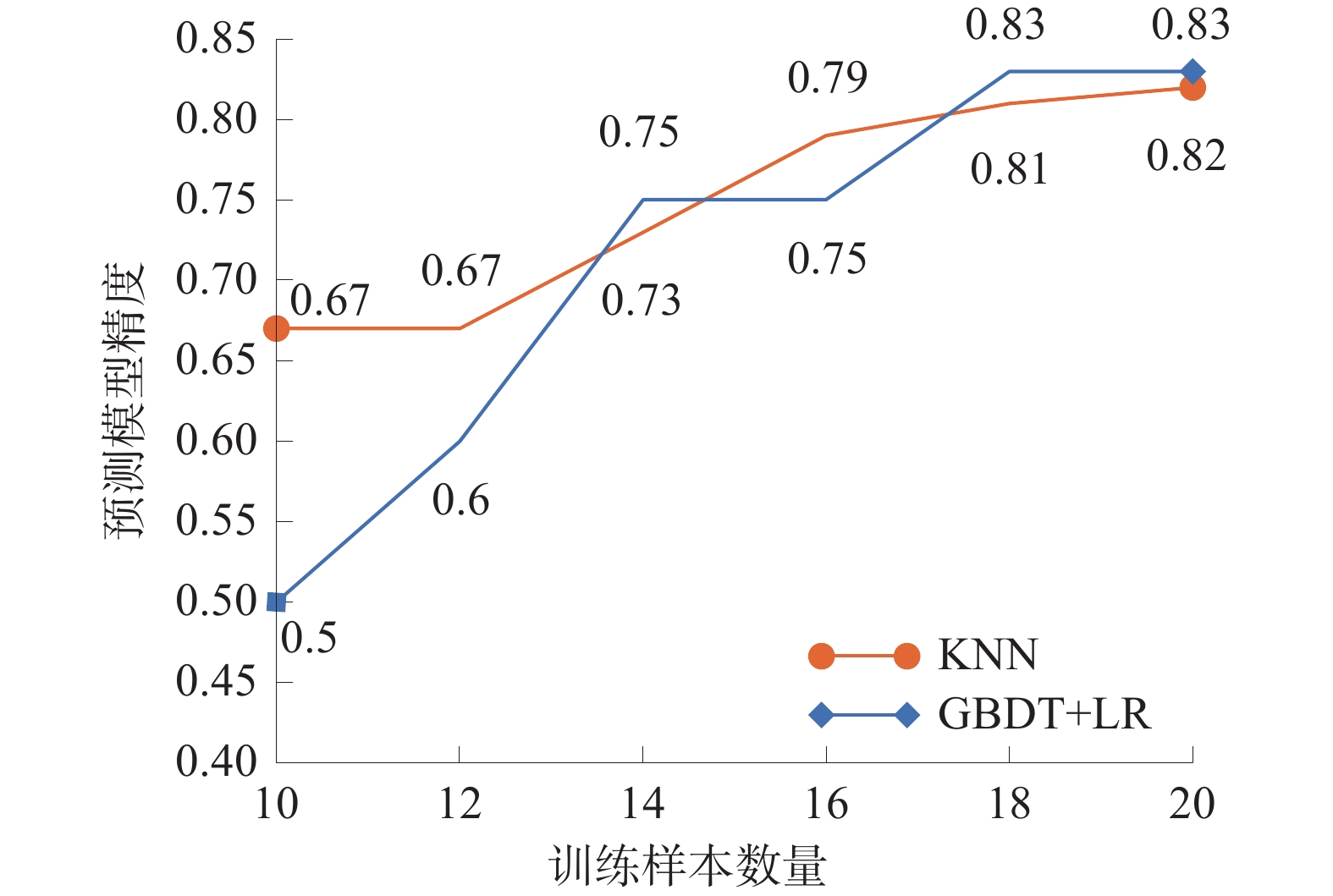
在建立突水预测模型时,样本数据的选择对模型的准确性和稳定性具有重要影响,将训练数据分别取前10项、12项、14项、16项、18项、20项构建突水预测模型。通过运用KNN和GBDT+LR2种算法构建突水预测模型,样本数据精度图如图7所示。
由图7可知:随着样本数量的增加,模型精度逐渐提高;当样本数量达到18个以后,模型精度趋于稳定,说明在一定范围内,增加样本数量可以提高模型精度;但当样本数量达到一定阈值后,模型精度趋于稳定。考虑到模型稳定性和预测精度的重要性,选择了20个样本作为训练数据。这样可以确保模型具有足够的样本信息来捕捉突水的规律和特征,同时保证模型的稳定性和准确性。
虽然 KNN 算法和 GBDT+LR 算法并不是专门为小样本数据设计的机器学习方法,但在小样本情况下仍然可以表现出较好的效果。为了测试KNN算法受到异常值的影响,在训练数据中加入了明显有误的数据如:(0、0、0、0、0、0、0)和(99、99、99、99、99、99、99),经测试,算法训练并未受到明显影响。将训练集进行一定调整,减少部分训练集的数据,发现KNN模型有较大的波动,需要对参数进行再次调节。尽管KNN算法对异常值不敏感,但对训练集要求较高,受训练集影响较大,模型迁移困难,在模型推广应用难度较高,缺少普适性。
为了检验GBDT+LR与KNN算法在数据集训练下的精确程度,通过使用20条数据,使用支持向量机(SVM)、粒子群优化(PSO_SVM)、神经网络(BPnet)、随机森林(RF)、卷积神经网络(CNN)等不同的算法构建煤层底板突水预测模型。其中,SVM准确度为0.8;PSO_SVM准确度为0.82;BPnet准确度为0.71;RF准确度为0.75;CNN准确度为0.7;KNN准确度为0.82,GBDT+LR准确度为0.83。
在7种不同的算法中,GBDT+LR与KNN算法的准确率分别达到了0.83与0.82,在7种底板突水预测模型当中精确度较高,一定程度上说明了GBDT+LR与KNN算法能够给出更高的底板突水预测准确率。
为了进一步说明KNN算法与GBDT+LR算法在突水预测模型上的优势,以5条待预测数据作为测试数据,对7种突水预测模型进行测试。测试数据见表2,测试结果见表3。
表 2 测试数据Table 2. Test data名称 水压/MPa 采高/m 隔水层厚度/m 断层落差/m 煤层倾角/(º) 断层距工作面距离/m 突水状况 华泰31503 1.08 0.90 16.50 3.2 7 7 是 良庄51302 1.10 1.60 20.00 15.0 11 16 是 潘西6194 4.06 2.75 65.86 10.0 10 11 否 白庄9602 3.11 2.61 44.30 3.5 11 12 是 华恒61106 2.70 2.55 66.97 16.0 12 31 否 表 3 测试结果Table 3. Test results名称 SVM PSO_SVM BPnet RF CNN KNN GBDT+LR 实际情况 华泰31503 未突水 未突水 突水 未突水 未突水 突水 突水 突水 良庄51302 突水 突水 突水 突水 未突水 突水 突水 突水 潘西6194 未突水 未突水 突水 未突水 未突水 未突水 未突水 未突水 白庄9602 未突水 突水 突水 未突水 未突水 突水 突水 突水 华恒61106 未突水 未突水 未突水 未突水 未突水 未突水 未突水 未突水 正确率 0.6 0.8 0.8 0.6 0.4 1 1 1 这些机器学习算法对新数据的适应能力即泛化能力的测试结果显示:粒子群、支持向量机、BP神经网络、随机森林、卷积神经网络均有测试数据预测错误;其中,由于训练样本较少,卷积神经网络预测效果不好,而KNN算法与GBDT+LR算法全部预测正确,在实际突水预测中,对于在突水相关数据较少的情况下,基于KNN算法与GBDT+LR算法的预测方法有较强的泛化能力,具有一定优势。
4. 实例应用
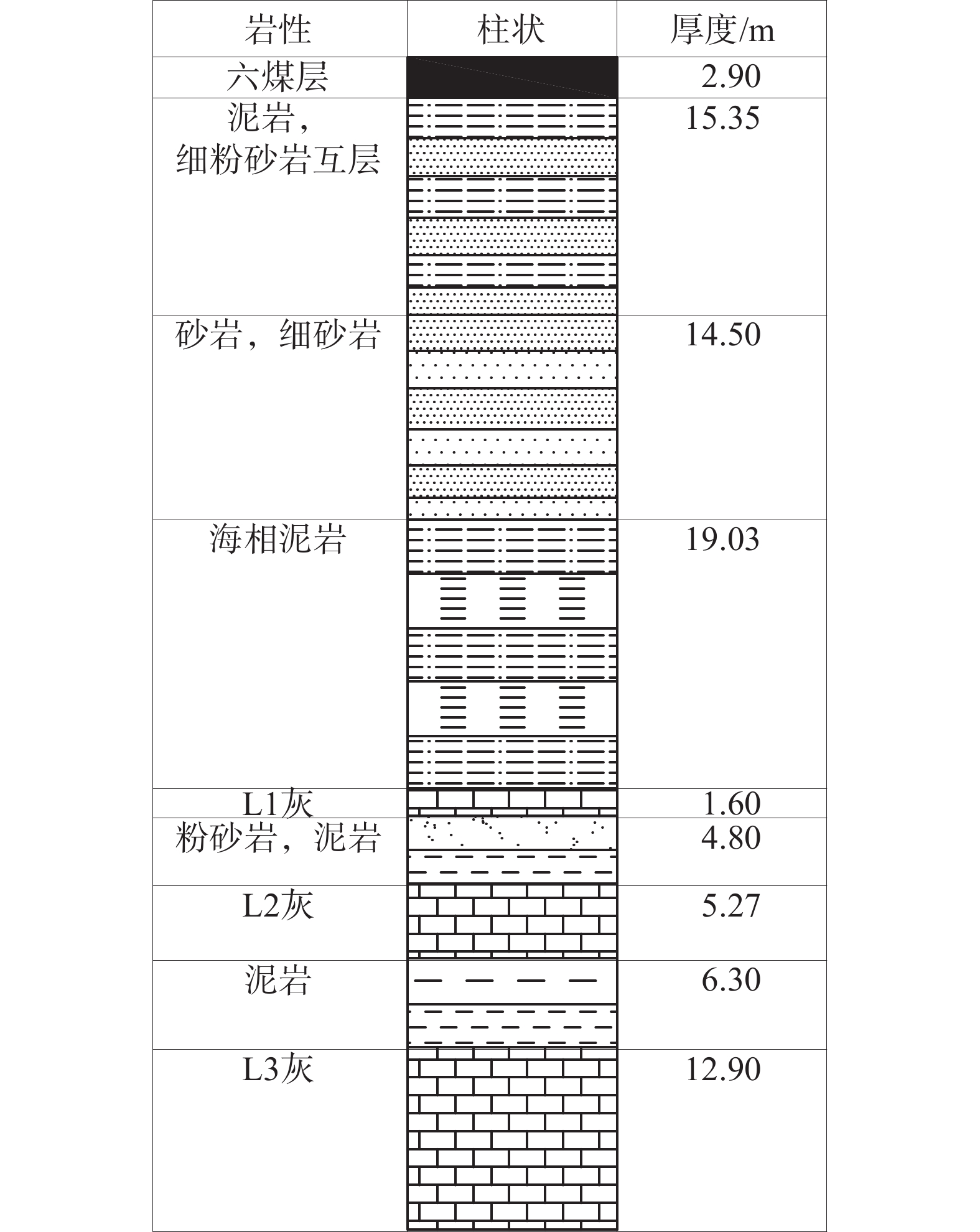
以皖北煤电集团刘桥二矿2614工作面突水预测为例,该面位于261 采区中上部东侧,主采6煤层,平均埋深470 m,工作面走向长733 m,倾向宽130~190 m,平均煤厚度2.93 m;煤层倾角为6°~11°。钻孔揭露底板隔水层的厚度为38~58 m,平均42 m,含水层水压为3.93 MPa[20]。工作面底板柱状图如图8所示。
工作面存在着落差分别为10 m和7 m的正断层,突水系数为0.093。工作面构造复杂,存在着突水的危险,采用KNN与GBDT+LR的方法对底板突水进行预测,并检验其预测的精确性。经预测,发现可能存在突水风险,与突水系数判定取得一致,而当采用支持向量机(SVM)、粒子群优化(PSO_SVM)、神经网络(BPnet)、随机森林(RF)、卷积神经网络(CNN)时,预测结果分别显示突水、突水、未突水、未突水、未突水,部分算法与突水系数判定相差较大。通过疏水降压与注浆加固后,降深60 m,工作面突水系数不大于0.07,突水风险较小;将疏水降压后的数据导入采用GBDT+LR与KNN的突水预测模型后,预测无突水情况,与突水系数法判定效果相符。目前工作面已安全回采,无突水危险性。显示了GBDT+LR与KNN的方法在底板突水预测上的准确性。研究内容实现了基于小样本数据的突水危险的精准判定,为水害防治的预测预报提供了重要的理论支撑。
5. 结 语
1)选择水压、采高、隔水层厚度、断层落差、煤层倾角、断层距工作面距离6项因素作为特征值,基于较少样本数据运用KNN和GBDT+LR的机器学习方法实现对煤层底板突水的预测。
2)样本数量对机器学习算法的预测精度有重要影响,当样本数量达到18时,KNN和GBDT+LR预测精度趋于稳定。
3)运用KNN算法对突水问题进行预测,通过K值的选择可得到较高的精确度。但是受训练集影响较大,模型迁移困难。运用GBDT+LR算法对突水问题进行预测,解决了LR本身无法筛选特征,可以增加模型的鲁棒性,模型的表达能力更强。
4)与常用的粒子群、支持向量机、BP神经网络、随机森林以及卷积神经网络相比,可能会受到样本数量的限制,导致预测精度受到一定影响。而KNN和GBDT+LR算法在一定程度上能够克服这种限制,即使在样本数量较少的情况下,也能够实现较高的预测精度。
5)实例应用结果表明,提出的基于小样本数据下的突水预测机器学习模型判定结果与实际情况相符;研究成果可为煤矿水害防治提供一定的借鉴。
-
表 1 训练数据
Table 1 Training data
名称 水压/MPa 采高/m 隔水层厚度/m 断层落差/m 煤层倾角/(º) 断层距工作面距离/m 突水状况 夏庄煤矿 1.82 0.80 26.39 4.00 12 16 是 夏庄煤矿 1.65 1.60 25.85 50.00 17 90 是 夏庄煤矿 1.00 0.90 22.33 2.00 13 16 是 夏庄煤矿 2.88 1.00 17.68 1.30 20 0 是 井陉三煤矿 2.01 8.00 28.00 0.60 18 10 是 井陉三煤矿 1.91 8.00 43.00 1.50 11 2 是 洪山煤矿 1.33 0.85 36.38 0.80 7 62 否 洪山煤矿 0.95 1.45 26.89 1.00 6 55 否 洪山煤矿 0.92 1.40 33.61 0.50 8 0 否 洪山煤矿 0.34 0.90 32.65 22.00 6 6 否 黑山煤矿 1.06 2.00 27.79 0.46 7 21 否 黑山煤矿 0.83 2.85 26.56 0.70 12 6 否 谢一矿33采区底板 2.00 2.81 30.00 1.50 18 12 是 九里山煤矿12031工作面 1.80 1.90 23.00 0 15 17 是 潘东井106工作面 1.70 2.80 10.00 5.00 17 10 是 肥城陶阳煤矿9901工作面 0.60 1.10 17.00 8.00 19 6 是 华泰351504工作面 2.10 1.60 59.50 3.50 10 39 否 潘西6197工作面 2.80 2.75 69.17 11.70 12 36 否 潘西6196工作面 2.80 2.55 66.11 16.00 12 29 否 新汶协庄煤矿31104工作面 1.30 1.70 30.00 4.90 5 21 是 表 2 测试数据
Table 2 Test data
名称 水压/MPa 采高/m 隔水层厚度/m 断层落差/m 煤层倾角/(º) 断层距工作面距离/m 突水状况 华泰31503 1.08 0.90 16.50 3.2 7 7 是 良庄51302 1.10 1.60 20.00 15.0 11 16 是 潘西6194 4.06 2.75 65.86 10.0 10 11 否 白庄9602 3.11 2.61 44.30 3.5 11 12 是 华恒61106 2.70 2.55 66.97 16.0 12 31 否 表 3 测试结果
Table 3 Test results
名称 SVM PSO_SVM BPnet RF CNN KNN GBDT+LR 实际情况 华泰31503 未突水 未突水 突水 未突水 未突水 突水 突水 突水 良庄51302 突水 突水 突水 突水 未突水 突水 突水 突水 潘西6194 未突水 未突水 突水 未突水 未突水 未突水 未突水 未突水 白庄9602 未突水 突水 突水 未突水 未突水 突水 突水 突水 华恒61106 未突水 未突水 未突水 未突水 未突水 未突水 未突水 未突水 正确率 0.6 0.8 0.8 0.6 0.4 1 1 1 -
[1] 施龙青,谭希鹏,王娟,等. 基于PCA_Fuzzy_PSO_SVC的底板突水危险性评价[J]. 煤炭学报,2015,40(1):167−171. SHI Longqing, TAN Xipeng, WANG Juan, et al. Risk assessment of water inrush based on PCA_Fuzzy_PSO_SVC[J]. Journal of China Coal Society, 2015, 40(1): 167−171.
[2] WU Q, WANG M, WU X. Investigations of groundwater bursting into coal mine seam floors from fault zones[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(4): 557−571. doi: 10.1016/j.ijrmms.2003.01.004
[3] 李忠建,魏久传,郭建斌,等. 运用突水系数法和模糊聚类法综合评价煤层底板突水危险性[J]. 矿业安全与环保,2010,37(1):24−26. doi: 10.3969/j.issn.1008-4495.2010.01.009 LI Zhongjian, WEI Jiuchuan, GUO Jianbin, et al. Comprehensive evaluation of water-inrush risk from coal floor by both water-inrush coefficientand fuzzy cluster methods[J]. Mining Safety & Environmental Protection, 2010, 37(1): 24−26. doi: 10.3969/j.issn.1008-4495.2010.01.009
[4] 李飞,孔德中,汪洋,等. 我国煤层底板突水机理与防治研究现状及展望[J]. 煤矿安全,2022,53(11):200−206. LI Fei, KONG Dezhong, WANG Yang, et al. Research status and prospect of water inrush mechanism and prevention of coal seam floor in China[J]. Safety in Coal Mines, 2022, 53(11): 200−206.
[5] 王进尚,姚多喜,黄浩. 煤矿隐伏断层递进导升突水的临界判据及物理模拟研究[J]. 煤炭学报,2018,43(7):2014−2020. WANG Jinshang, YAO Duoxi, HUANG Hao. Critical criterion and physical simulation research on progressive ascending water inrush in hidden faults of coal mines[J]. Journal of China Coal Society, 2018, 43(7): 2014−2020.
[6] ZHANG J C. Investigations of water inrushes from aquifers under coal seams[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3): 350−360. doi: 10.1016/j.ijrmms.2004.11.010
[7] 李白英. 预防矿井底板突水的“下三带”理论及其发展与应用[J]. 山东矿业学院学报(自然科学版),1999(4):11−18. LI Baiying. “Down Three Zones” in the prediction of the water inrush from coalbed floor aquifer theory, development and application[J]. Journal of Shandong Mining Institute(Natural Science Edition), 1999(4): 11−18.
[8] 李万军,杨家兵. “下三带”理论和“P-h”临界曲线法预测底板突水[J]. 煤矿开采,2010,15(5):45−47. doi: 10.3969/j.issn.1006-6225.2010.05.016 LI Wanjun, YANG Jiabing. “Down 3 zones” theory and “P-h” critical curve method for floor water-bursting forecast[J]. Coal Mining Technologg Technology, 2010, 15(5): 45−47. doi: 10.3969/j.issn.1006-6225.2010.05.016
[9] 钱鸣高,缪协兴,许家林. 岩层控制的关键层理论[M]. 徐州:中国矿业大学出版社,2000. [10] 周永章,王俊,左仁广,等. 地质领域机器学习、深度学习及实现语言[J]. 岩石学报,2018,34(11):3173−3178. ZHOU Yongzhang, WANG Jun, ZUO Renguang, et al. Machine learning, deep learning and Python language in field of geology[J]. Acta Petrologica Sinica, 2018, 34(11): 3173−3178.
[11] 温廷新,孙雪,田洪斌,等. 基于PCA_Fuzzy_RF模型的煤层底板突水预测[J]. 安全与环境学报,2017,17(3):855−858. WEN Tingxin, SUN Xue, TIAN Hongbin, et al. Prediction of the water inrush from the coal seam based on PCA_Fuzzy_ RF model[J]. Journal of Safety and Environment, 2017, 17(3): 855−858.
[12] 陈建平,王春雷,王雪冬. 基于CNN神经网络的煤层底板突水预测[J]. 中国地质灾害与防治学报,2021,32(1):50−57. CHEN Jianping, WANG Chunlei, WANG Xuedong. Coal mine floor water inrush prediction based on CNN neural network[J]. The Chinese Journal of Geological Hazard and Control, 2021, 32(1): 50−57.
[13] 陈桂军,张雪英,李凤莲,等. 基于εN-SVDD算法的煤层底板突水危险性预测[J]. 辽宁工程技术大学学报(自然科学版),2018,37(1):21−26. doi: 10.11956/j.issn.1008-0562.2018.01.004 CHEN Guijun, ZHANG Xueying, LI Fenglian, et al. Risk prediction of water inrush from coal floor based on the εN-SVDD algorithm[J]. Journal of Liaoning Technical University (Natural Science), 2018, 37(1): 21−26. doi: 10.11956/j.issn.1008-0562.2018.01.004
[14] 曹庆奎,赵斐. 基于模糊−支持向量机的煤层底板突水危险性评价[J]. 煤炭学报,2011,36(4):633−637. CAO Qingkui, ZHAO Fei. Risk evaluation of water inrush from coal floor based on fuzzy-support vector machine[J]. Journal of China Coal Society, 2011, 36(4): 633−637.
[15] 杨志磊,孟祥瑞,王向前,等. 基于GA-BP网络模型的煤矿底板突水非线性预测评价[J]. 煤矿安全,2013,44(2):36−39. YANG Zhilei, MENG Xiangrui, WANG Xiangqian, et al. Nonlinear prediction and evaluation of coal mine floor water inrush based on GA-BP neural network model[J]. Safety in Coal Mines, 2013, 44(2): 36−39.
[16] 尹会永,周鑫龙,郎宁,等. 基于SSA优化的GA-BP神经网络煤层底板突水预测模型与应用[J]. 煤田地质与勘探,2021,49(6):175−185. YIN Huiyong, ZHOU Xinlong, LANG Ning, et al. Prediction model of water inrush from coal floor based on GA-BP neural network optimized by SSA and its application[J]. Coal Geology & Exploration, 2021, 49(6): 175−185.
[17] 赵玲,陈磊琛,余小陆,等. SVM-KNN分类算法研究[J]. 计算机与数字工程,2010,38(6):29−31. doi: 10.3969/j.issn.1672-9722.2010.06.009 ZHAO Ling, CHEN Leichen, YU Xiaolu, et al. Study on SVM-KNN classification algorithm[J]. Computer & Digital Engineering, 2010, 38(6): 29−31. doi: 10.3969/j.issn.1672-9722.2010.06.009
[18] 阎馨,吴书文,屠乃威,等. 基于逻辑回归和增强学习的煤与瓦斯突出预测[J]. 控制工程,2021,28(10):1983−1988. YAN Xin, WU Shuwen, TU Naiwei, et al. Prediction of coal and gas outburst based on logistic regression and reinforcement learning[J]. Control Engineering of China, 2021, 28(10): 1983−1988.
[19] 张凌凡,陈忠辉,周天白,等. 基于梯度提升决策树的露天矿边坡多源信息融合与稳定性预测[J]. 煤炭学报,2020,45(S1):173−180. ZHANG Lingfan, CHEN Zhonghui, ZHOU Tianbai, et al. Multi-source information fusion and stability prediction of slope based on gradient boosting decision tree[J]. Journal of China Coal Society, 2020, 45(S1): 173−180.
[20] 魏大勇. 优化疏降方案在刘桥二矿工作面水害防治中的应用[J]. 华北科技学院学报,2006,3(2):5−8. doi: 10.3969/j.issn.1672-7169.2006.02.002 WEI Dayong. Application of the optimum discharge procedure to groundwater hazard control in the work face in Liuqiao coal mine[J]. Journal of North China Institute of Science and Technology, 2006, 3(2): 5−8. doi: 10.3969/j.issn.1672-7169.2006.02.002



 下载:
下载: