Risk assessment of gas explosion based on fuzzy Bayesian network improved by entropy weight method
-
摘要:
为了准确有效评估煤矿瓦斯爆炸风险,提出了基于熵权法改进的模糊贝叶斯网络瓦斯爆炸风险评估模型。首先,对瓦斯爆炸事故案例进行风险识别,提取出18个瓦斯爆炸主要风险因素;其次通过故障树模型,并根据映射规则建立出相应的贝叶斯网络模型;为减少专家判断的主观性,将熵权法结合模糊理论得到的组合权重作为贝叶斯网络的先验概率,然后通过此模型对贵州松林煤矿的瓦斯爆炸危险性进行了评估。结果表明:贵州松林煤矿瓦斯爆炸风险概率为25%,风险等级为一般风险;瓦斯积聚和煤炭自燃是导致瓦斯爆炸的主要风险因素;其中,通风阻力、瓦斯突出、防爆设备故障、违规爆破、煤自燃等因素是瓦斯爆炸的关键致因因素,评价结果与实际情况相符。
Abstract:In order to accurately and effectively evaluate the risk of gas explosion in coal mines, an improved fuzzy Bayesian network gas explosion risk assessment model based on entropy weight method is proposed. Firstly, the risk identification of gas explosion accident cases is carried out, and 18 main risk factors of gas explosion are extracted. Secondly, the fault tree model is established, and the corresponding Bayesian network model is established according to the mapping rules. In order to reduce the subjectivity of expert judgment, the combination weight obtained by entropy weight method combined with fuzzy theory is taken as the prior probability of Bayesian network, and then the risk of gas explosion in Songlin Coal Mine of Guizhou Province is evaluated by this model. The results show that the risk probability of gas explosion in Songlin Coal Mine in Guizhou is 25 %, and the risk level is general risk. Gas accumulation and coal spontaneous combustion are the main risk factors of gas explosion. Among them, ventilation resistance, gas outburst, explosion-proof equipment failure, illegal blasting, coal spontaneous combustion and other factors are the key causes of gas explosion, and the evaluation results are consistent with the actual situation.
-
Keywords:
- gas explosion /
- risk assessment /
- fault tree /
- fuzzy theory /
- entropy weight method /
- Bayesian network
-
煤炭是我国的主要能源供应,在满足能源需求方面起着主导作用[1]。瓦斯爆炸具有危险源分布广、潜伏性、突发性等诸多因素的特点[2]。当瓦斯浓度达到爆炸极限时,一旦遇到氧气和火源就会发生瓦斯爆炸,对人员和矿井造成严重危害。因此有必要对瓦斯爆炸事故进行风险识别,并对瓦斯爆炸事故的风险进行定量评估,从而预防瓦斯爆炸事故的发生。
目前,已有部分学者对煤矿瓦斯爆炸事故进行了分析研究。郭慧敏等[3]对瓦斯爆炸事故致因进行分析,运用DEMATEL方法定量分析各致因之间相互影响关系,并结合ISM-MICMAC方法,探求导致事故发生的原因以及各要素的属性特征,并提出相应的对策措施;解镕嘉等[4]在基于熵权物元可拓理论的基础上结合可拓学原理,评价出煤矿瓦斯爆炸危险性等级;景国勋等[5]采用三类危险源理论、事故致因理论、层次分析法、集对分析−可变模糊集耦合方法,建立了煤矿瓦斯爆炸风险评价模型,并通过实例验证了模型的可行性;李红霞等[6]提出了一种基于LSTM的综采工作面瓦斯涌出预测及风险评估方法,对瓦斯爆炸风险等级进行了评估;汪圣伟等[7]利用事故树(FTA)、层次分析法(AHP)和集对分析法(SPA),建立了瓦斯爆炸风险评价模型,并通过实际案例验证该模型的精度;鲁锦涛等[8]分析了以往典型瓦斯爆炸案例,通过集成灰色系统理论和物元可拓模型,构建了灰色−物元评估模型,评估出瓦斯爆炸风险等级;李红霞等[9]利用模糊Bow-tie模型对煤矿瓦斯爆炸事故进行了定性和定量分析,运用风险矩阵进行了瓦斯爆炸事故风险评价;皮子坤等[10]结合前景理论与模糊综合评价理论,建立了基于区间数的煤矿瓦斯爆炸风险模糊综合评价模型,并运用模型对某地煤矿进行了风险评估,其评价结果与煤矿的生产实际情况一致;张津嘉等[11]构建了瓦斯爆炸事故风险耦合层次网络模型,并利用N-K模型分析了风险因素之间的耦合关系。
由于煤矿瓦斯爆炸是动态变化的过程,上述研究局限于静态控制管理,同时缺乏对不确定性的推理。作为不确定性推理和数据分析的工具,贝叶斯网络(BN)被广泛用于实现不确定性知识的表示和推理[12-13]。目前,已有部分学者利用贝叶斯网络对煤矿事故进行分析研究。李金蓉等[14]为了评估煤矿通风系统风险,引入DS理论−贝叶斯网络模型,以实际调研数据为例进行风险推理和敏感性分析,得到其通风系统风险等级和敏感指标;袁奇等[15]为了全面评估地下工程火灾的风险,提出了一种基于能量和屏障理论、预先危险性分析、领结图和模糊贝叶斯网络的地下工程火灾风险评估方法;洪伟斌等[16]基于DEMATEL-ISM-BN模型,结合煤矿透水事故真实案例样本数据构建了BN模型,得出了诱发透水事故的直接因素;成连华等[17]利用扎根理论对瓦斯爆炸事故案例进行编码,通过解释结构模型建立贝叶斯网络结构,引入云模型计算贝叶斯网络节点的先验概率和条件概率,对煤矿瓦斯爆炸可能性进行评价,其结果与实际情况相符;李敏等[18]基于贝叶斯网络及模糊集理论,根据专家经验确定影响瓦斯爆炸的主要风险因素,利用三角模糊数评估风险因素的先验和条件概率,最后基于贝叶斯重要度分析完成敏感性分析,找出影响瓦斯爆炸关键风险因素。
综上,通过风险识别提取诱发煤矿瓦斯爆炸事故的关键因素,通过BN参数学习为预防煤矿瓦斯爆炸事故提供参考,提出了一种基于熵权法改进模糊贝叶斯网络瓦斯爆炸危险性评估方法。
1. 评估模型概述
故障树分析[19](FTA)用于确定顶事件的潜在原因,在故障树中事件之间的关系通过门来表示,建立完成后,可以进行定性和定量分析,是一种非常流行和普及的技术,用于大型安全关键系统的可靠性建模和评估。
1.1 模糊贝叶斯网络模型概述
1.1.1 模糊理论
模糊理论[20](FST)可以表达人类判断的模糊性、模糊性和主观性。采用三角模糊数来表示事件的发生概率。隶属度函数${\mu }({x}) $计算如下;
$$ {\mu }({x})=\left\{\begin{array}{ll}0& x<a\\ \dfrac{{x}-{a}}{{r}-{a}}& a\leqslant x\leqslant r\\ \dfrac{{b}-{x}}{{b}-{r}}& r\leqslant x\leqslant b\\ 0& x>b\end{array}\right. $$ (1) 式中:a、r、b分别为最小可能值、最可能的值、最大可能值。
三角模糊数m1=(a1,r1,b1)、m2=(a2,r2,b2)有如下运算法则:
$$ \left\{\begin{array}{c}{{m}}_{1}\oplus {{m}}_{2}=({{a}}_{1}+{{a}}_{2},{{r}}_{1}+{{r}}_{2},{{b}}_{1}+{{b}}_{2})\\ {{m}}_{1}\ominus {{m}}_{2}=({{a}}_{1}-{{a}}_{2},{{r}}_{1}-{{r}}_{2},{{b}}_{1}-{{b}}_{2})\\ {{m}}_{1}\otimes {m}_{2}=({{a}}_{1}{{a}}_{2},{{r}}_{1}r,{{b}}_{1}{{b}}_{2})\\ {{m}}_{1}\oslash {m}_{2}=({{a}}_{1}/{{a}}_{2},{{r}}_{1}/{{r}}_{2},{{b}}_{1}/{{b}}_{2})\end{array}\right. $$ (2) 1.1.2 贝叶斯网络模型
通过结合领域知识和实际观测数据,贝叶斯网络可以提供更准确的概率推断结果[21]。贝叶斯网络是1个概率图模型[16],由2个重要部分组成,分别是贝叶斯网络拓扑图和节点之间的条件概率表。贝叶斯理论的主要计算公式如下:
$$ {P}\left({Y}|{X}\right){P}\left({X}\right)={P}({X}\cap {Y} ) $$ (3) $$ {P}\left({X}|{Y}\right)={P}\left({Y}|{X}\right){P}\left({X}\right){P}\left({Y}\right) $$ (4) 式中:P(Y|X)为事件X已经发生的条件下事件Y发生的概率;P(X)为事件X的先验概率;P(X|Y)为事件Y已经发生的条件下事件X发生的概率。
$$ {P}\left({Y}\right)=\sum _{{i}=1}^{{n}}{P}\left({{X}}_{{i}}\right){P}\left({Y}\right|{{X}}_{{i}}) $$ (5) $$ {P}\left({{X}}_{1},{{X}}_{2},\cdots, {{X}}_{{n}}\right)=\prod _{{i}=1}^{{n}}{P}\left({{X}}_{{i}}|{\pi }\left({{X}}_{{i}}\right)\right) $$ (6) 式中:P(Xi)为Xi的根节点集合;$ P({X}_{1},{X}_{2},\cdots , {X}_{n}) $为Xi中间节点的条件概率分布。
1.1.3 故障树与贝叶斯的映射
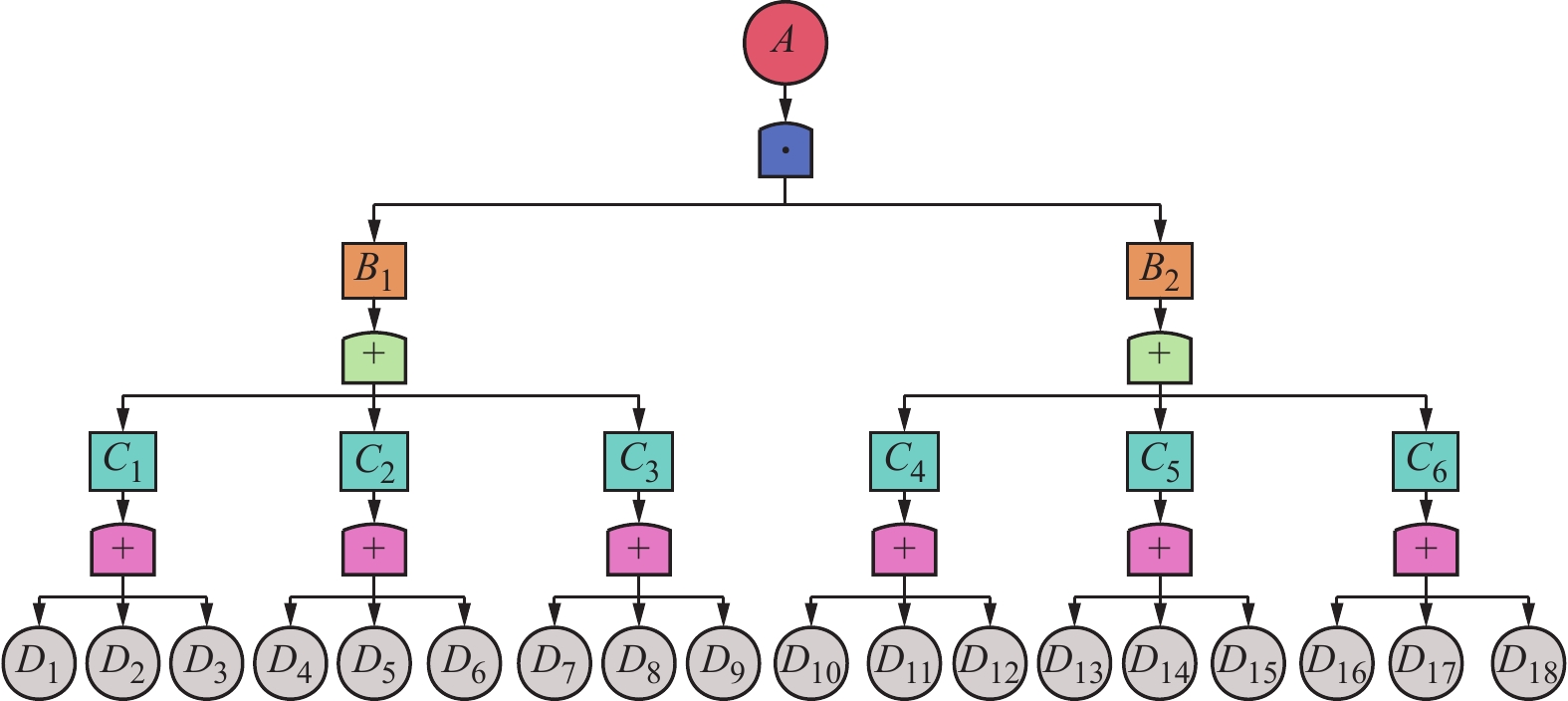
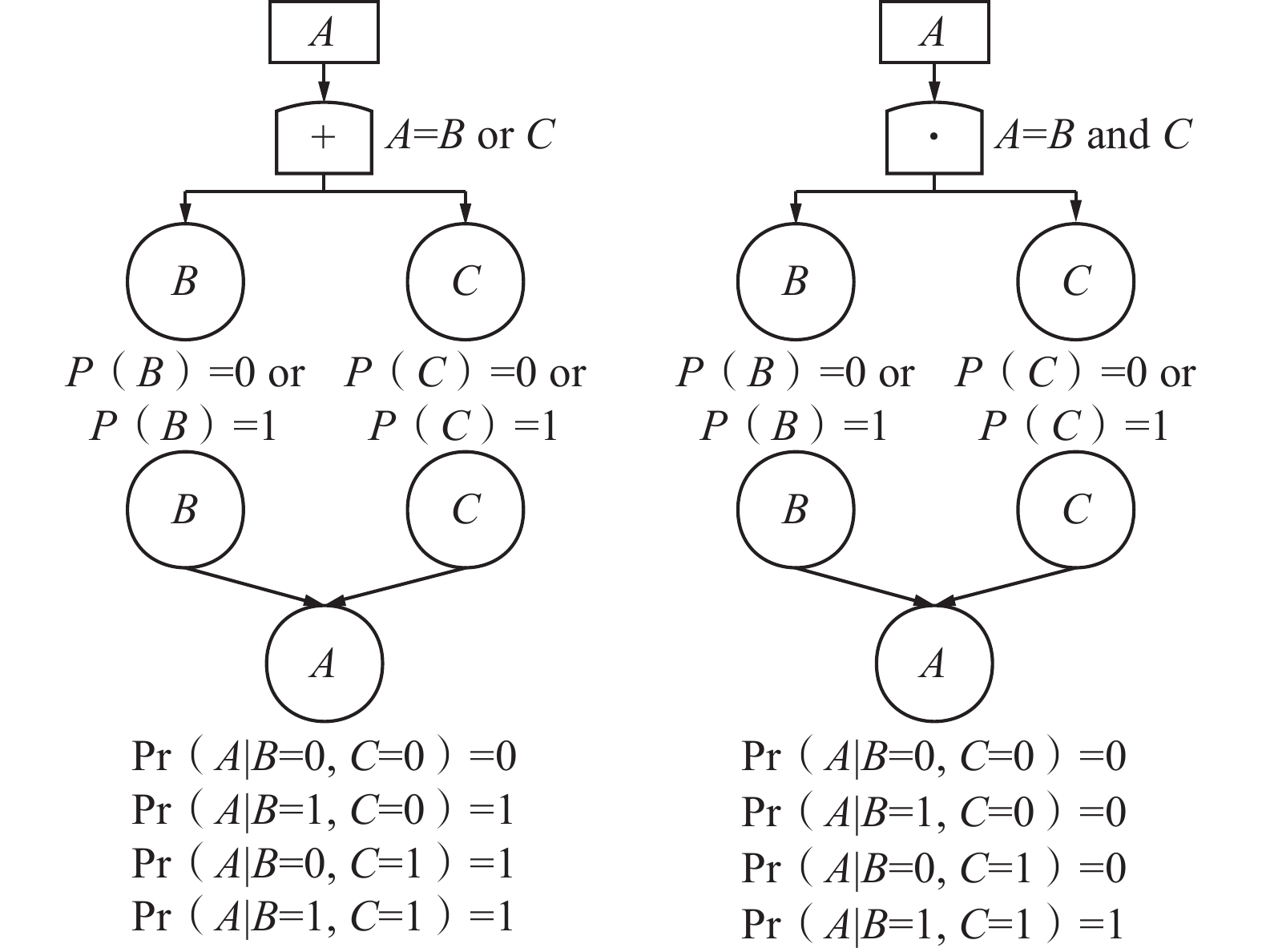
贝叶斯网络相比于传统故障树等可靠度模型,具有更加直观、清晰、更好的建模与分析功能[13]。但贝叶斯网络难以直接用于复杂系统的建模,然而基于故障树的贝叶斯网络模型可以有效地减少该问题的求解。因此,首先构建煤矿瓦斯爆炸的故障树模型,然后将其映射到瓦斯爆炸贝叶斯网络中。故障树和贝叶斯的映射如图1所示,图1中:Pr为概率值。
1.2 模糊综合评价
由于煤矿瓦斯爆炸因素受环境变化影响很大,很难用确定的数学公式进行量化表示。因此,将模糊理论引入到煤矿瓦斯爆炸贝叶斯网络中[13]。由于专家专业领域不同,因此提出以专家主观信度来衡量专家的判断信度。模糊概率区间的划分见表1,专家组的权重标准见表2。
表 1 模糊概率区间的划分Table 1. Division of fuzzy probability interval评语等级 三角模糊函数 评语等级 S1 (0.0,0.0,0.1) 非常低 S2 (0.0,0.1,0.3) 低 S3 (0.1,0.3,0.5) 较低 S4 (0.3,0.5,0.7) 中等 S5 (0.5,0.7,0.9) 较高 S6 (0.7,0.9,1.0) 高 S7 (0.9,1.0,1.0) 非常高 表 2 专家组的权重标准Table 2. Weight standard of expert group属性 描述 权重 专家职位 高级工程师 1.0 中级工程师 0.8 初级工程师 0.6 技术人员 0.4 工人 0.2 教育程度 博士 1.0 硕士 0.8 学士 0.6 大专 0.4 中专 0.2 工作年限 ≥20 年 1.0 15~<20 年 0.8 10~<15年 0.6 5~<10 年 0.4 <5 年 0.2 专业相关 非常相关 1.0 比较相关 0.8 一般相关 0.6 基本相关 0.4 不太相关 0.2 根据式(7)、式(8)可以将多位专家对底事件索引节点Xi的评价意见转化为三角模糊数。
$$ {P}_{i}^{k}=({A}_{i}^{k},{B}_{i}^{k},{C}_{i}^{k}) $$ (7) $$ {P}_{ij}^{k}={P}_{i}^{k} {\omega }_{j}=({A}_{ij}^{k},{B}_{ij}^{k},{C}_{ij}^{k}) $$ (8) 式中:$ {P}_{i}^{k} $为根节点发生的概率;$ {A}_{i}^{k}\mathrm{、}{B}_{i}^{k}\mathrm{、}{C}_{i}^{k} $分别为三角模糊数;i为根节点数;j为根节点判断状态;k为专家人数;ωj为专家综合主客观权重。
将每位专家给出的评价结果根据式(9)进行平均化处理,得到模糊均值概率。然后根据式(10)采用面积均值法将模糊均值概率转化成代表此模糊集合的概率值:
$$ P_{ij}^*=\frac{P_{ij}^1+\cdots+P_{ij}^n+\cdots P_{ij}^m}{k}=(A_{ij}^*,B_{ij}^*,C_{ij}^*) $$ (9) $$ {P}_{ij}^{**}=\frac{{A}_{ij}^{*}+{2B}_{ij}^{*}+{C}_{ij}^{*}}{4} $$ (10) 式中:$ A_{ij}^*、B_{ij}^*、C_{ij}^* $分别为平均化处理后的三角模糊数;$ {P}_{ij}^{*} $为模糊均值概率值;$ {P}_{ij}^{**} $为模糊集合的概率值。
1.3 基于熵权法修正指标权重
熵权法可用来度量不确定性系统的特征[22]。利用信息熵来修正指标的差异大小,可以得到有效的评价结果,步骤如下:
1)建立矩阵。通过收集原始数据,得到指标矩阵A。
$$ \boldsymbol{A}=\boldsymbol{A}\left(P_{ij}\right)mn $$ (11) 式中:A$ \left({P}_{ij}\right) $为评价矩阵;m为评价指标;n为评价方案。
2)指标标准化。在评价指标时一些指标的计量度并不一致,应把它们的绝对值转化为相对值。
$$ {X}_{ij}'=\frac{{X}_{ij}-{\mathrm{min}}\left\{{X}_{1j},\cdots ,{X}_{nj}\right\}}{{\mathrm{max}}\left\{{X}_{1j},\cdots, {X}_{nj}\right\}-{\mathrm{min}}\left\{{X}_{1j},\cdots, {X}_{nj}\right\}} $$ (12) $$ {X}_{ij}''=\frac{{\mathrm{max}}\left\{{X}_{1j},\cdots ,{X}_{nj}\right\}-{X}_{ij}}{{\mathrm{max}}\left\{{X}_{1j},\cdots, {X}_{nj}\right\}-{\mathrm{min}}\left\{{X}_{1j},\cdots, {X}_{nj}\right\}} $$ (13) 式中:$ {X}_{ij}' $为正向指标,其数值越大越好;$ {X}_{ij}'' $为负向指标,其数值越小越好。
3)计算第j项指标下的第i个取样值与指数的比例$ {P}_{ij} $。
$$ {P}_{ij}=\frac{{X}_{ij}}{\displaystyle\sum _{i=1}^{n}{x}_{ij}} $$ (14) 4)计算第j项指标熵值${E}_{j} $。
$$ {E}_{j}=-k\sum _{i=1}^{n}{P}_{ij} \mathrm{ln}{(P}_{ij}) $$ (15) 式中:$ k=1/\mathrm{ln}\;m $。
5)计算信息熵冗余度${D}_{j} $。
$$ {D}_{j}=1-{E}_{j} $$ (16) 6)计算各项指标的权重${W}_{j} $。
$$ {W}_{j}=\frac{{D}_{j}}{\displaystyle\sum _{j=1}^{m}{D}_{j}} $$ (17) 7)计算各样本的综合得分${S}_{i} $。
$$ {S}_{i}=\sum _{j=1}^{m}{W}_{j}{X}_{ij} $$ (18) 8)综合权重U。
$$ U=\sum _{i=1}^{m}{S}_{i}{W}_{j} $$ (19) 2. 案例研究
2.1 煤矿瓦斯爆炸风险评估
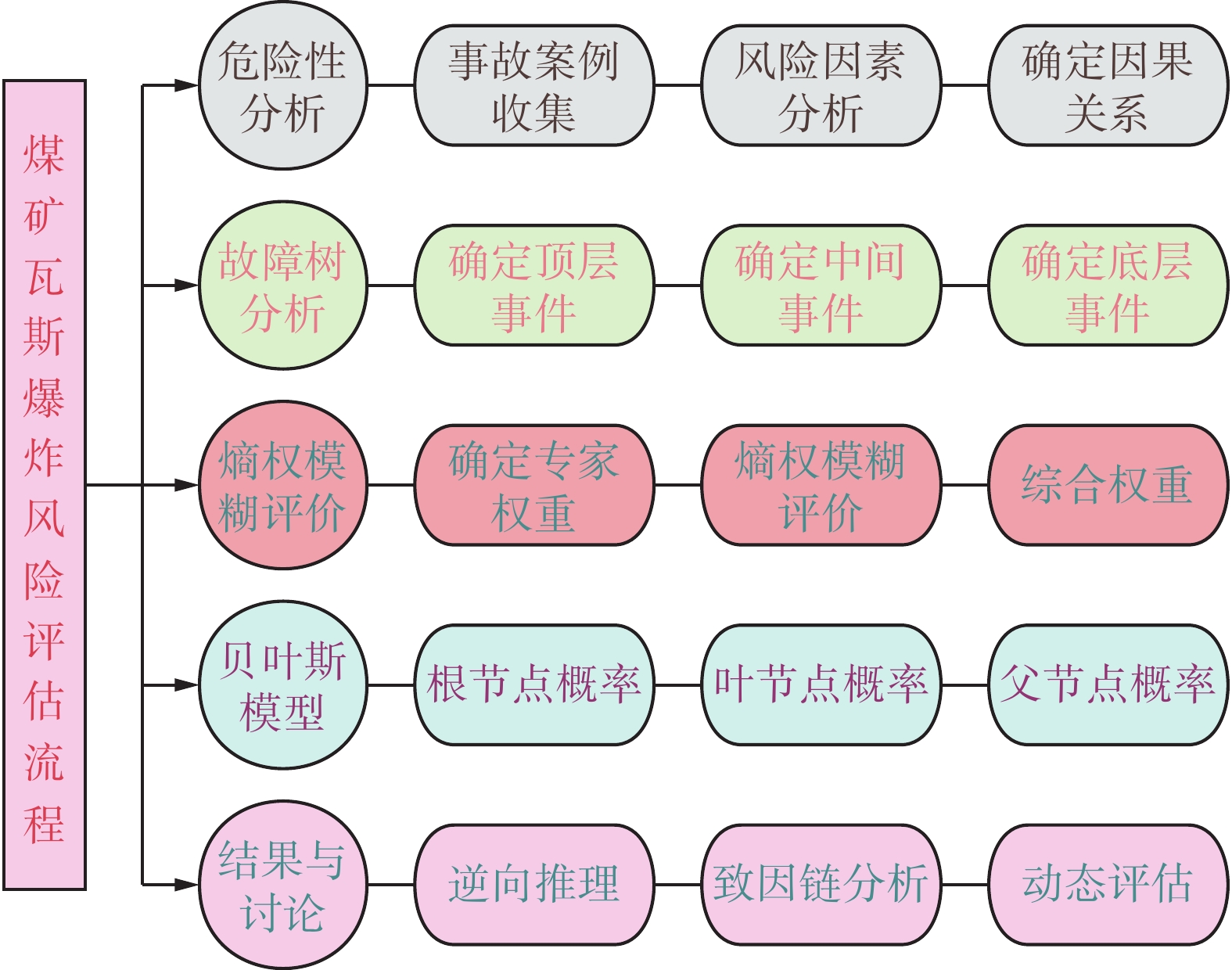
基于文献[18]和相关瓦斯爆炸事故的案例以及事故调查报告等,进行分析总结。其中,提出的18个主要因素是根据瓦斯爆炸风险因素的2个前提条件:点火源和可燃物(由于井下需要进行通风,所以没有考虑将氧气作为风险因素),并构建出煤矿瓦斯爆炸的FTA模型,其次通过映射转换为BN模型,最后结合熵权法与模糊理论,组合赋权得出各指标的概率,评估得出煤矿瓦斯爆炸的风险。煤矿瓦斯爆炸风险评估流程图如图2所示,煤矿瓦斯爆炸因素见表3。
表 3 煤矿瓦斯爆炸因素Table 3. Coal mine gas explosion factors叶节点 根节点 事件描述 瓦斯措施C1 钻孔数量D1 钻孔的数量不够 密封质量D2 封孔质量差,导致密闭性不够 瓦斯抽采D3 没有进行瓦斯抽采;瓦斯抽采不达标 通风缺陷C2 通风不足D4 风量不足,不能满足矿井通风要求 通风阻力D5 巷道变形、巷道设计缺陷等 风机故障D6 没有通风设备;风机停止运行 浓度上升C3 瓦斯积聚D7 上隅角、盲巷、采空区出现瓦斯积聚 瓦斯涌出D8 瓦斯涌出量异常 瓦斯突出D9 瞬间释放大量瓦斯和煤 产生火花C4 摩擦火花D10 岩石,设备等摩擦产生火花 撞击火花D11 物体碰撞产生撞击火花 静电火花D12 物体接触产生静电火花 电气故障C5 电器故障D13 电气设备短路及故障等产生火花 防爆故障D14 防爆设备失效或没有防爆设备 设施故障D15 电缆老化、断裂产生火花 出现明火C6 违规爆破D16 爆破作业没有按照规范制度进行 煤炭自燃D17 煤体升温到着火点,与氧气反应燃烧 使用明火D18 人员吸烟,明火照明,焊接等 2.2 实例验证
煤矿位于贵州盘州市松河乡,设计生产能力30万t/a,属于煤与瓦斯突出矿井。矿井采用斜井、平硐联合开拓,并列抽出式通风,矿井主井进风
2252 m3/min,副井进风893 m3/min,总回风量为3465 m3/min。通过对煤矿瓦斯爆炸主要因素进行分析后,构建出松林煤矿瓦斯爆炸的FTA模型,煤矿瓦斯爆炸的FTA模型如图3所示。2.3 综合评价
在矿山生产过程中,由于氧浓度条件易于满足[23]。因此,只考虑瓦斯超限(B1)和点火源(B2)2个主要因素。若风险换成其他因素,则概率会有所不同,但通过模糊理论和熵权法对数据进行处理后,得出的结果可以降低主观性,提高评价的客观性。因此,邀请了对该领域的专家对所有节点的概率进行判断,专家信息见表4,专家打分情况见表5,节点的概率见表6。
表 4 专家信息Table 4. Expert information序号 专家职位 工作年限/年 学历 专业相关 1 高级工程师 22 博士 非常相关 2 中级工程师 18 硕士 比较相关 3 初级工程师 12 本科 比较相关 4 技术人员 8 硕士 非常相关 表 5 专家打分表Table 5. Expert scoring table指标 专家 权重
均分信息熵 模糊
权重综合
权重1 2 3 4 D1 8 8 7 8 6.037 5 0.7809 0.2185 0.1706 D2 7 6 6 7 5.062 5 0.7044 0.1743 0.1228 D3 6 5 5 4 3.962 5 0.5980 0.6072 0.3631 D4 7 7 6 6 5.100 0 0.7076 0.2958 0.2093 D5 6 6 5 6 4.487 5 0.6520 0.3386 0.2208 D6 8 7 7 7 5.675 0 0.7540 0.3656 0.2757 D7 7 6 6 7 5.062 5 0.7044 0.3711 0.2614 D8 6 5 4 5 3.962 5 0.5980 0.2347 0.1404 D9 6 5 5 5 4.125 0 0.6154 0.3942 0.2426 D10 4 4 3 3 2.775 0 0.4433 0.3172 0.1406 D11 4 3 3 4 2.737 5 0.4374 0.4655 0.2036 D12 3 2 3 2 1.962 5 0.2928 0.2173 0.0636 D13 6 6 5 5 4.325 0 0.6360 0.2914 0.1853 D14 7 6 7 7 5.225 0 0.7181 0.3833 0.2752 D15 6 5 6 7 4.612 5 0.6639 0.3253 0.2160 D16 9 8 7 8 6.287 5 0.7985 0.4483 0.3580 D17 7 8 8 8 5.950 0 0.7745 0.4541 0.3517 D18 7 6 7 7 5.225 0 0.7181 0.0976 0.0701 表 6 节点的概率Table 6. Probability of nodes指标 概率 指标 概率 指标 概率 D1 0.171 D7 0.261 D13 0.185 D2 0.123 D8 0.140 D14 0.275 D3 0.363 D9 0.243 D15 0.216 D4 0.209 D10 0.141 D16 0.358 D5 0.221 D11 0.204 D17 0.352 D6 0.276 D12 0.065 D18 0.070 A 0.252 C1 0.190 C4 0.157 B1 0.215 C2 0.229 C5 0.251 B2 0.287 C3 0.216 C6 0.326 3. 结果与讨论
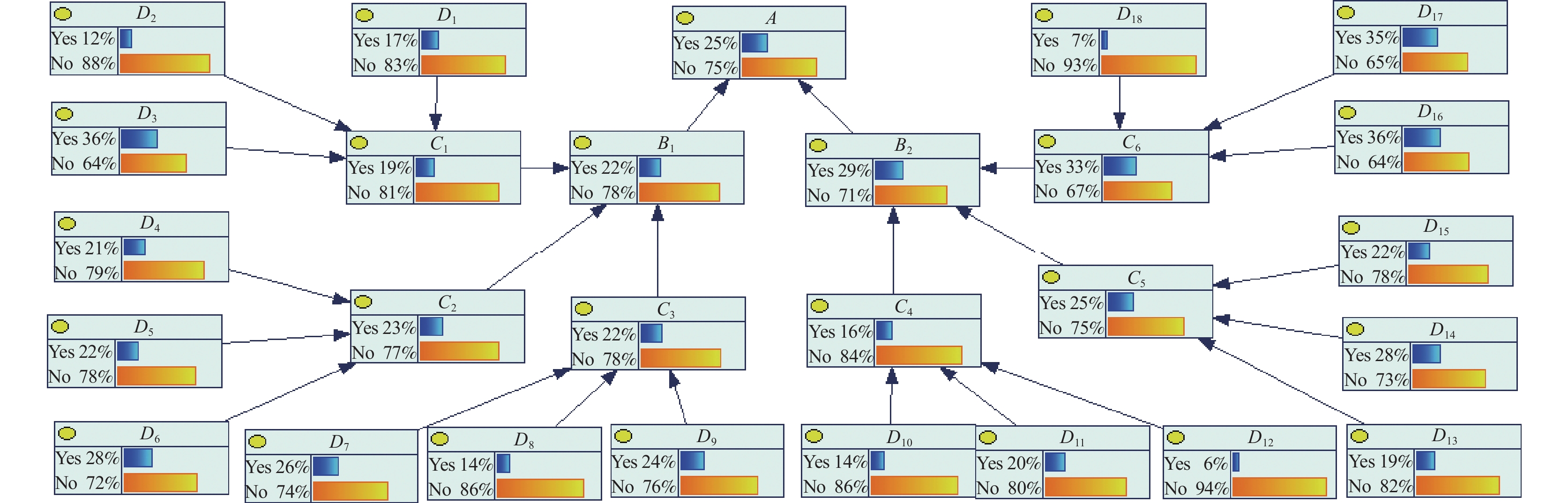
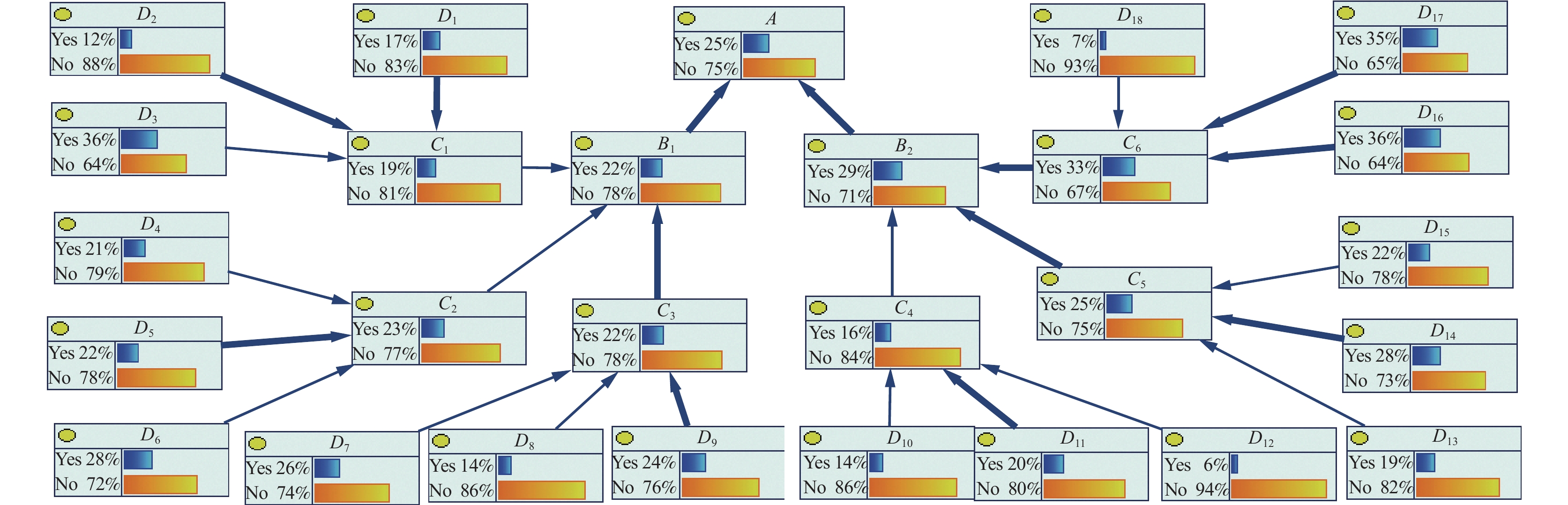
将各指标参数导入GENIE软件中,煤矿瓦斯爆炸贝叶斯网络如图4所示。
由图4分析评估可以得出,瓦斯爆炸的风险概率为25%。瓦斯爆炸风险评价结果等级为一般风险。在煤矿瓦斯爆炸基本事件中,瓦斯抽采不足的风险最高,发生的概率为36.3%;其次是煤炭自燃的风险,发生概率为35.8%。
具体来看:①在瓦斯控制措施方面,说明该矿的瓦斯抽采不达标,因此需要加强瓦斯抽采,降低瓦斯含量。在通风故障方面,风机故障发生概率为27.6%,通风阻力发生概率为22.1%,风量不足发生概率为20.9%,主要是该矿风机设备出现过几次停机的现象,而且在风机运行过程中,由于风机阻力较大,因此导致通风量不足;②在瓦斯浓度上升方面,瓦斯积聚的概率为26.1%,瓦斯突出的概率为24.3%,瓦斯涌出异常的概率为14%,通过检测装置发现,在上隅角、盲巷及采空区等都有一定量的瓦斯积聚,且该矿属于突出矿井;③在产生电火花方面,摩擦火花发生概率为14.1%,撞击火花发生概率为20.4%,静电火花发生概率为6.4%,主要是因为在生产过程中,设备之间存在着摩擦,岩石发生碰撞都会产生火花;④在电气故障方面,电器设施故障发生概率为18.5%,电器设备故障发生概率为27.5%,防爆设备发生故障概率为21.6%,由于电线的老化和设备超负荷运转,出现线缆断裂和设备短路等,以及防爆设备老化长期没有进行维护;⑤在出现明火方面,煤自燃发生的概率为35.8%,违规爆破发生的概率为35.8%,使用明火发生的概率为7%。说明该煤层有一定的自燃倾向性,由于煤易与空气接触发生氧化,使煤的温度升高,同时又使煤的燃点降低,因此容易引起煤的自燃,此外,由于地质构造变动或因采掘而破碎,以及通风不良等,也是引起自燃的因素;⑥在违规爆破方面,说明管理人员的监管没有到位,技术人员的安全意识薄弱等,因此需要重点加强对煤自燃的控制和规范爆破流程,同时要加强监管力度,开展安全教育培训,提高管理者的管理水平和人员的安全防范意识。
3.1 逆向推理和致因链分析
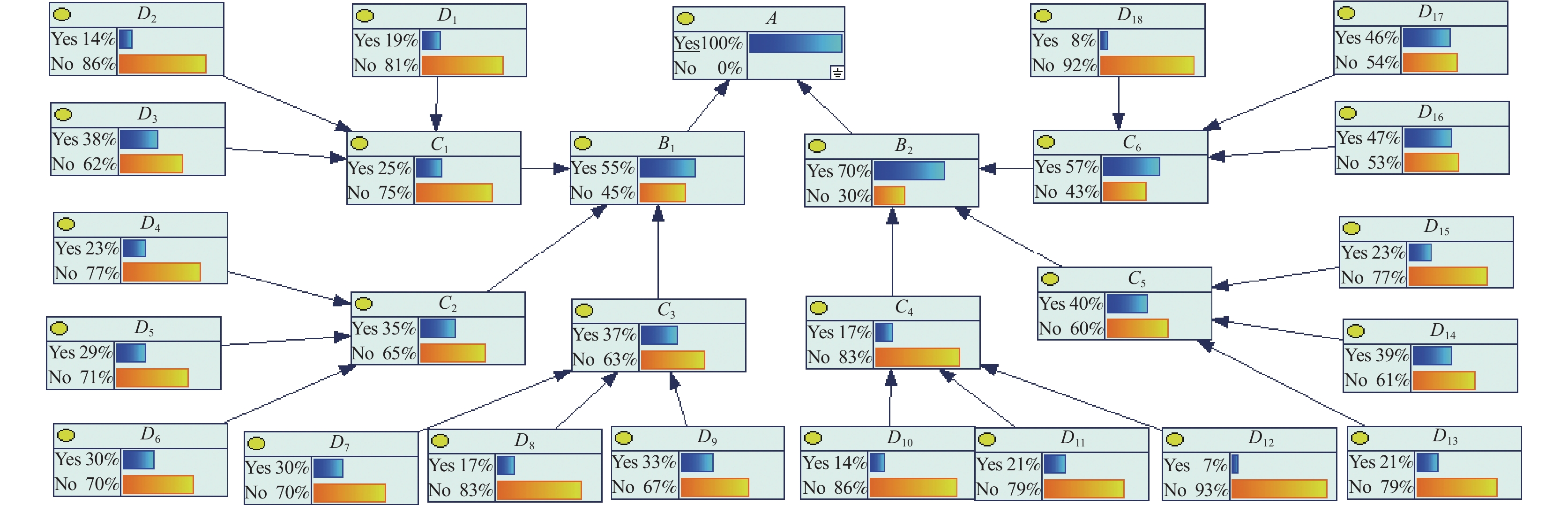
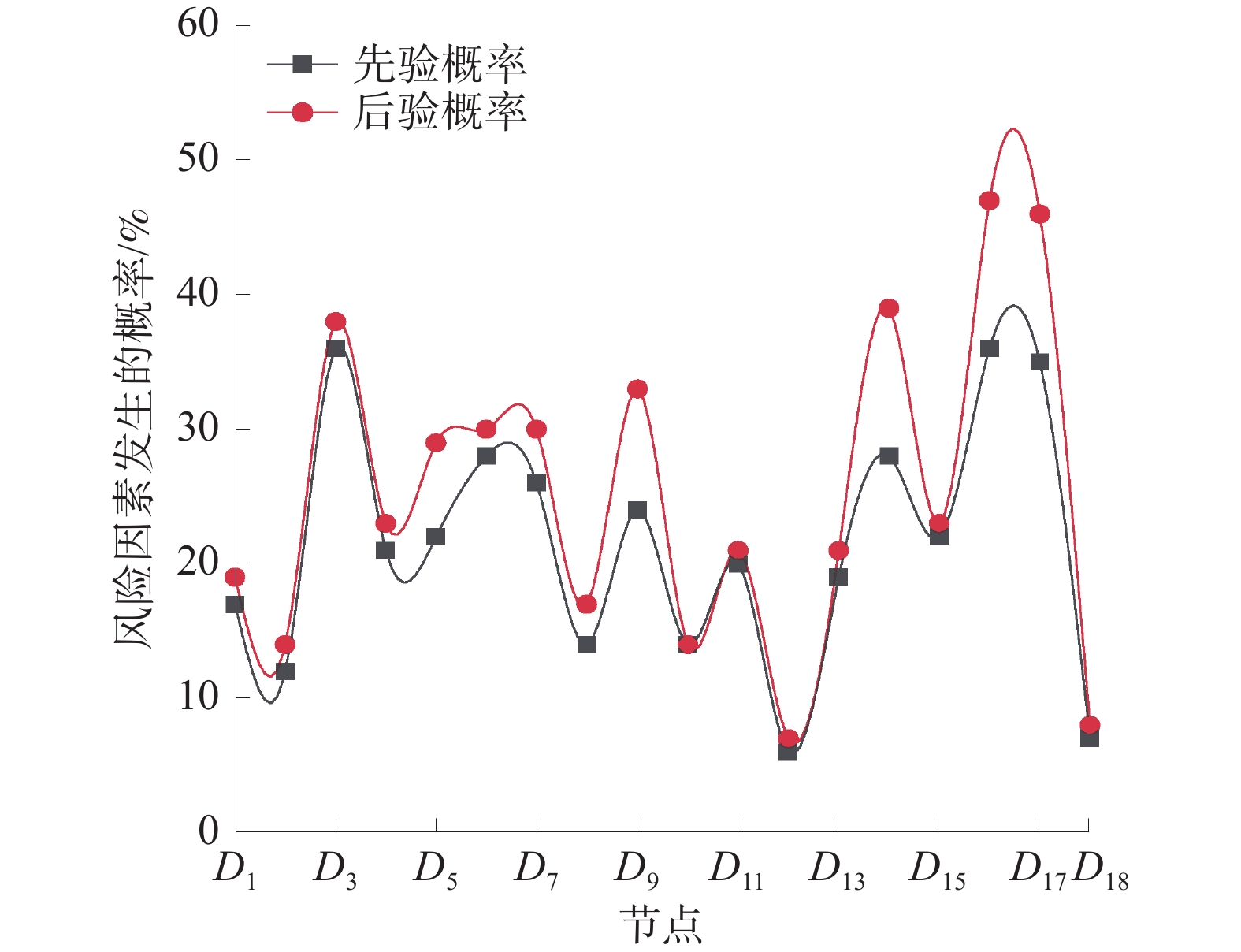
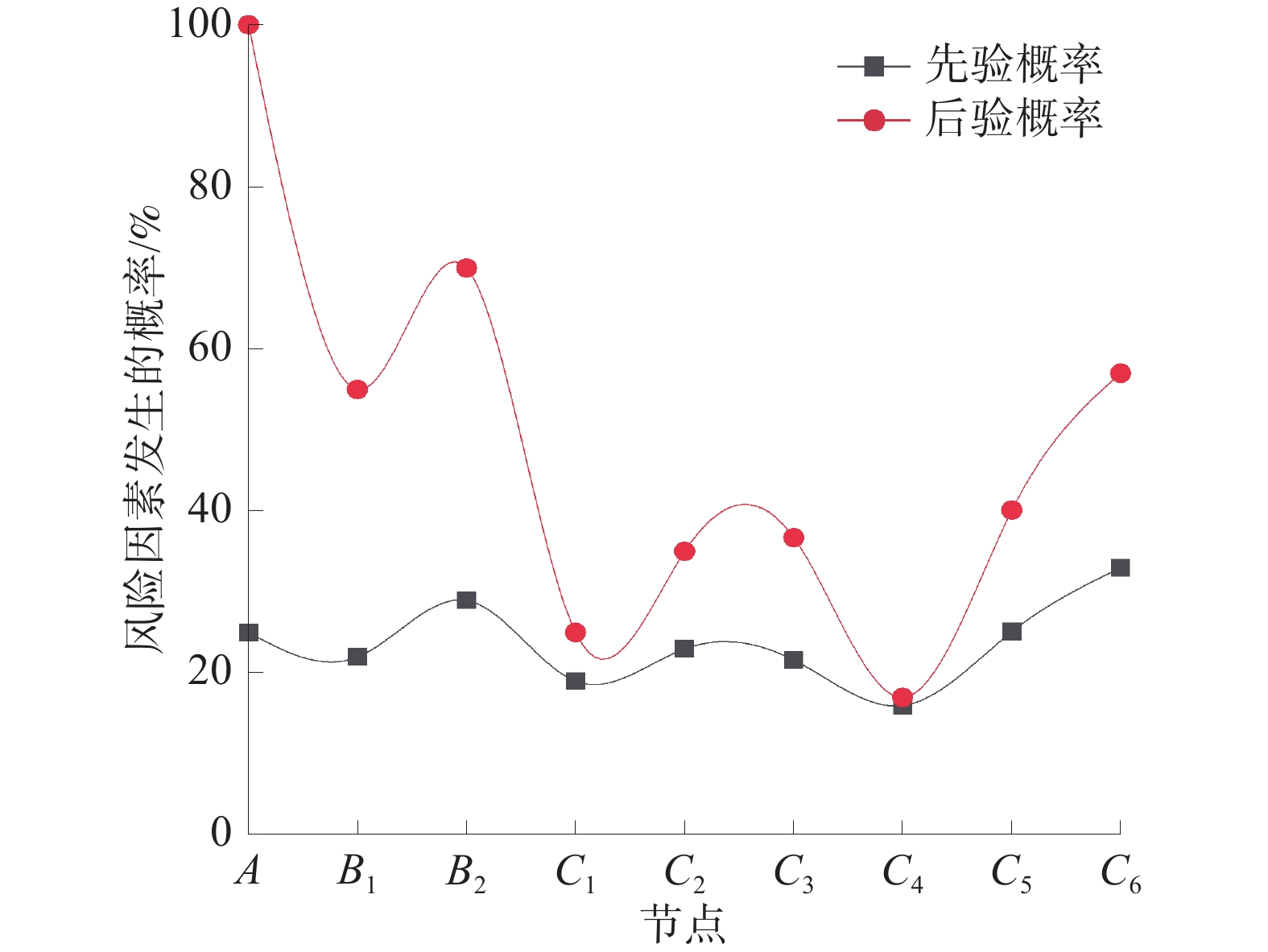
在数据相当有限的情况下,可以利用逆向推理和致因链分析分别对煤矿瓦斯爆炸的安全状况做初步判断。在GENIE软件中,将顶上事件A发生的概率设置为1,从而进行逆向推理。贝叶斯网络的逆向推理图如图5所示,三级指标概率变化如图6所示,一级和二级指标概率变化如图7所示,贝叶斯网络的致因链如图8所示。图8中箭头越粗代表着上一级因素对下一级因素的致因影响就越大。
1)一级指标。瓦斯超限(B1)的概率从22%增加到55%,增加了33%;点火源(B2)的概率,从29%增加到70%,增加了41%;变化大小排序为:B2>B1。
2)二级指标。瓦斯控制(C1)的概率从19%增加到25%,增加了6%;通风缺陷(C2)的概率从23%增加到35%,增加了12%;瓦斯浓度上升(C3)的概率从21.57%增加到36.69%,增加了15.12%;电火花(C4)的概率从16%增加到17%,增加了1%;电气故障(C5)的概率从25.11%增加到40.05%,增加了14.94%;出现明火(C6)的概率从33%增加到57%,增加了24%;变化大小排序为:C6>C3>C5>C2>C1>C4,其中出现明火、瓦斯浓度上升、电气故障及通风缺陷4个指标均增加了12%及以上。
3)三级指标。三级指标变化较大的包括:通风阻力、瓦斯突出、防爆设备故障、违规爆破、煤炭自燃,这5个指标均增加了7%及以上。
由图8通过可以得出:通风阻力对通风故障的影响较大;瓦斯突出对瓦斯浓度上升的影响较大;撞击火花更容易产生电火花;电气故障中的防爆设备故障发生的风险更大;违规爆破和煤炭自燃更可能导致明火出现。因此,应加强对风机进行检修和维护,以保证足量的风量。加大对煤层瓦斯的抽采,减少瓦斯突出的风险。及时更换防爆设备,防止设备起火。规范爆破规章制度,严格审批流程,加大监管力度。注重煤炭自燃的防治,减少煤自燃发生的风险。
综上分析,防止煤矿瓦斯爆炸需要减少通风阻力,加强通风,维护通风设备;加强瓦斯抽采,防止瓦斯突出;及时更换防爆设备,加强监管力度和严格规范爆破流程,重点对煤自燃的防治加大技术研究投入。
3.2 动态评估
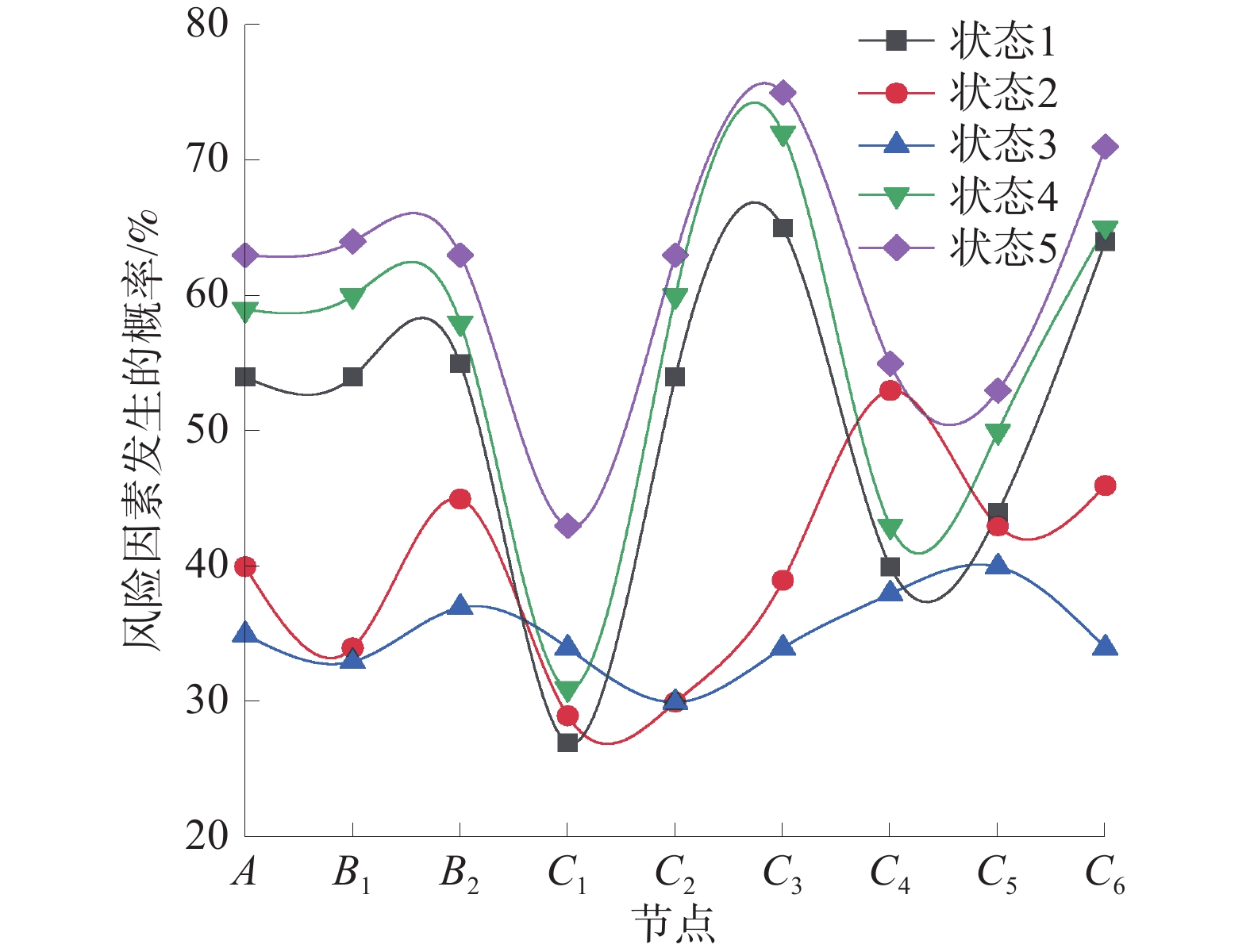
由于煤矿内部环境是动态变化的,因此有必要对其因素进行动态评估,实现对煤矿的动态管理,从而更好地预防煤矿瓦斯爆炸风险。将5种状态的根节点先验概率导入到软件中,分别计算得出瓦斯爆炸风险和中间节点的风险概率。一级和二级指标不同状态的概率变化如图9所示。
由图9可以明显看出:随着矿井内部因素状态的变化,瓦斯爆炸的风险也随之发生变化;状态1的瓦斯爆炸发生风险为54 %,状态2的瓦斯爆炸发生风险为40%,状态3的斯爆炸发生风险为35%,状态4的瓦斯爆炸发生风险为59%,状态5的瓦斯爆炸发生风险为63%;状态1、状态4、状态5的瓦斯爆炸风险较高,其中状态5的风险因素概率值;状态2、状态3的瓦斯爆炸风险较低,其中状态3的瓦斯爆炸风险最低。瓦斯爆炸风险概率大小排序为状态5>状态4>状态1>状态2>状态3。
从图9还可以看出,状态5的瓦斯浓度上升的概率是最大的,需要对煤层瓦斯进行增透处理,提高瓦斯抽采效率,减少煤层瓦斯压力,以防止瓦斯积聚和瓦斯涌出异常,降低煤与瓦斯突出事故发生的风险;其次为出现明火的风险概率,需要对违规爆破进行规范化管理,提高防治煤自燃的技术手段,同时加强人员监督管理,降低点火源发生的风险;虽然最低的风险因素为瓦斯控制,但不能忽略对瓦斯控制的治理。对状态2而言,其产生电火花这个因素较高,需注意对矿井火花的抑制,减少产生火花的风险。
综上所述,煤矿应采用合理的开采技术和瓦斯抽放技术[24],防止瓦斯突出;实时监测瓦斯体积分数,防止瓦斯异常涌出;加强维护通风设备,防止瓦斯积聚。要把火灾管理的重点放在防止煤炭自燃上和煤尘的抑制[25],通过使用抑制剂防火、灌浆防火、风压调节防灭火等技术手段防止煤炭自燃[26]。此外,规范井下爆破和及时更换新的防爆设备,同时还要加强对企业员工的组织管理和安全教育培训,提高安全意识,减少事故发生的概率。
4. 结 语
1)探讨了煤矿瓦斯爆炸中风险评估的应用。由于在煤矿生产系统中,专家很难获得准确的信息,因此将故障树分析、模糊理论和贝叶斯网络方法相结合,从而解决煤矿瓦斯爆炸风险分析的不确定性问题。
2)构建了故障树和模糊贝叶斯网络模型,利用熵权法结合模糊理论组合赋权确定先验概率,并采用贝叶斯网络模型进行预测分析。通过利用GENIE软件,导入先验概率和条件概率,真实的计算出瓦斯爆炸发生的概率。
3)对贵州松林煤矿进行了瓦斯爆炸风险评估实例验证,论证了瓦斯爆炸发生的可能性。评估出该煤矿的瓦斯爆炸风险概率为25%;其瓦斯爆炸风险评价结果等级为一般风险。通过逆向推理、致因链分析和动态评估,对引起瓦斯爆炸的风险因素进行反复诊断,确定敏感风险因素,实现动态分析,验证了该风险评估方法的实用性。
-
表 1 模糊概率区间的划分
Table 1 Division of fuzzy probability interval
评语等级 三角模糊函数 评语等级 S1 (0.0,0.0,0.1) 非常低 S2 (0.0,0.1,0.3) 低 S3 (0.1,0.3,0.5) 较低 S4 (0.3,0.5,0.7) 中等 S5 (0.5,0.7,0.9) 较高 S6 (0.7,0.9,1.0) 高 S7 (0.9,1.0,1.0) 非常高 表 2 专家组的权重标准
Table 2 Weight standard of expert group
属性 描述 权重 专家职位 高级工程师 1.0 中级工程师 0.8 初级工程师 0.6 技术人员 0.4 工人 0.2 教育程度 博士 1.0 硕士 0.8 学士 0.6 大专 0.4 中专 0.2 工作年限 ≥20 年 1.0 15~<20 年 0.8 10~<15年 0.6 5~<10 年 0.4 <5 年 0.2 专业相关 非常相关 1.0 比较相关 0.8 一般相关 0.6 基本相关 0.4 不太相关 0.2 表 3 煤矿瓦斯爆炸因素
Table 3 Coal mine gas explosion factors
叶节点 根节点 事件描述 瓦斯措施C1 钻孔数量D1 钻孔的数量不够 密封质量D2 封孔质量差,导致密闭性不够 瓦斯抽采D3 没有进行瓦斯抽采;瓦斯抽采不达标 通风缺陷C2 通风不足D4 风量不足,不能满足矿井通风要求 通风阻力D5 巷道变形、巷道设计缺陷等 风机故障D6 没有通风设备;风机停止运行 浓度上升C3 瓦斯积聚D7 上隅角、盲巷、采空区出现瓦斯积聚 瓦斯涌出D8 瓦斯涌出量异常 瓦斯突出D9 瞬间释放大量瓦斯和煤 产生火花C4 摩擦火花D10 岩石,设备等摩擦产生火花 撞击火花D11 物体碰撞产生撞击火花 静电火花D12 物体接触产生静电火花 电气故障C5 电器故障D13 电气设备短路及故障等产生火花 防爆故障D14 防爆设备失效或没有防爆设备 设施故障D15 电缆老化、断裂产生火花 出现明火C6 违规爆破D16 爆破作业没有按照规范制度进行 煤炭自燃D17 煤体升温到着火点,与氧气反应燃烧 使用明火D18 人员吸烟,明火照明,焊接等 表 4 专家信息
Table 4 Expert information
序号 专家职位 工作年限/年 学历 专业相关 1 高级工程师 22 博士 非常相关 2 中级工程师 18 硕士 比较相关 3 初级工程师 12 本科 比较相关 4 技术人员 8 硕士 非常相关 表 5 专家打分表
Table 5 Expert scoring table
指标 专家 权重
均分信息熵 模糊
权重综合
权重1 2 3 4 D1 8 8 7 8 6.037 5 0.7809 0.2185 0.1706 D2 7 6 6 7 5.062 5 0.7044 0.1743 0.1228 D3 6 5 5 4 3.962 5 0.5980 0.6072 0.3631 D4 7 7 6 6 5.100 0 0.7076 0.2958 0.2093 D5 6 6 5 6 4.487 5 0.6520 0.3386 0.2208 D6 8 7 7 7 5.675 0 0.7540 0.3656 0.2757 D7 7 6 6 7 5.062 5 0.7044 0.3711 0.2614 D8 6 5 4 5 3.962 5 0.5980 0.2347 0.1404 D9 6 5 5 5 4.125 0 0.6154 0.3942 0.2426 D10 4 4 3 3 2.775 0 0.4433 0.3172 0.1406 D11 4 3 3 4 2.737 5 0.4374 0.4655 0.2036 D12 3 2 3 2 1.962 5 0.2928 0.2173 0.0636 D13 6 6 5 5 4.325 0 0.6360 0.2914 0.1853 D14 7 6 7 7 5.225 0 0.7181 0.3833 0.2752 D15 6 5 6 7 4.612 5 0.6639 0.3253 0.2160 D16 9 8 7 8 6.287 5 0.7985 0.4483 0.3580 D17 7 8 8 8 5.950 0 0.7745 0.4541 0.3517 D18 7 6 7 7 5.225 0 0.7181 0.0976 0.0701 表 6 节点的概率
Table 6 Probability of nodes
指标 概率 指标 概率 指标 概率 D1 0.171 D7 0.261 D13 0.185 D2 0.123 D8 0.140 D14 0.275 D3 0.363 D9 0.243 D15 0.216 D4 0.209 D10 0.141 D16 0.358 D5 0.221 D11 0.204 D17 0.352 D6 0.276 D12 0.065 D18 0.070 A 0.252 C1 0.190 C4 0.157 B1 0.215 C2 0.229 C5 0.251 B2 0.287 C3 0.216 C6 0.326 -
[1] 武强,涂坤,曾一凡,等. 打造我国主体能源(煤炭)升级版面临的主要问题与对策探讨[J]. 煤炭学报,2019,44(6):1625−1636. WU Qiang, TU Kun, ZENG Yifan, et al. Discussion on the main problems and countermeasures of building China’s main energy(coal) upgraded version[J]. Journal of China Coal Society, 2019, 44(6): 1625−1636.
[2] 赵佳佳,田世祥,杨家向,等. 基于知识图谱的煤矿热动力灾害可视化研究[J]. 煤矿安全,2023,54(3):33−39. ZHAO Jiajia, TIAN Shixiang, YANG Jiaxiang, et al. Study on visualization of thermodynamic disaster in coal mine based on knowledge map[J]. Safety in Coal Mines, 2023, 54(3): 33−39.
[3] 郭慧敏,成连华,李树刚. 基于DEMATEL-ISM-MICMAC的煤矿瓦斯爆炸致因研究[J]. 矿业安全与环保,2023,50(2):114−119. GUO Huimin, CHENG Lianhua, LI Shugang. Research on causal factors of coal mine gas explosion based on DEMATEL-ISM-MICMAC[J]. Mining Safety & Environmental Protection, 2023, 50(2): 114−119.
[4] 解镕嘉,谢雄刚,殷涛,等. 基于熵权物元可拓模型的煤矿瓦斯爆炸危险性评价[J]. 化工矿物与加工,2023,52(8):32−38. XIE Rongjia, XIE Xionggang, YIN Tao, et al. The risk evaluation of gas explosion in coal mines by matter-element extension model based on entropy weight[J]. Industrial Minerals & Processing, 2023, 52(8): 32−38.
[5] 景国勋,陈纪宏. 基于SPA-VFS耦合模型的瓦斯爆炸风险评价[J]. 安全与环境学报,2023,23(7):2151−2158. JING Guoxun, CHEN Jihong. Risk assessment of gas explosion based on SPA-VFS coupling model[J]. Journal of Safety and Environment, 2023, 23(7): 2151−2158.
[6] 李红霞,吴雪菲,谢谦. 综采工作面瓦斯爆炸风险评估[J]. 西安科技大学学报,2022,42(2):245−250. LI Hongxia, WU Xuefei, XIE Qian. Gas risk assessment of fully-mechanized mining face[J]. Journal of Xi’an University of Science and Technology, 2022, 42(2): 245−250.
[7] 汪圣伟,李希建,代芳瑞,等. 基于改进AHP-SPA的煤矿瓦斯爆炸风险评价[J]. 矿业研究与开发,2021,41(4):113−117. WANG Shengwei, LI Xijian, DAI Fangrui, et al. Risk assessment of gas explosion based on improved AHP-SPA[J]. Mining Research and Development, 2021, 41(4): 113−117.
[8] 鲁锦涛,任利成,戎丹,等. 基于灰色-物元模型的煤矿瓦斯爆炸风险评估[J]. 中国安全科学学报,2021,31(2):99−105. LU Jintao, REN Licheng, RONG Dan, et al. Assessment of coal mine gas explosion risk based on grey-matter element model[J]. China Safety Science Journal, 2021, 31(2): 99−105.
[9] 李红霞,郑佳敏. 煤矿瓦斯爆炸模糊Bow-tie模型分析[J]. 矿业安全与环保,2020,47(5):119−126. LI Hongxia, ZHENG Jiamin. Analysis of fuzzy Bow-tie model of gas explosion in coal mine[J]. Mining Safety & Environmental Protection, 2020, 47(5): 119−126.
[10] 皮子坤,贾宝山,贾廷贵,等. 基于前景理论和区间数的煤矿瓦斯爆炸风险评价[J]. 中国安全科学学报,2017,27(6):91−96. PI Zikun, JIA Baoshan, JIA Tinggui, et al. Assessment of risk of gas explosion in coal mine based on prospect theory and interval number[J]. China Safety Science Journal, 2017, 27(6): 91−96.
[11] 张津嘉,许开立,王延瞳,等. 瓦斯爆炸事故风险耦合分析[J]. 东北大学学报(自然科学版),2017,38(3):414−417. ZHANG Jinjia, XU Kaili, WANG Yantong, et al. Analysis of risk coupling of gas explosion accidents[J]. Journal of Northeastern University (Natural Science Edition), 2017, 38(3): 414−417.
[12] LI M, WANG D M, SHAN H. Risk assessment of mine ignition sources using fuzzy Bayesian network[J]. Process Safety and Environmental Protection, 2019, 125: 297−306. doi: 10.1016/j.psep.2019.03.029
[13] 史晓娟,姚兵,顾华北. 基于模糊贝叶斯网络的矿井排水系统故障诊断[J]. 工矿自动化,2022,48(9):77−83. SHI Xiaojuan, YAO Bing, GU Huabei. Fault diagnosis of mine drainage system based on fuzzy Bayesian network[J]. Industry and Mine Automation, 2022, 48(9): 77−83.
[14] 李金蓉,杨玉中. DS理论-贝叶斯网络下的煤矿通风系统风险评估[J]. 中国安全科学学报,2022,32(8):146−153. LI Jinrong, YANG Yuzhong. Risk assessment of ventilation system in coal mines based on DS theory and Bayesian network[J]. China Safety Science Journal, 2022, 32(8): 146−153.
[15] 袁奇,张晓蕾,张兴凯,等. 地下工程火灾综合定量风险评估方法[J]. 安全与环境学报,2024,24(1):42−52. YUAN Qi, ZHANG Xiaolei, ZHANG Xingkai, et al. Integrated quantitative risk assessment method for underground engineering fires[J]. Journal of Safety and Environment, 2024, 24(1): 42−52.
[16] 洪伟斌,盛武. 基于DEMATEL-ISM-BN的煤矿透水事故影响因素分析[J]. 工矿自动化,2022,48(12):116−122. HONG Weibin, SHENG Wu. Analysis of influencing factors of coal mine flooding accidents based on DEMATEL-ISM-BN[J]. Industrial and Mining Automation, 2022, 48(12): 116−122.
[17] 成连华,左敏昊. 基于扎根理论的瓦斯爆炸风险累积效应研究[J]. 中国安全生产科学技术,2021,17(10):53−59. CHENG Lianhua, ZUO Minhao. Research on cumulative effect of gas explosion risk based on grounded theory[J]. Journal of Safety Science and Technology, 2021, 17(10): 53−59.
[18] 李敏,林志军,鲁义,等. 基于模糊贝叶斯网络的煤矿瓦斯爆炸风险评估[J]. 煤炭学报,2023,48(S2):626−637. LI Min, LIN Zhijun, LU Yi, et al. Risk assessment of gas explosion coal mines based on fuzzy Bayesian network[J]. Journal of China Coal Society, 2023, 48(S2): 626−637.
[19] 陈雍君,李晓健,张丽,等. 故障树和模糊贝叶斯网络在管廊运维风险评估中的应用研究[J]. 安全与环境学报,2024,24(3):857−866. CHEN Yongjun, LI Xiaojian, ZHANG Li, et al. Research on the application of fault tree and fuzzy Bayesian network in utility tunnel operation and maintenance risk assessment[J]. Journal of Safety and Environment, 2024, 24(3): 857−866.
[20] 田文杰,徐吉辉,郝旭祥. 不确定条件下任务风险分析的贝叶斯网络方法[J]. 兵器装备工程学报,2023,44(1):152−158. TIAN Wenjie, XU Jihui, HAO Xuxiang. Bayesian network method for mission risk analysis under uncertainty[J]. Journal of Ordnance and Equipment Engineering, 2023, 44(1): 152−158.
[21] 姚成玉,陈东宁,王斌. 基于T-S故障树和贝叶斯网络的模糊可靠性评估方法[J]. 机械工程学报,2014,50(2):193−201. doi: 10.3901/JME.2014.02.193 YAO Chengyu, CHEN Dongning, WANG Bin. Fuzzy reliability assessment method based on T-S fault tree and Bayesian network[J]. Journal of Mechanical Engineering, 2014, 50(2): 193−201. doi: 10.3901/JME.2014.02.193
[22] 余磊,李波. 基于熵权的未确知测度理论的高层建筑火灾危险性评价[J]. 安全与环境工程,2017,24(1):115−120. YU Lei, LI Bo. Fire risk evaluation for high-rise buildings based on entropy weight and uncertainty measurement theory[J]. Safety and Environmental Engineering, 2017, 24(1): 115−120.
[23] 成连华,解萌玥,左敏昊,等. 基于ISM-BN的煤矿瓦斯爆炸风险评判方法及其应用[J]. 煤矿安全,2022,53(10):1−8. CHENG Lianhua, XIE Mengyue, ZUO Minhao, et al. Risk evaluation method of coal mine gas explosion based on ISM-BN and its application[J]. Safety in Coal Mines, 2022, 53(10): 1−8.
[24] 司荣军,李润之. 低浓度含氧瓦斯爆炸动力特性及防控关键技术[J]. 煤炭科学技术,2020,48(10):17−36. SI Rongjun, LI Runzhi. Dynamic characteristics of low-concentration oxygen-containing gas explosion and key technologies for prevention and control[J]. Coal Science and Technology, 2020, 48(10): 17−36.
[25] 赵佳佳,田世祥,李鹏,等. SiO2-H2O纳米流体强化煤尘润湿性的微观机理研究[J]. 化工学报,2023,74(9):3931−3945. ZHAO Jiajia, TIAN Shixiang, LI Peng, et al. Microscopic mechanism of SiO2-H2O nanofluids to enhance the wettability of coal dust[J]. CIESC Journal, 2023, 74(9): 3931−3945.
[26] 程方明,南凡,罗振敏,等. 瓦斯抑爆材料及机理研究进展与发展趋势[J]. 煤炭科学技术,2021,49(8):114−124. CHENG Fangming, NAN Fan, LUO Zhenmin, et al. Research progress and development trend of gas explosion suppression materials and mechanism[J]. Coal Science and Technology, 2021, 49(8): 114−124.



 下载:
下载: