Fracturing location optimization of floor coalbed methane wells with high water content in Hancheng Block
-
摘要:
为研究压裂位置对底板高含水的煤层气井产量的影响，以韩城区块11#煤层为研究背景，采用Petrel地质工程一体化软件，模拟顶板、顶板+煤层、煤层3种压裂位置对煤层气井的产量影响规律。结果表明：当煤储层距离高含水层1、5 m时，3种压裂方式均呈现低产气量、高产水量、见气时间晚的特征；当与含水层距离增大至10、15 m时，气井产水、产气量变化幅度较小。在高含水底板层影响下，3种压裂位置的累计产气量由大到小为：顶板>煤层+顶板>煤层，其中顶板压裂日产气峰值高，见气时间短、产水量低，受高含水层的影响较小，更适合底板高含水的煤层气井压裂改造。在韩城矿区对3种压裂位置进行了现场验证，证明了模拟结果的准确性，研究成果可以为高含水底板煤层压裂位置优选提供指导。
Abstract:In order to study the influence of fracturing location on the production of coalbed methane wells in floor with high water content, the 11# coal seam in Hancheng Block was taken as the research background, and Petrel integrated geological engineering software was used to simulate the influence law of three fracturing locations of roof, roof + coal seam and coal seam on the production of coalbed methane wells. The results show that when the coal reservoir is 1 m and 5 m away from the high aquifer, the three fracturing methods show the characteristics of low gas production, high water production and late gas occurrence time. When the distance from the aquifer increases to 10 m and 15 m, the variation range of water and gas production is small. Under the influence of floor high water content, the cumulative gas production of the three fracturing locations is from large to small: roof > coal seam + roof > coal seam; the coal seam, in which the roof fracturing has high peak daily gas, short gas emergence time and low water production, is less affected by high aquifer, and is more suitable for the fracturing reconstruction of coal bed gas wells with high water content in the floor. Three kinds of fracturing positions have been verified in Hancheng Mining Area, and the research results can provide guidance for the selection of fracturing location of floor coal seam with high water content.
-
我国煤层气资源开发潜力巨大[1-3]，2 000 m以浅煤层气地质资源量为30.05×1012 m3，其中可采资源量为12.50×1012 m3。2022年一季度[3]，全国煤层气产量为23×108 m3，同比增长约20.8%，仅占天然气国内供应的4.1%。我国煤层气低产的原因主要是煤储层普遍具有“三低一高”的特征，即低饱和度、低渗透性、低储层压力和高变质程度，开发难度大，目前仍然存在许多技术瓶颈，制约着我国煤层气的高效开发[4]。
煤层气开采主要依据“基质解吸−表面扩散−裂缝渗流”的产出机理，通过排水降压的方式进行[5-7]，排水效果对于煤层气开采具有重要影响。胡秋嘉等[8]通过建立压降扩展模型得出地层水动力条件越活跃、渗透率越低、地解比越小、束缚水饱和度越大，越不利于压降横向及纵向传播；赵馨悦等[9]认为在排采过程中，若排水量过大，会造成煤储层压力难以下降，达到临界解吸压力的区域很小，煤层气解吸量少，气相的相对渗透率低，气体采出困难；张健等[10]通过建立煤层气−水−固三相流动模型研究发现排水量越大，煤粉剥蚀效果越强，越容易堵塞孔道使产量降低。
煤储层压裂方式目前主要有顶板压裂与煤层直接压裂。顶板压裂可以在顶板与煤层界面形成较大面积的裂缝，提高了裂缝延伸范围和体积，增大导流能力，降低渗流阻力[11]。超大规模压裂在深部煤层已试验成功，产量较为可观，其煤储层结构较为完整，煤岩强度较高，直接压裂获得了可观的产量[12]。但对于浅层碎软煤层来说，直接压裂难以形成长导流缝且压后易产出煤粉堵塞孔道，导致压裂效果不佳[13]。对于底板为高含水层的气井，若压裂方式选取不当，水力裂缝易沟通高含水层而导致气井大量产水，造成气井产量较低甚至无产量。因此，裂缝通道及水文地质条件对煤层气降压开采效果影响至关重要[14-17]。
韩城区块部分煤层气井具有“高产水、低产气”的特征，这部分井次的共同特点是11#煤储层底板为高含水层，然而目前关于压裂改造沟通含水层对煤层气排采的影响研究较少。因此，以韩城区块11#煤层为研究对象，研究高含水层与煤储层不同距离下，顶板、顶板+煤层、煤层3种不同压裂位置对于气井产量的影响规律，以期提高煤储层改造效率，为煤层气高效开发提供技术指导。
1. 地质概况
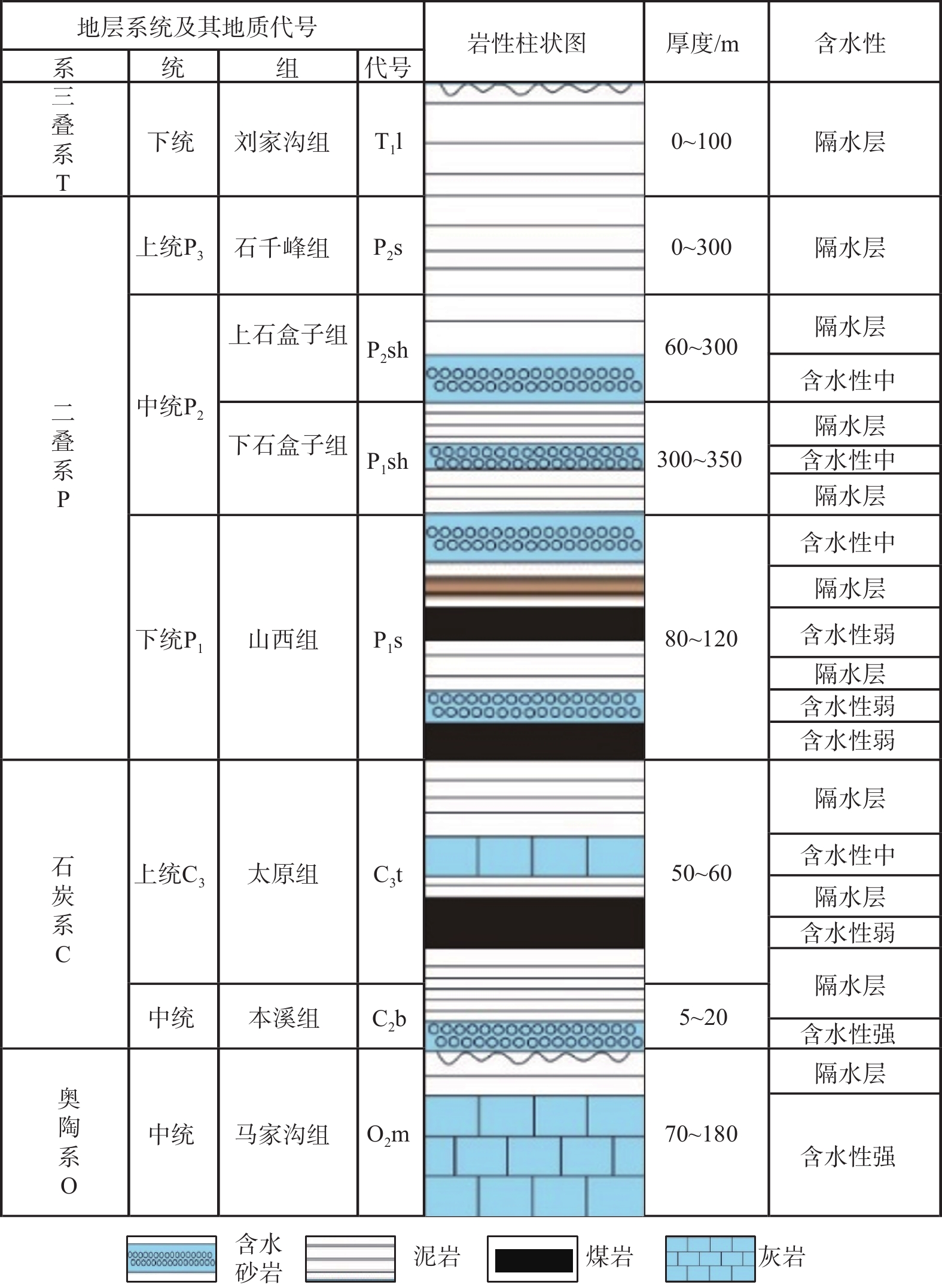
韩城区块位于鄂尔多斯盆地东南缘，渭北隆起东部断褶带北端，总体形态为北西倾的大型单斜，发育薛峰北断裂带、薛峰南断裂带和前高断裂带，整体东高西低，地层倾角1.5°~4.5°。区域构造复杂，地层沉积序列自下而上分别为下古生界奥陶系，上古生界石炭系、二叠系，中生界三叠系和新生界第四系[9]，区块内发育山西组3#、5#煤层和太原组11#煤层，其中3#煤层仅局部发育，5#煤层和11#煤层全区分布，是该区主力煤层。11#煤储层煤层气探明储量占区块整体的45.2%，但目前采出程度仅为7.6%。韩城区块水文地质情况如图1所示。
韩城区块11#煤层埋深在400~1 400 m之间，自东向西埋深逐渐变大。煤体结构破碎，以碎粒煤为主，占比59%；碎裂煤次之，占比27.82%；原生结构煤仅局部发育，占比13.18%。11#煤层属于典型的碎软煤层，煤层厚度4~6 m，煤层顶板为暗色泥岩夹条带砂，含水性中等，岩石力学参数较高，可压性较好；底板为铝土质泥岩夹杂本溪组含水砂岩，含水性强，本溪组砂岩分布不连续、厚度不稳定（一般为0~12 m），与煤层的距离为1~15 m。
2. 数值模拟
非常规缝网模型[15-16]（UFM）对于复杂裂缝地层具有较强的适用性，可以很好地耦合岩石变形与裂缝流体流动问题，对于割理裂隙发育的煤储层较为适合。在UFM模型中，采用边界元法计算固体岩石变形和应力场，采用泊肃叶定律表征缝内流体切向流动，依据断裂力学理论控制裂缝的起裂与扩展，将裂缝扩展模型进行产能网格划分，调用产能模拟器可对压后产量模拟计算，评估煤储层与高含水层不同距离下压裂位置对碎软煤层气井的产气产水影响规律。
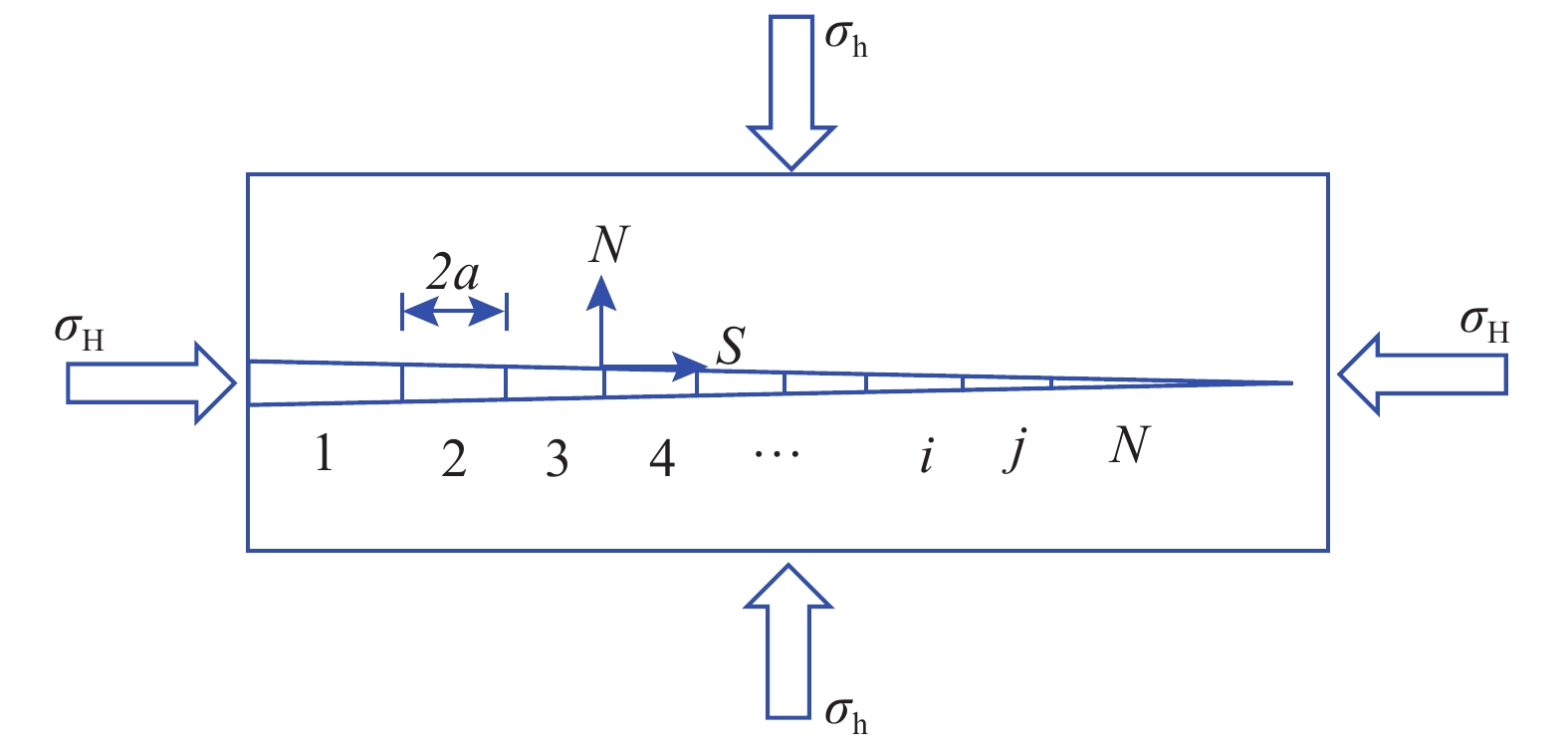
将地层中的1条复杂水力裂缝投影至平面并分成N个单元，用直线段近似表示每个裂缝单元，单元间距为a，平面面积为S。裂缝单元离散化情况如图2所示。
假设每个裂缝单元上的位移不连续量均匀分布，依据叠加原理，在单元i处由各单元上的位移不连续分量所引起的总剪应力$ \sigma _{\mathrm{S}}^i $和总正应力$ \sigma _{\mathrm{N}}^i $[17-18]可表示为：
$$ \begin{aligned} & \;\\[-6pt] & \qquad\qquad\left\{\begin{array}{cc}{\sigma }_{{\mathrm{S}}}^{i}=\displaystyle\sum _{j=1}^{n}\left({{\boldsymbol{A}}}_{{\mathrm{SS}}}^{ij}{D}_{{\mathrm{S}}}^{j}+{{\boldsymbol{A}}}_{{\mathrm{SN}}}^{ij}{D}_{{\mathrm{N}}}^{j}\right)& \;\;\qquad\quad\left(1\right)\\ {\sigma }_{{\mathrm{N}}}^{i}=\displaystyle\sum _{j=1}^{n}\left({{\boldsymbol{A}}}_{{\mathrm{NS}}}^{ij}{D}_{{\mathrm{S}}}^{j}+{{\boldsymbol{A}}}_{{\mathrm{NN}}}^{ij}{D}_{{\mathrm{N}}}^{j}\right)& \;\;\qquad\quad\left(2\right)\end{array} \right. \end{aligned}$$ 式中：$ {\boldsymbol{A}}_{{\mathrm{SS}}}^{ij} $、$ {\boldsymbol{A}}_{{\mathrm{SN}}}^{ij} $、$ {\boldsymbol{A}}_{{\mathrm{NS}}}^{ij} $、$ {\boldsymbol{A}}_{{\mathrm{NN}}}^{ij} $为单元j对单元i的影响系数矩阵；$ D_{\text{S}}^j $、$ D_{\mathrm{N}}^j $分别为j单元在局部坐标系中切向和法向位移不连续量。
水力裂缝受远场地应力和流体压力的共同作用，假设压裂液沿裂缝壁面的滤失行为满足卡特滤失方程，裂缝扩展满足最大拉应力准则，根据单元体的平衡方程可得裂缝单元表面的应力分布，即：
$$\begin{split} \begin{array}{cc}\displaystyle\sum _{j=1}^{n}\left({{\boldsymbol{A}}}_{{\mathrm{SS}}}^{ij}{D}_{{\mathrm{S}}}^{j}+{{\boldsymbol{A}}}_{{\mathrm{SN}}}^{ij}{D}_{{\mathrm{N}}}^{j}\right) = {\sigma }_{{\mathrm{S}}}^{i} = {f}_{{\mathrm{S}}}^{i} - \dfrac{1}{2}\left({\sigma }_{{\mathrm{h}}}-{\sigma }_{{\mathrm{H}}}\right)\mathrm{sin}\;2\theta \end{array} \end{split} $$ (3) $$\begin{split} &\begin{gathered} \displaystyle\sum _{j=1}^{n}\left({{\boldsymbol{A}}}_{{\mathrm{NS}}}^{ij}{D}_{{\mathrm{S}}}^{j}+{{\boldsymbol{A}}}_{{\mathrm{NN}}}^{ij}{D}_{{\mathrm{N}}}^{j}\right)={\sigma }_{{\mathrm{N}}}^{i}=\\ {p}_{i}-\left({\sigma }_{{\mathrm{H}}}{\mathrm{cos}}^{2}{\theta }_{i}+{\sigma }_{{\mathrm{h}}}{\mathrm{sin}}^{2}{\theta }_{i}\right) \end{gathered}\\[-16pt]& \end{split}$$ (4) 式中：θi为单元i与x轴正向的夹角，rad；pi为单元i承受的流体压力，MPa；σH、σh分别为水平最大和最小主应力，MPa；$ f_{\text{S}}^i $为裂缝闭合时作用在单元i上的剪应力，MPa；其表达式为：
$$ \begin{array}{cc}{f}_{{\mathrm{S}}}^{i}\leqslant |\tau {|}_{\mathrm{max}}=\left|\lambda \left({\sigma }_{{\mathrm{N}}}^{i}-{p}_{i}\right)\right| \end{array} $$ (5) 式中：$\tau $为裂缝面剪应力，MPa；λ为裂缝面的摩擦系数。
当裂缝张开时，表面间不存在摩擦，$ f_{\text{S}}^i $=0。
当裂缝张开时，裂缝内部压裂液流动满足幂律流体平板流动方程[17-18]：
$$ \begin{array}{*{20}{c}} {\dfrac{{\partial p}}{{\partial s}} = - {2^{n + 1}}\mu {{\left( {\dfrac{{1 + 2n}}{n}} \right)}^n}\dfrac{1}{{{{(w + \overline \omega )}^{2n + 1}}}}\dfrac{q}{H}{{\left| {\dfrac{q}{H}} \right|}^{n - 1}}} \end{array} $$ (6) 式中：s为沿着裂缝路径上的距离，m；w为裂缝面的本位宽度，m；$\overline \omega $为平均宽度，m；p为流体压力，MPa；n、μ分别为流体幂律指数和黏度系数，无量纲；q为裂缝中的流体沿裂缝横截面的流动速度，m3/s；H为水力裂缝高度，m。
由质量守恒定理可知，一定时间内流入岩石内部流体质量等于内部流体增加量与流体流出量之和，通过推导可以得到流体渗流连续性方程为[19]：
$$ \begin{array}{*{20}{c}} {\dfrac{{\partial q(s,t)}}{{\partial s}} + {q_{\mathrm{L}}}(s,t) + \dfrac{{\partial A(s,t)}}{{\partial t}} = 0} \end{array} $$ (7) 式中：qL为水力裂缝滤失速度，m2/s；A为水力裂缝的横截面积，m2；t为时间，s。
采用牛顿迭代法对上述方程组进行耦合求解，得到当前时间各单元的位移不连续量，上述裂缝扩展问题的边界条件为：
$$ \left\{ {\begin{array}{*{20}{l}} {q(s = 0,t) = {Q_{\mathrm{c}}}} \\ {w\left( {s = {L_{\mathrm{f}}},t} \right) = 0} \end{array}} \right. $$ 式中：Lf为缝长，m；Qc为流量，m3/s。
裂缝尖端的应力强度因子可由裂缝尖端单元的不连续位移计算得到：
$$ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{l}} {{K_{\text{I}}}} \\ {{K_{{\text{II}}}}} \end{array}} \right] = \dfrac{G}{{2(1 - \nu )\sqrt {{r_0}} }}\left[ {\begin{array}{*{20}{c}} {D_{\mathrm{N}}^{{\mathrm{tip}}}} \\ {D_{\mathrm{S}}^{{\mathrm{tip}}}} \end{array}} \right]} \end{array} $$ (8) 式中，KⅠ、KⅡ分别为Ⅰ型和Ⅱ型应力强度因子；G为剪切模量，MPa；v为泊松比；r0为裂缝尖端单元的半长，m；$ D_{\mathrm{S}}^{{\mathrm{tip}}} $、$ D_{\mathrm{N}}^{{\mathrm{tip}}} $分别表示为裂缝尖端单元的切向、法向位移不连续量，m。
通过裂缝尖端的应力强度因子计算其等效应力强度因子，当裂缝尖端的应力强度因子大于断裂韧性时，裂缝发生扩展[20]，且裂缝扩展方向$\theta _0 $为：
$$ \begin{split} &\begin{gathered} {\theta _0} = \left\{ {\begin{array}{*{20}{l}} {0}\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\; \ {{K_{{\text{II}}}} = 0} \\ {2\arctan \left\{ {\dfrac{1}{4}\left[ {\dfrac{{{K_{\text{I}}}}}{{{K_{{\text{II}}}}}} - {{\mathrm{sgn}}} \left( {{K_{{\text{II}}}}} \right) \sqrt {{{\left( {\dfrac{{{K_{\text{I}}}}}{{{K_{{\text{II}}}}}}} \right)}^2} + 8} } \right]} \right\}}\quad{{K_{{\text{II}}}} \ne 0}\\ {\mathop {{70.6}}\nolimits^\circ }\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad{{K_{\text{I}}} = 0} \end{array}} \right. \end{gathered}\\& \end{split}$$ (9) 裂缝单元随着水力裂缝扩展而增加，计算各裂缝单元位移不连续量及其流体压力，循环计算模拟水力裂缝动态扩展过程。
在地层模型基础上，根据裂缝形态参数，采用非结构化网格对产能模型进行划分，建立的单井产能模型如图3所示。选择气、水两相黑油模型，使用Intersect油藏数值模拟器进行压后产能模拟。
参照韩城区块现场资料，在垂向上建立了3层尺寸为500 m×500 m×50 m的模型，从上到下分别对应顶板层、煤储层、高含水底板层，模型采取非结构化网格划分，设置目标直井11#煤层埋深为1 190~1 200 m，顶板深度为1 170~1 190 m，底板深度为1 200~1 220 m，模拟射孔位置为顶板（深度1 184.0~1 185.0 m）、顶板+煤层（深度1 189.5~1 190.5 m）、煤层（深度1 194~1 195 m），射孔密度16孔/m，射孔直径10 mm，90°相位角螺旋布孔，采用活性水压裂体系，粒径为0.212~0.425 mm与0.3~0.6 mm的石英砂组合，施工排量8 m3/min，注入液量900 m3，支撑剂50 m3。模型的岩石力学参数见表1。
表 1 岩石力学参数Table 1. Rock mechanics parameters参数 顶板 煤层 底板 抗拉强度/MPa 4.5 1.0 3.5 杨氏模量/GPa 15 6.5 18 泊松比 0.25 0.35 0.25 渗透率/10−3μm2 0.1 0.1 0.1 地层孔隙度/% 1 5 10 孔隙压力/MPa 4 4 4 垂向地应力/MPa 16 15 17 最小水平主应力/MPa 15 14 16 最大水平主应力/MPa 17 16 18 Langmuir体积/（m3·t−1） — 22 — Langmuir压力/MPa — 2.5 — 临界解吸压力/MPa — 3.5 — 压缩系数/MPa−1 0.02 0.05 0.03 密度/（kg·m−3） 2800 1400 2500 由于研究区域高含水底板与煤层距离1~15 m，因此每种压裂位置设计4种模拟方案A1/A2、B1/B2、C1/C2、D1/D2，分别表示煤储层距含水层1、5、10、15 m时气井产气/产水量，设定井底压降速率为0.01 MPa/d。压裂方案示意图如图4所示，压裂模拟后再进行产能模拟，模拟不同条件下的产气量及产水量。
以A井为例，该井储层物性条件及施工参数与模型设置相似，压裂位置为煤层，高含水层距离煤层为1 m，根据压力拟合产量，拟合效果较好，说明建立的产能模型较为可靠。
3. 结果分析
3.1 顶板射孔压裂对产水产气的影响
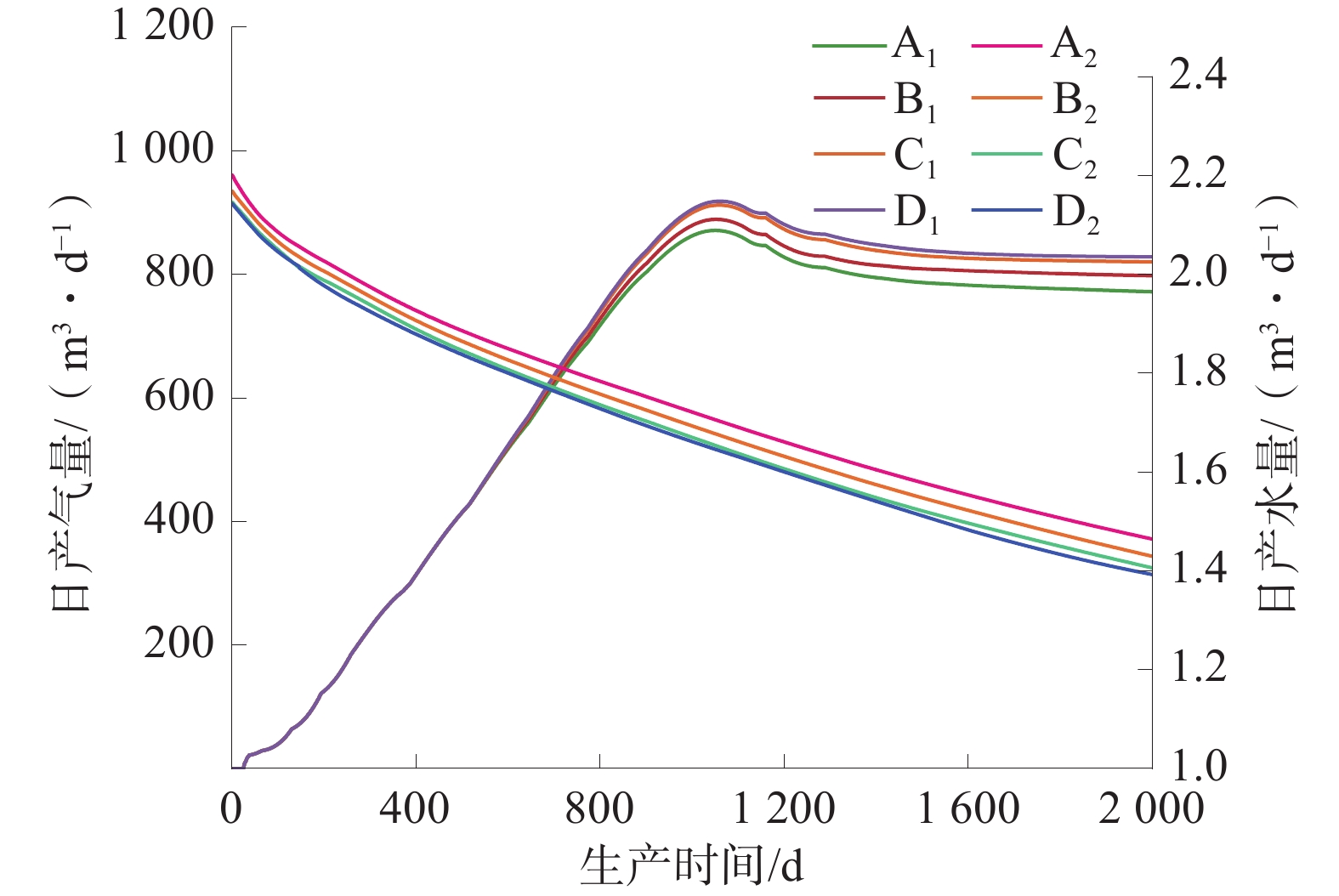
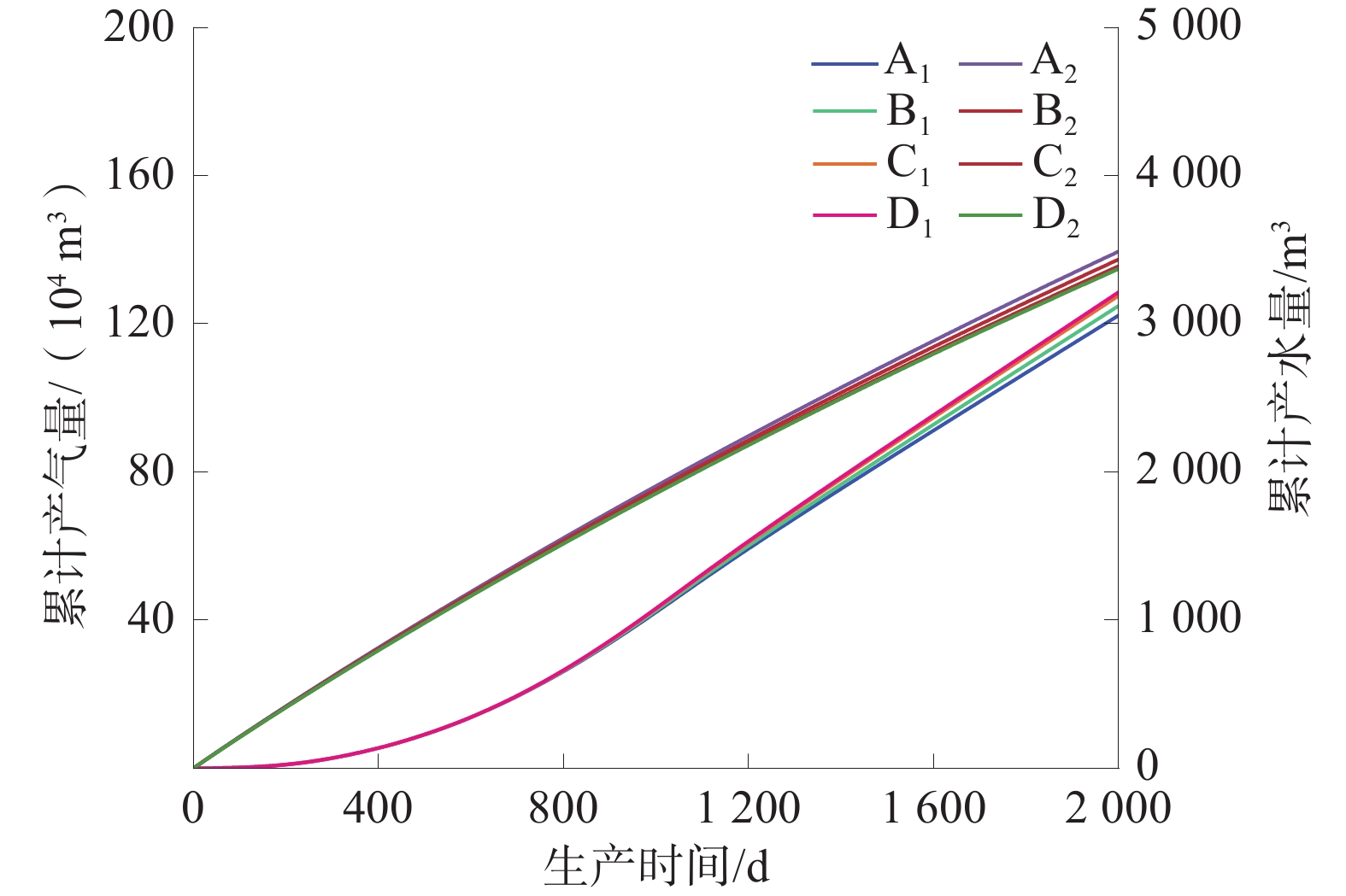
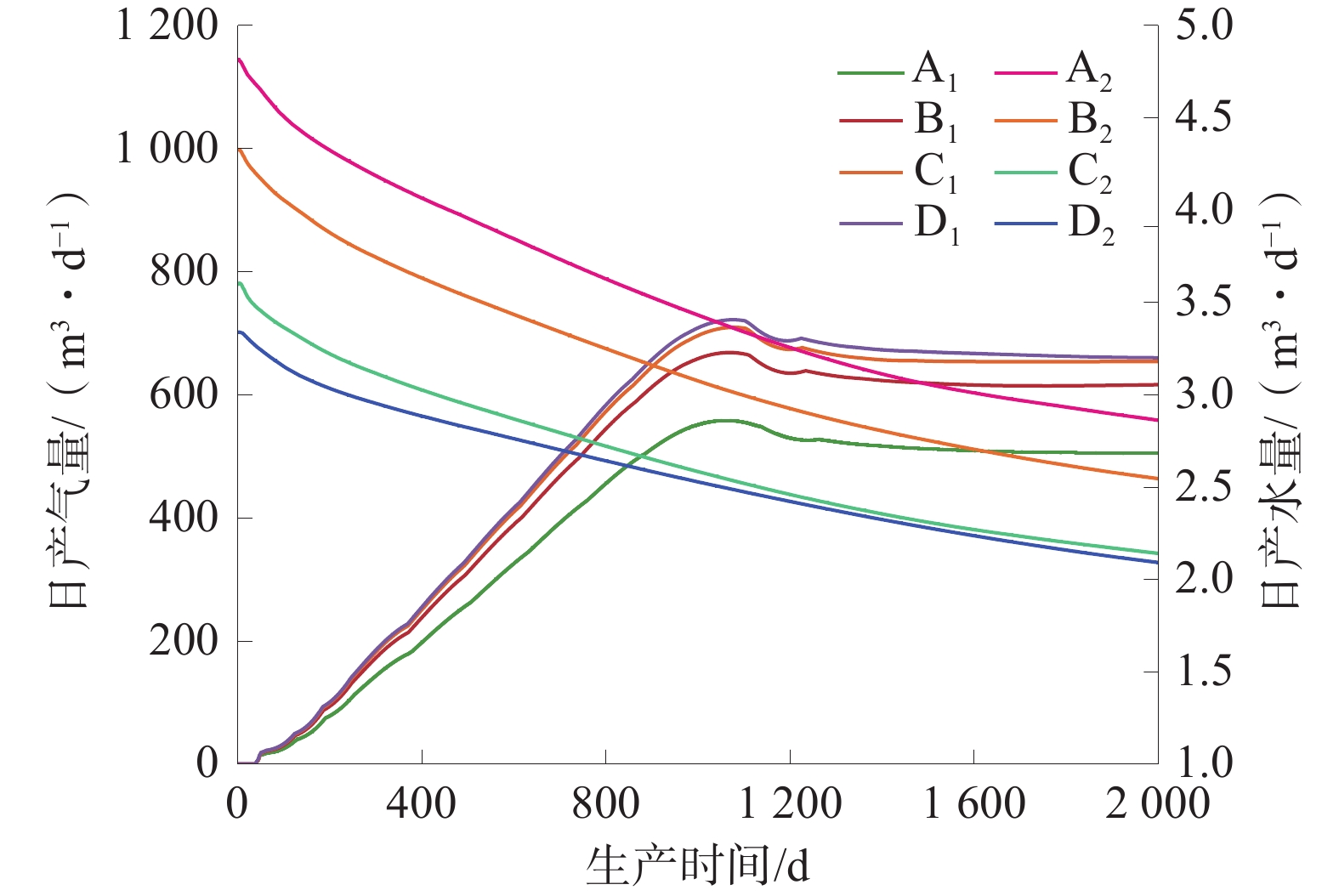
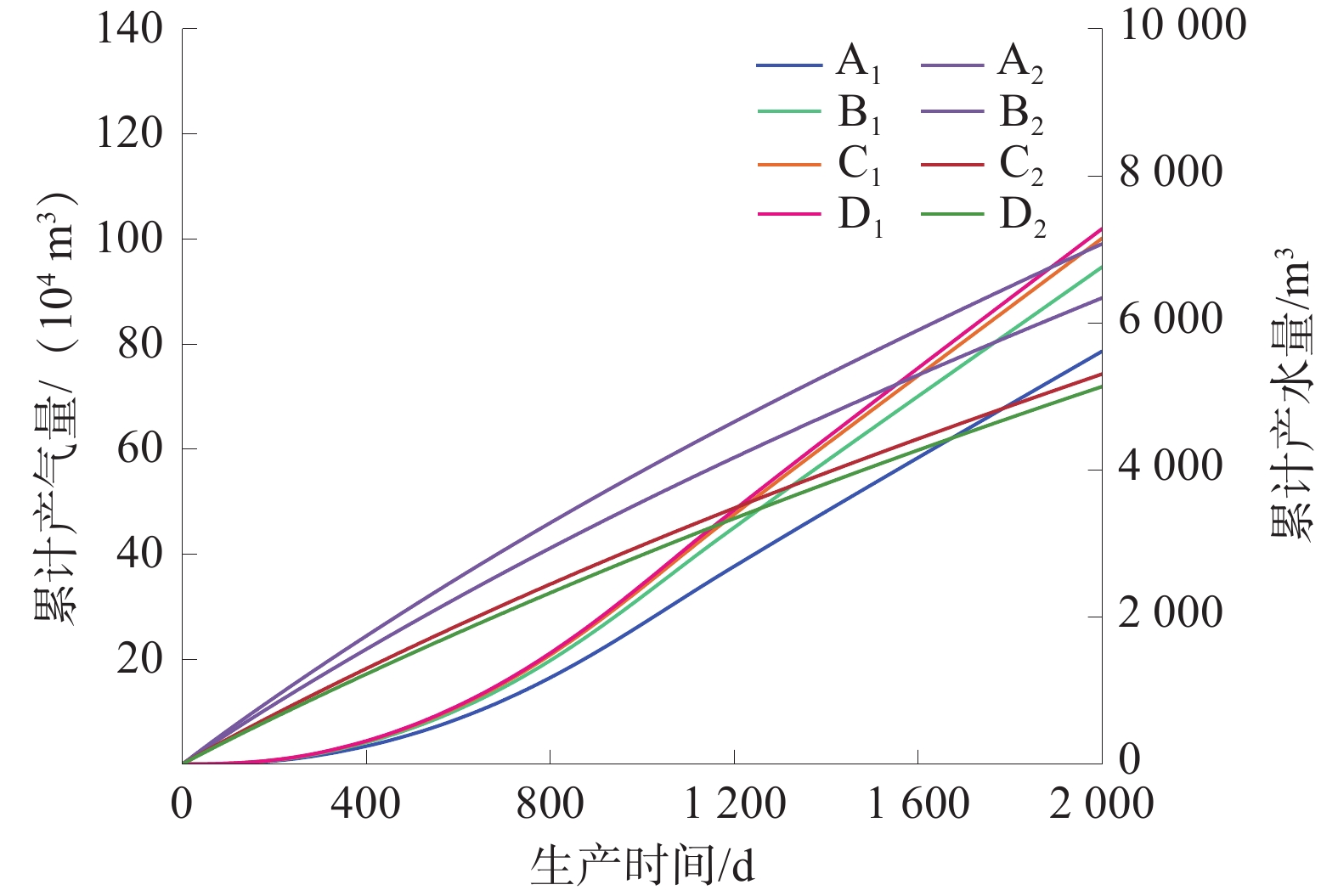
模拟了煤储层与高含水底板层不同距离情况下，顶板压裂改造后气井产气产水结。顶板压裂气井日产气量、日产水量如图5所示，顶板压裂气井累计产气量、累计产水量如图6所示。
![]()
图 6 顶板压裂气井累计产气量、累计产水量Figure 6. Cumulative gas and water volume of roof fractured gas well整体来看，模拟案例的产气量、产水量变化较小，其产气特征可分为3个阶段：①初期仅产水阶段，此时气体分子仍然吸附在多孔介质内，随着地层水的不断排出，储层压力降低，当达到气体临界解吸压力时，气体分子解吸产出；②产气上升阶段，此时地层压降漏斗逐渐扩大，解吸的气体也不断增加；③稳产阶段，此时经过长期排水，产气量、产水量逐渐趋于稳定。
4类模拟结果显示，气井见气时间、产气峰值时间、稳产气量、累计产气量、累计产水量最大差异率分别为13.33%、1.22%、6.83%、5.47%、3.68%，差异率较小，表明含水层对于顶板压裂方式产量几乎无影响。分析其主要原因为：①顶板压裂时水力裂缝主要在顶板中扩展并波及煤层，在顶板与煤层间形成破碎带，在支撑剂支撑作用下形成“高速渗流通道”，煤粉在重力作用下不易向上流动堵塞孔道，煤层气分子则能够自由向上部渗流；②支撑剂铺置在裂缝底部能形成1种人工隔层，一定程度上增大了层间应力差，避免裂缝过度向煤层延伸，可使水力裂缝沿横向扩展延伸形成高导流长缝。因此，底板高含水的情况对顶板压裂方式产气及产水量影响较弱，碎软煤层应用顶板压裂方式产量较好。
3.2 顶板+煤层射孔压裂对产水产气的影响
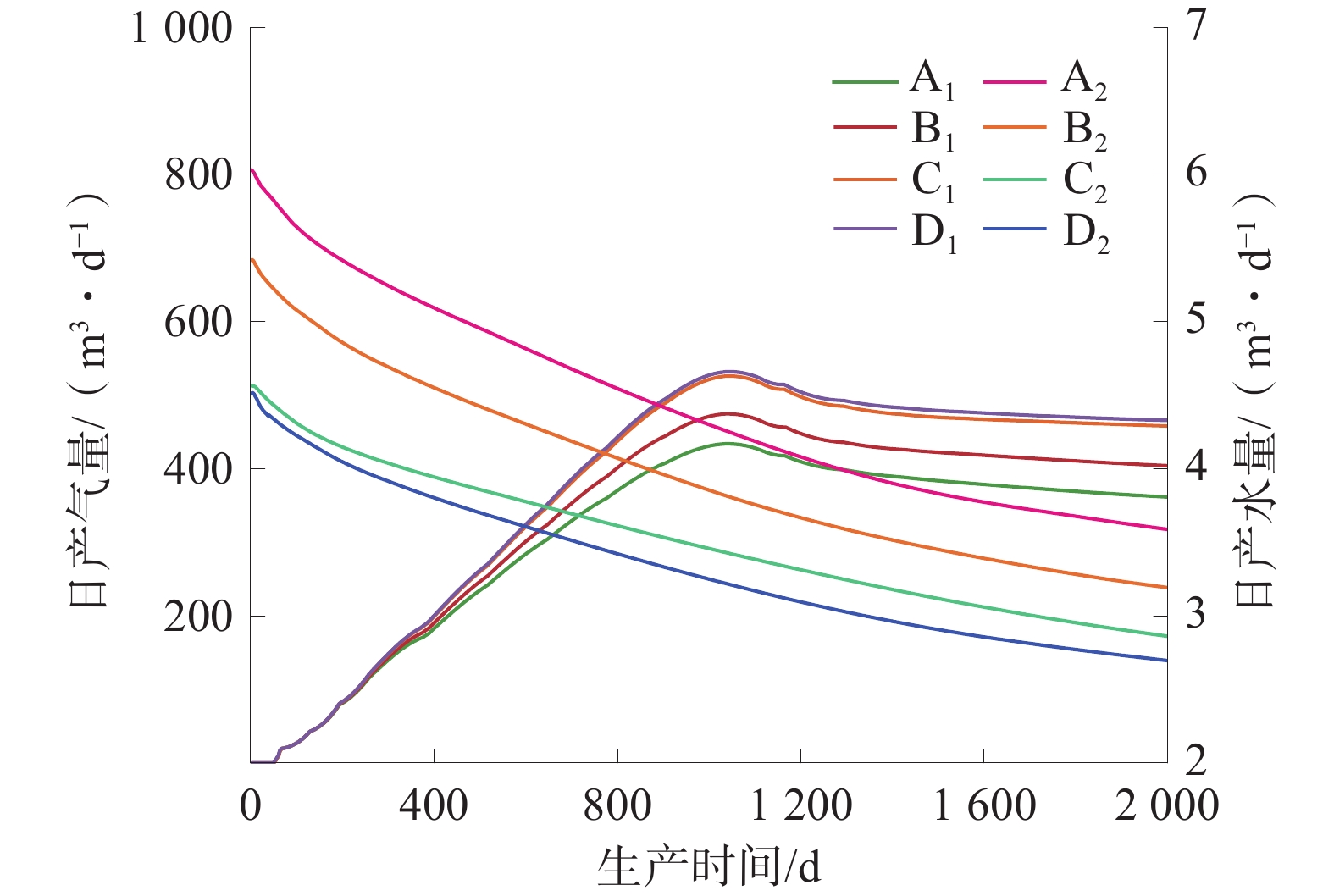
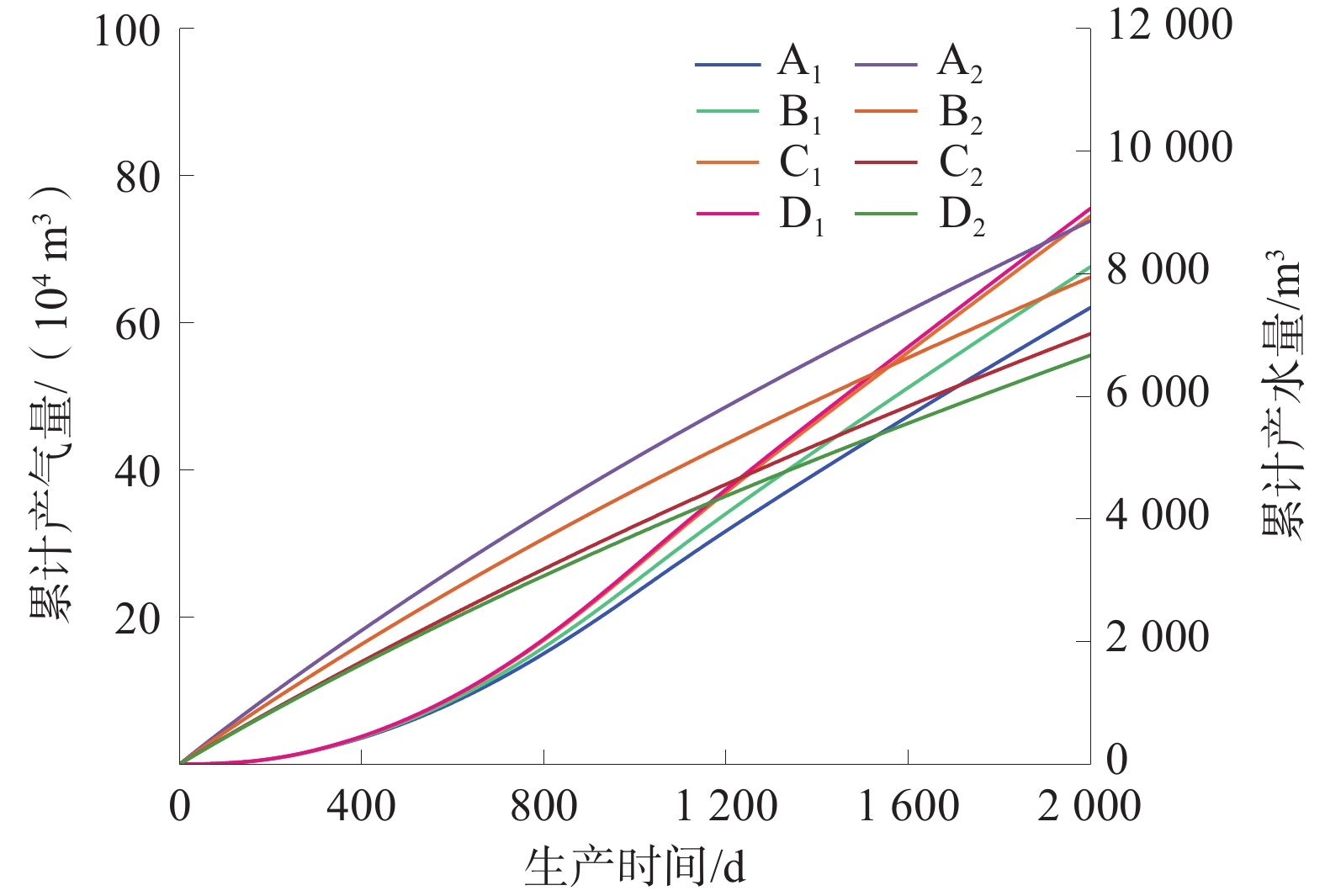
顶板压裂及煤层压裂方式应对不同地层条件各有优点，为定量表征其变化规律，模拟了顶板+煤层射孔压裂产水产气能力。顶板+煤层压裂气井日产气量、日产水量如图7所示、顶板+煤层压裂气井累计产气量、累计产水量如图8所示。
![]()
图 7 顶板+煤层压裂气井日产气量、日产水量Figure 7. Daily gas and water volume of roof and coal seam fractured well![]()
图 8 顶板+煤层压裂气井累计产气量、累计产水量Figure 8. Cumulative gas and water volume of roof and coal seam fractured well4类模拟结果显示，气井见气时间、产气峰值时间、稳产气量、累计产气量、累计产水量最大差异率分别为18.75%、1.58%、24.15%、23.13%、37.71%，差异率升高，表明含水层对于顶板+煤层压裂方式产量有一定影响。
与顶板压裂方式相比，煤层+顶板压裂方式产气产水变化趋势一致，见气时间增加了33.33%~37.5%；产气峰值时间增加了1.04%~1.67%；稳产气量降低24.57%~53%，累计产气量降低20.55%~35.39%，累计产水量增加53.63%~104.06%，整体产量变化较为明显，尤其是煤储层距含水层1、5 m时，累计产气量分别降低35.39%与23.81%，累计产水量分别增加104.06%与85.79%。这是由于煤层厚度较小，水力裂缝易压穿煤层并沟通高含水底板层，底板中的地层水沿裂缝通道涌入井筒，导致排水降压效率降低，大量地层水的产出也导致煤粉颗粒剥离效果增强，煤粉随地层水一起流动并沉积、堵塞生产通道导致产量降低。当煤储层距含水层10~15 m时，产量变化幅度降低，表明此时缝高未达到高含水底板层或仅有少量裂缝沟通，气井额外产水量及煤粉剥离程度均较低。
顶板+煤层压裂方式整体产气量低于顶板压裂方式，分析认为顶板+煤层压裂时，裂缝将在煤层顶板、顶板与煤层界面、煤层、底板内扩展，而11#煤层应力较低，压裂液优先进入低应力的煤层射孔簇，顶板射孔簇进液相对较少，裂缝在顶板扩展延伸程度有限，易沿煤层延伸扩展形成短宽缝以及增加沟通高含水层的风险，导致改造效果不佳而降低产量。
3.3 煤层射孔压裂对产水产气的影响
模拟了煤储层与含水层不同距离下煤层压裂方式的产水产气能力。煤层压裂气井日产气量、日产水量如图9所示，煤层压裂气井累计产气量、累计产水量结果如图10所示。
![]()
图 9 煤层压裂气井日产气量、日产水量Figure 9. Daily gas and water volume of coal seam fractured gas well![]()
图 10 煤层压裂气井累计产气量、累计产水量Figure 10. Cumulative gas and water volume of roof and coal seam fractured gas well由模拟结果可知，煤层直接压裂其产量特征与顶板压裂、顶板+煤层压裂一致，但整体产气量最低，产水量最高。
煤层直接压裂与顶板+煤层压裂相比，见气时间增加18.18%~22.92%，产气峰值时间降低2.51%~3.16%，累计产气量降低23.54%~30.6%；累计产水量增加25.29%~32.5%，稳产气量降低44.05%~55.98%，表明煤层直接压裂产气量低于顶板+煤层压裂，水力裂缝沟通高含水底板层程度更高。
煤层直接压裂与顶板压裂相比，见气时间延长了48%~49.15%，产气峰值时间降低了1.15%~1.45%，累计产气量降低42.28%~50.6%，累计产水量增加99.44%~155.67%，稳产气量降低79.45%~120.54%，呈现出见气时间晚、低产气、高产水的特点，与顶板压裂方式产量差距更大。
分析碎软煤层直接压裂效果较差的原因为：
1）碎软煤层直接压裂时，对煤体结构造成的破坏较大，同时地层流体流经煤粉颗粒会也对其产生阻力作用，包括摩擦阻力和压差阻力。流体流速越大，对煤粉的拖曳力以及上举力越大，更容易导致煤粉颗粒由基质岩体剥离，并随流体运移、沉积堵塞孔道，降低储层渗透率。
2）碎软煤层机械强度较低，水力裂缝向前延伸较为困难，在纵向上扩展程度相对较高，由于煤层底板水动力条件活跃，水力裂缝沟通高含水层后泄流半径扩展速度、压降纵向扩展速度降低，相同排采时间达到临界解吸压力的区域越小，增加了排水降压的难度，由此不利于煤层气井的高产稳产。
3）碎软煤层割理裂隙较为发育，直接压裂时压裂液易产生大量滤失，压裂液效率较低；而直接压裂易形成短宽缝，导致支撑剂在近井地带大量沉降，增加砂堵的风险，无法在缝网内形成有效支撑，降低压裂改造效果。
4. 矿场试验
数值模拟表明煤层与高含水不同距离下的压裂位置选取对于产量有重要影响，为验证数值模拟的结果，收集韩城区块14口煤层气井资料，其生产层位均为11#煤层，在煤层、顶板、顶板+煤层进行压裂，液体体系为活性水+清洁压裂液，支撑剂为0.3~0.6 mm与0.212~0.425 mm石英砂组合，施工排量8~10 m3/min，注入液量900~1 000 m3，支撑剂量为50~70 m3，煤层与高含水砂岩层距离为3.5~15 m。煤层与高含水砂岩层不同距离与气井产量关系见表2。
表 2 煤层与高含水砂岩层不同距离与气井产量关系Table 2. Relationship between different distance of coal seam and sandstone layer with high water content and gas well output序号 井号 压裂位置 煤层与高含水
砂岩层距离/m日产气量/
m3日产水量/
m31 H-1 煤层 8.0 313 9.00 2 H-2 15.0 365 1.60 3 H-3 4.0 218 10.10 4 H-4 5.0 255 11.70 5 H-5 7.3 330 7.00 7 H-7 3.5 170 13.00 8 H-8 13.0 376 4.00 9 H-9 顶板 11.0 928 0.50 10 H-10 4.50 825 0.15 11 H-11 7.0 863 0.43 12 H-12 顶板+煤层 5.4 315 9.40 13 H-13 12.0 374 5.60 14 H-14 10.0 340 6.40 通过表2可以看出，顶板压裂受高含水底板影响较小，产量变化幅度小，而对顶板+煤层压裂以及煤层压裂有较大影响。
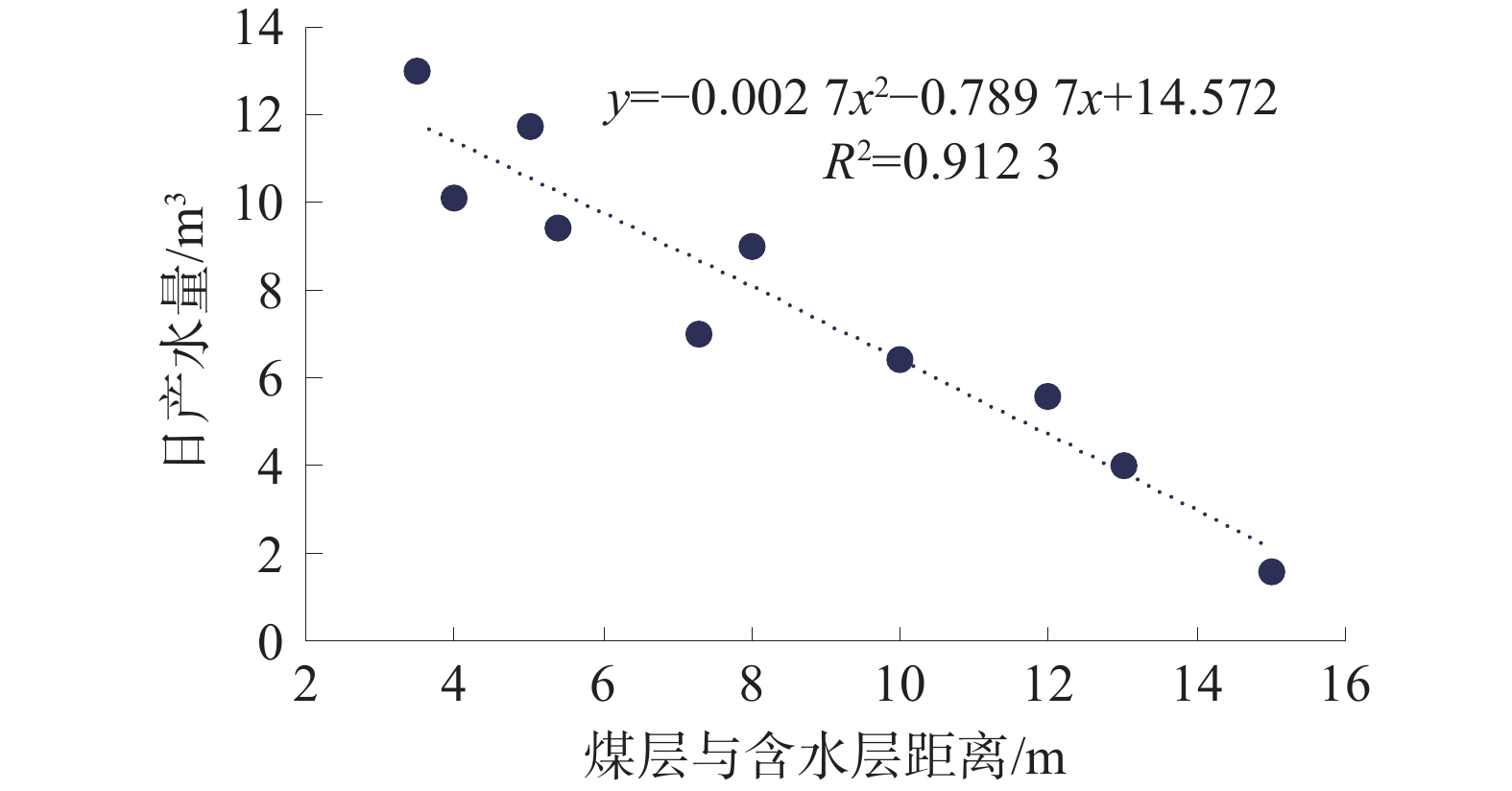
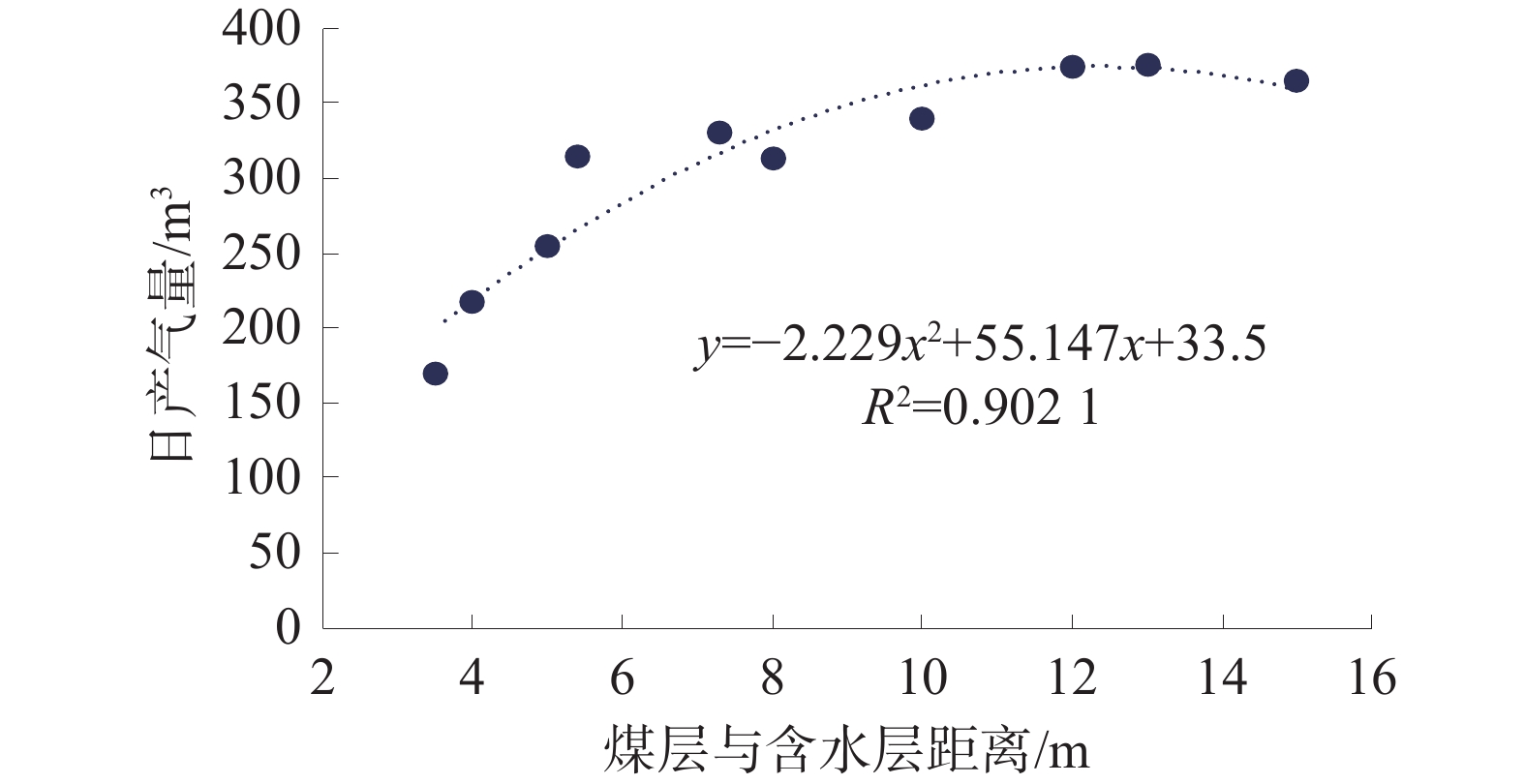
将煤层压裂、顶板+煤层压裂方式产气及产水量绘制于散点图内，煤层、顶板+煤层压裂时煤层与含水层距离与日产水量关系如图11所示，煤层、顶板+煤层压裂时煤层与含水层距离与日产气量关系如图12所示。
![]()
图 11 煤层、顶板+煤层压裂时煤层与含水层距离与日产水量关系Figure 11. Relationship between distance of coal seam and aquifer and daily water production during fracturing of coal seam, roof + coal seam从整体来看，随着煤层与含水层距离增加，2种压裂方式产气量也随之增加，产水量逐渐降低；当含水层与煤层距离在10 m以下时，2种压裂方式易沟通高含水层，导致大量产水而产气量较低；在10~15 m时，产气量变化逐渐趋于平稳，产水量较低。不同压裂位置产气量关系为：顶板压裂＞顶板+煤层压裂＞煤层压裂。该产气特征与模拟结果基本一致。
![]()
图 12 煤层、顶板+煤层压裂时煤层与含水层距离与日产气量关系Figure 12. Relationship between distance of coal seam and aquifer and daily gas production during fracturing of coal seam, roof + coal seam因此，当韩城区块11#煤层进行压裂改造时，首先应判断高含水底板砂岩层与煤储层的距离，当含水层距离小于10 m时，模拟结果显示顶板+射孔压裂与煤层直接压裂产水量较高，对排水降压开采影响较大，产气量较低，应选择在顶板处压裂；当含水层距离大于10 m时，高含水层对3种压裂方式影响较小，此时应判断是否具有顶板压裂的条件，优先选择在顶板处压裂，当不具备顶板压裂条件时，若煤储层物性参数好、原生结构煤发育时也可选择顶板+煤层压裂与煤层直接压裂方式。
5. 结 语
1）数值模拟及现场应用结果表明：当高含水层与煤储层距离在1~5 m时，产量与含水层距离呈线性关系，距离高含水层越近，沟通高含水底板层程度越高，产气量越低；当距离处于10~15 m时，产量变化趋势逐渐变缓，高含水层对压裂方式的影响减弱。
2）对比3种压裂位置方案：①在产气方面，顶板压裂>顶板+煤层压裂＞煤层压裂；②产水方面，煤层压裂>顶板+煤层压裂＞顶板压裂。顶板+煤层压裂及煤层压裂增加了对煤体结构的破坏程度导致煤粉颗粒剥离堵塞孔道而降低产量；顶板压裂方式整体呈现高产气、低产水的特征，见气时间短，稳产期长，受底板高含水层的影响小，对煤体结构破坏程度低，更适合此类地层开发。
-
![]()
图 6 顶板压裂气井累计产气量、累计产水量
Figure 6. Cumulative gas and water volume of roof fractured gas well
![]()
图 7 顶板+煤层压裂气井日产气量、日产水量
Figure 7. Daily gas and water volume of roof and coal seam fractured well
![]()
图 8 顶板+煤层压裂气井累计产气量、累计产水量
Figure 8. Cumulative gas and water volume of roof and coal seam fractured well
![]()
图 9 煤层压裂气井日产气量、日产水量
Figure 9. Daily gas and water volume of coal seam fractured gas well
![]()
图 10 煤层压裂气井累计产气量、累计产水量
Figure 10. Cumulative gas and water volume of roof and coal seam fractured gas well
![]()
图 11 煤层、顶板+煤层压裂时煤层与含水层距离与日产水量关系
Figure 11. Relationship between distance of coal seam and aquifer and daily water production during fracturing of coal seam, roof + coal seam
![]()
图 12 煤层、顶板+煤层压裂时煤层与含水层距离与日产气量关系
Figure 12. Relationship between distance of coal seam and aquifer and daily gas production during fracturing of coal seam, roof + coal seam
表 1 岩石力学参数
Table 1 Rock mechanics parameters
参数 顶板 煤层 底板 抗拉强度/MPa 4.5 1.0 3.5 杨氏模量/GPa 15 6.5 18 泊松比 0.25 0.35 0.25 渗透率/10−3μm2 0.1 0.1 0.1 地层孔隙度/% 1 5 10 孔隙压力/MPa 4 4 4 垂向地应力/MPa 16 15 17 最小水平主应力/MPa 15 14 16 最大水平主应力/MPa 17 16 18 Langmuir体积/（m3·t−1） — 22 — Langmuir压力/MPa — 2.5 — 临界解吸压力/MPa — 3.5 — 压缩系数/MPa−1 0.02 0.05 0.03 密度/（kg·m−3） 2800 1400 2500 
下载: 导出CSV
表 2 煤层与高含水砂岩层不同距离与气井产量关系
Table 2 Relationship between different distance of coal seam and sandstone layer with high water content and gas well output
序号 井号 压裂位置 煤层与高含水
砂岩层距离/m日产气量/
m3日产水量/
m31 H-1 煤层 8.0 313 9.00 2 H-2 15.0 365 1.60 3 H-3 4.0 218 10.10 4 H-4 5.0 255 11.70 5 H-5 7.3 330 7.00 7 H-7 3.5 170 13.00 8 H-8 13.0 376 4.00 9 H-9 顶板 11.0 928 0.50 10 H-10 4.50 825 0.15 11 H-11 7.0 863 0.43 12 H-12 顶板+煤层 5.4 315 9.40 13 H-13 12.0 374 5.60 14 H-14 10.0 340 6.40
下载: 导出CSV
-
[1] 徐凤银,侯伟,熊先钺,等. 中国煤层气产业现状与发展战略[J]. 石油勘探与开发,2023,50(4):669−682. XU Fengyin, HOU Wei, XIONG Xianyue, et al. The status and development strategy of coalbed methane industry in China[J]. Petroleum Exploration and Development, 2023, 50(4): 669−682.
[2] 郭智栋,王玉斌,鲍园,等. 韩城地区煤层气成因类型及微生物开发潜力[J]. 西安科技大学学报,2023,43(3):539−548. GUO Zhidong, WANG Yubin, BAO Yuan, et al. Coalbed methane generation and microbial-development potential in Hancheng Block[J]. Journal of Xi’an University of Science and Technology, 2023, 43(3): 539−548.
[3] 王双明,申艳军,宋世杰,等. “双碳”目标下煤炭能源地位变化与绿色低碳开发[J]. 煤炭学报,2023,48(7):2600−2612. WANG Shuangming, SHEN Yanjun, SONG Shijie, et al. Change of coal energy status and green and low-carbon development under the “dual carbon” goal[J]. Journal of China Coal Society, 2023, 48(7): 2600−2612.
[4] 黄中伟,李国富,杨睿月,等. 我国煤层气开发技术现状与发展趋势[J]. 煤炭学报,2022,47(9):3212−3238. HUANG Zhongwei, LI Guofu, YANG Ruiyue, et al. Review and development trends of coalbed methane exploitation technology in China[J]. Journal of China Coal Society, 2022, 47(9): 3212−3238.
[5] 贾慧敏,胡秋嘉,樊彬,等. 沁水盆地郑庄区块北部煤层气直井低产原因及高效开发技术[J]. 煤田地质与勘探,2021,49(2):34−42. JIA Huimin, HU Qiujia, FAN Bin, et al. Causes for low CBM production of vertical wells and efficient development technology in northern Zhengzhuang Block in Qinshui Basin[J]. Coal Geology & Exploration, 2021, 49(2): 34−42.
[6] 李俊峰. 沁水盆地郑庄井田煤层气分段压裂水平井开发技术[J]. 煤矿安全,2023,54(6):34−40. LI Junfeng. Development technology of coalbed methane horizontal wells with staged fracturing in Zhengzhuang Field of Qinshui Basin[J]. Safety in Coal Mines, 2023, 54(6): 34−40.
[7] 李全中,倪小明,胡海洋. 煤层气直井压裂规模对排采典型指标的影响[J]. 煤矿安全,2021,52(5):182−187. LI Quanzhong, NI Xiaoming, HU Haiyang. Influence of fracturing scale of CBM vertical well on typical indexes of drainage and mining[J]. Safety in Coal Mines, 2021, 52(5): 182−187.
[8] 胡秋嘉,毛崇昊,樊彬,等. 高煤阶煤层气井储层压降扩展规律及其在井网优化中的应用[J]. 煤炭学报,2021,46(8):2524−2533. HU Qiujia, MAO Chonghao, FAN bin, et al. Review and development trends of coalbed methane exploitation technology in China: Pressure drop expansion law of high rank coalbed methane reservoir and its application in well pattern optimization[J]. Journal of China Coal Society, 2021, 46(8): 2524−2533.
[9] 赵馨悦,韦波,袁亮,等. 煤储层水文地质特征及其煤层气开发意义研究综述[J]. 煤炭科学技术,2023,51(4):105−117. ZHAO Xinyue, WEI Bo, YUAN Liang, et al. Hydrological characters of coal reservoir and their significances on coalbed methane development: A review[J]. Coal Science and Technology, 2023, 51(4): 105−117.
[10] 张健,朱苏阳,彭小龙,等. 煤层气−水−固三相流动模型与数值模拟研究[J]. 中国海上油气,2022,34(1):117−127. ZHANG Jian, ZHU Suyang, PENG Xiaolong, et al. Tri-phase flow model of coalbed methane-water-solid and numerical simulation study[J]. China Offshore Oil and Gas, 2022, 34(1): 117−127.
[11] 张群,葛春贵,李伟,等. 碎软低渗煤层顶板水平井分段压裂煤层气高效抽采模式[J]. 煤炭学报,2018,43(1):150−159. ZHANG Qun, GE Chungui, LI Wei, et al. Efficient coalbed methane extraction mode of fractured soft and low permeability coal seam roof by staged fracturing horizontal well[J]. Journal of China Coal Society, 2018, 43(1): 150−159.
[12] 李曙光,王红娜,徐博瑞,等. 大宁-吉县区块深层煤层气井酸化压裂产气效果影响因素分析[J]. 煤田地质与勘探,2022,50(3):165−172. LI Shuguang, WANG Hongna, XU Borui, et al. Influencing factors on gas production effect of acid fractured CBM Wells in deep coal seam of Daning-Jixian Block[J]. Coal Geology & Exploration, 2022, 50(3): 165−172.
[13] 许耀波,朱玉双,张培河. 紧邻碎软煤层的顶板岩层水平井开发煤层气技术[J]. 天然气工业,2018,38(9):70−75. doi: 10.3787/j.issn.1000-0976.2018.09.009 XU Yaobo, ZHU Yushuang, ZHANG Peihe. Application of CBM horizontal well development technology in the roof strata close to broken-soft coal seams[J]. Natural Gas Industry, 2018, 38(9): 70−75. doi: 10.3787/j.issn.1000-0976.2018.09.009
[14] 梁智飞,刘长松,甄怀宾,等. 韩城区块煤层气井二次改造工艺优化及现场试验[J]. 石油钻探技术,2022,50(3):92−98. doi: 10.11911/syztjs.2022067 LIANG Zhifei, LIU Changsong, ZHEN Huaibin, et al. Optimization and field application of secondary stimulation technologies for coalbed methane wells in Hancheng Block[J]. Petroleum Drilling Techniques, 2022, 50(3): 92−98. doi: 10.11911/syztjs.2022067
[15] CIPOLLA C, WENG X, MACK M, et al. Integrating microseismic mapping and complex fracture modeling to characterize fracture complexity [C]// 2012 SPE/EAGE European Unconventional Resources Conference and Exhibition. SPE, 2012. ISBN:978−1−61399−189−3.
[16] WU K, OLSON J E. Simultaneous multifracture treatments: Fully coupled fluid flow and fracture mechanics for horizontal wells[J]. SPE Journal, 2015, 20(2): 337−346. doi: 10.2118/167626-PA
[17] 周治东,程万,魏子俊,等. 基于BEM的水力裂缝起裂与扩展数值模拟[J]. 地球物理学进展,2020,35(2):807−814. doi: 10.6038/pg2020DD0041 ZHOU Zhidong, CHENG Wan, WEI Zijun, et al. Numerical simulation of hydraulic fracture initiation and propagation based on BEM[J]. Progress in Geophysics, 2020, 35(2): 807−814. doi: 10.6038/pg2020DD0041
[18] 周航,周福建. 水力压裂切割煤层顶板力学机理及参数优化[J]. 科学技术与工程,2022,22(19):8253−8261. ZHOU Hang, ZHOU Fujian. Mechanical mechanism and parameter optimization of hydraulic fracturing for cutting thick roof of coal seam[J]. Science Technology and Engineering, 2022, 22(19): 8253−8261.
[19] 李越,牟建业,张士诚,等. 塔河缝洞型碳酸盐岩储层裂缝扩展规律数值模拟[J]. 中国石油大学学报(自然科学版),2022,46(6):135−142. LI Yue, MOU Jianye, ZHANG Shicheng, et al. Numerical simulation of fracture propagation law in Tahe fractured-vuggy carbonate reservoir[J]. Journal of China University of Petroleum (Edition of Natural Science), 2022, 46(6): 135−142.
[20] 金衍,程万,陈勉. 页岩气储层压裂数值模拟技术研究进展[J]. 力学与实践,2016,38(1):1−9. doi: 10.6052/1000-0879-15-225 JIN Yan, CHENG Wan, CHEN Mian. A review of numerical simulations of hydro-fracking in shale gas reservoir[J]. Mechanics in Engineering, 2016, 38(1): 1−9. doi: 10.6052/1000-0879-15-225
计量
- 文章访问数: 17
- HTML全文浏览量: 2
- PDF下载量: 4
