锚杆支护技术是1种简单有效的巷道围岩加固技术，至今有60多年的发展历程，经历了低强度向高强度、高预应力、强力支护的跨越式发展^[1]。锚杆支护是煤矿巷道的主要支护方式，对煤矿安全、高效建设与生产有着十分重要的积极作用。

锚固体力学性能对锚杆支护设计具有重要意义，众多学者对锚固体力学性能进行了大量研究。尤春安^[2]利用Mindlin位移方程，获得了全长黏结式锚杆沿杆体剪力分布的理论解；黄明华等^[3-4]基于非线性剪切滑移模型，采用荷载传递方法分析了锚固长度对锚杆受力特性的影响；李鹏飞等^[5]基于四线性黏结滑移模型，修正了前人提出的剪胀-软化-脱黏阶段、软化-脱黏阶段和完全脱黏阶段的荷载-位移解析方程；林健等^[6-7]通过实验室实验，得到了锚杆外形与锚杆锚固性能及安装阻力之间的关系；CAO等^[8-9]研究了在锚固剂中添加不同钢质骨料对锚固力的影响，发现钢质骨料有助于提高树脂锚固剂抗剪能力；姚强岭等^[10]、尹延春等^[11]研究了锚固段应力分布演化规律，锚杆轴力沿着锚固段逐渐减小，而剪应力是先增大，达到峰值后减小；韩军等^[12]通过室内试验，得到了不同强度围岩锚固力学机理；宋义敏等^[13]研究了锚固体系传力规律，发现拉拔力沿锚固方向由锚固端部开始向深部传递，并且随着拉拔力增加变形集中区域由锚固端部沿锚固方向向深部扩展；赵同彬等^[14]采用PFC颗粒流软件对锚杆界面力学试验进行模拟，为锚固机理的细观尺度研究提供了可行性；马双文等^[15]采用ANSYS对锚杆拉拔试验进行模拟，研究了锚杆横肋间距对锚固效果的影响；李东印等^[16]利用 ABAQUS 对全长黏结式螺纹钢锚杆拉拔过程采用二维平面建模研究，研究了螺纹钢横肋几何参数对锚固体失效形式的影响；刘亚鑫等^[17]基于ABAQUS界面黏结损伤模型，研究了锚固界面力学行为。

我国煤炭的开采深度正在逐年递加，煤矿巷道遇到强采动、大变形等工程难题的概率也提高了，这就要求锚杆支护对围岩提供越来越高的锚固承载特性。尤春安等^[18]提出，锚固承载力的大小主要取决于锚固段的失效形式，认为锚固体主要有以下4种失效形式：锚杆体的断裂、锚杆体与灌浆体产生滑脱、锚杆体与灌浆体产生滑脱、岩土体破坏。为此，根据已开展的锚杆拉拔模型试验^[19]，在以往研究的基础上，利用有限元软件ABAQUS，对不同锚杆肋间距锚固体的失效形式进行数值模拟研究。

1.   黏聚力单元

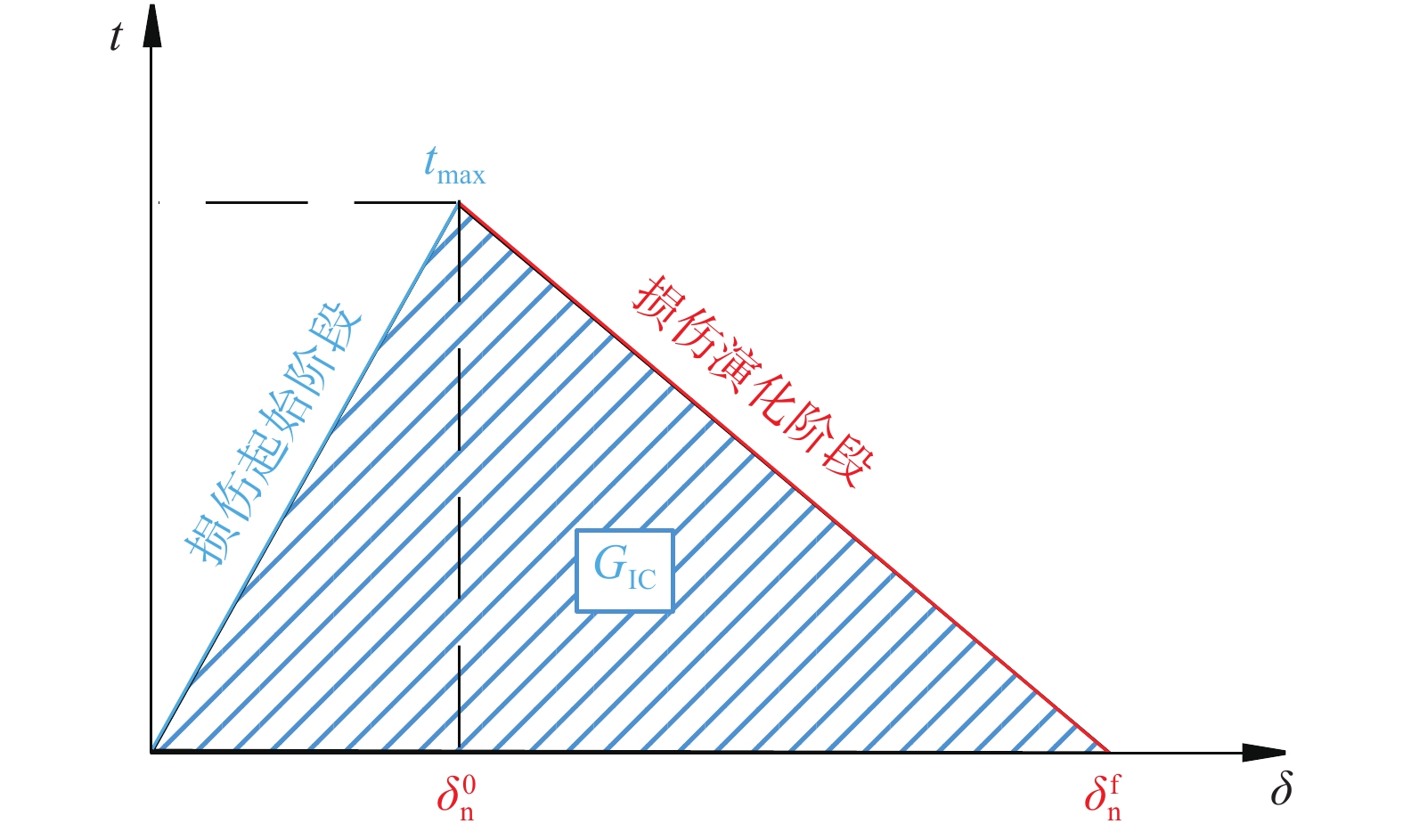
在锚杆拉拔过程中，锚固体的破坏失效往往存在裂纹扩展断裂过程区域，该区域可视为岩体在牵引力作用下产生的损伤区域。黏聚力单元是基于力-分离关系生成的1种单元，能够反映单元之间的分离失效形式，考虑这一种导致断裂的特性，能够在有限元模拟中比较真实的反映实体单元之间的黏结性能。为了很好地反映锚杆拉拔中岩石基体的开裂破坏，在前人基础上^[20]，使用黏聚力单元对岩石基体进行建模，黏聚力单元本构如图1，图中：t_max为损伤起始应力；$ {\delta }_{\text{n}}^{\text{0}} $为损伤起始位移；$ {\delta}_{\text{n}}^{\text{f}} $为损伤失效位移。

图  1  黏聚力单元本构

Figure  1.  Cohesive element constitutive

下载: 全尺寸图片 幻灯片

Cohesive单元牵引力-分离本构方程如式（1）：

式中：t_n、t_s、t_t分别为法向和2个剪切方向的名义应力；δ_n、δ_s、δ_t为法向和2个剪切方向的相对位移；k_nn、k_ss、k_tt分别为法向和2个剪切方向的弹性刚度；E为黏聚力单元刚度矩阵；δ为黏聚力单元位移矢量。

选用QUADS准则，表达式为：

式中：$ {{t}}_{\text{n}}^{\text{max}} $、$ {{t}}_{\mathrm{s}}^{\text{max}} $、$ {{t}}_{\mathrm{t}}^{\text{max}} $分别为3个方向的损伤应力，当应力比值的二次相互作用函数达到 1 时损伤开始演化。

2.   锚杆拉拔模型及模拟方法

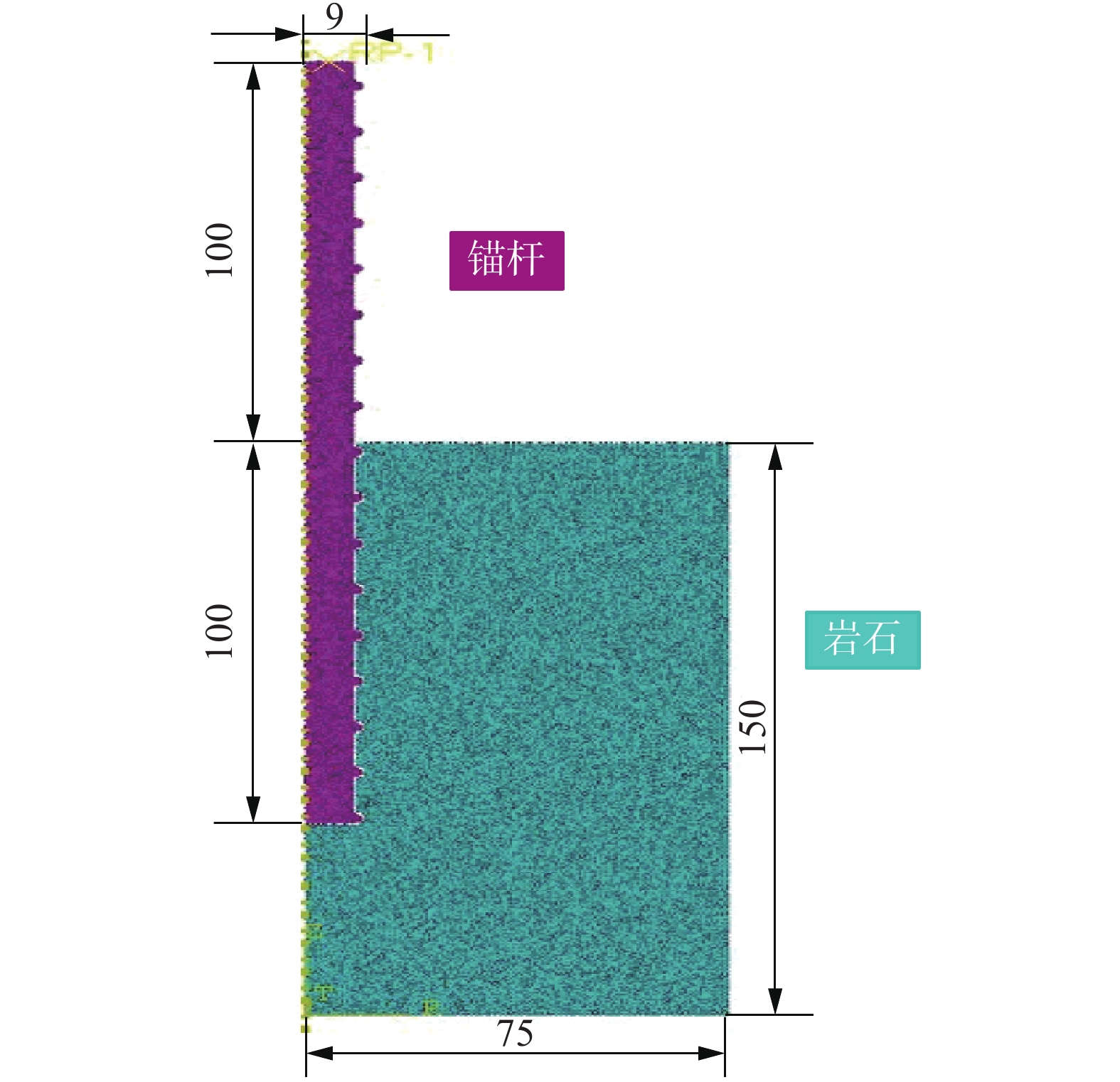
根据以往锚杆拉拔试验参数^[19]，采用ABAQUS有限元软件建立轴对称平面模型，螺纹钢锚杆模型杆体长度为200 mm，直径为18 mm，横肋间距分别为12、24、36、48 mm，肋底宽3 mm，肋高2 mm，锚固长度为100 mm，岩体模型尺寸为ϕ150 mm×150 mm。然后导入已经建好的锚杆和岩体模型，采用切割几何，截割得到不同锚杆横肋间距下的岩体模型，将锚杆和岩体进行装配，组合成1个锚固模型。锚固体轴对称模型如图2（肋间距12 mm）。

图  2  锚固体轴对称模型

Figure  2.  Axisymmetric model of anchored body

下载: 全尺寸图片 幻灯片

为了更真实的模拟锚杆拔出岩体的裂缝起裂和扩展，在划分后的模型中插入0厚度的cohesive单元。实体模型均采用CAX4R 四结点双线性轴对称四边形单元，cohesive单元为COHAX4四结点轴对称黏结单元，模型网格单元数为41 421。模型下边界施加x、y、z 3个方向位移及转角约束，右边界限制x方向位移，锚杆顶端施加位移荷载。

模型建立完成之后，根据煤矿岩石力学参数和煤矿所用锚杆材料参数，定义锚杆岩体模型的材料力学属性以及锚杆与岩体的接触方式。采用延性金属损伤模型描述锚杆的损伤行为，采用Drucker-Prager 准则描述岩石破坏行为及强度特性，材料力学参数见表1。岩体和锚杆之间的相互作用设置为符合线性损伤演化规律的黏聚接触模型，力学参数为：①刚度系数k_nn、k_ss、k_tt分别为100、100、100 MPa/mm；②损伤强度$ t_{\text{n}}^0 $、$t_{\text{s}}^0 $、$ t_{\text{t}}^0 $分别为4、4、4 MPa；③破坏位移为0.5 mm。

表  1  材料力学参数

Table  1.  Mechanical parameters of materials

名称	密度/(kg·m−3)	弹性模量/GPa	泊松比	内摩擦角/(°)	黏聚力/MPa
锚杆	7 850	210	0.3	-	-
岩体	2 800	30	0.2	36	13

下载: 导出CSV 

| 显示表格

3.   数值模拟结果

3.1   锚固极限承载力及拉拔破坏失效形式

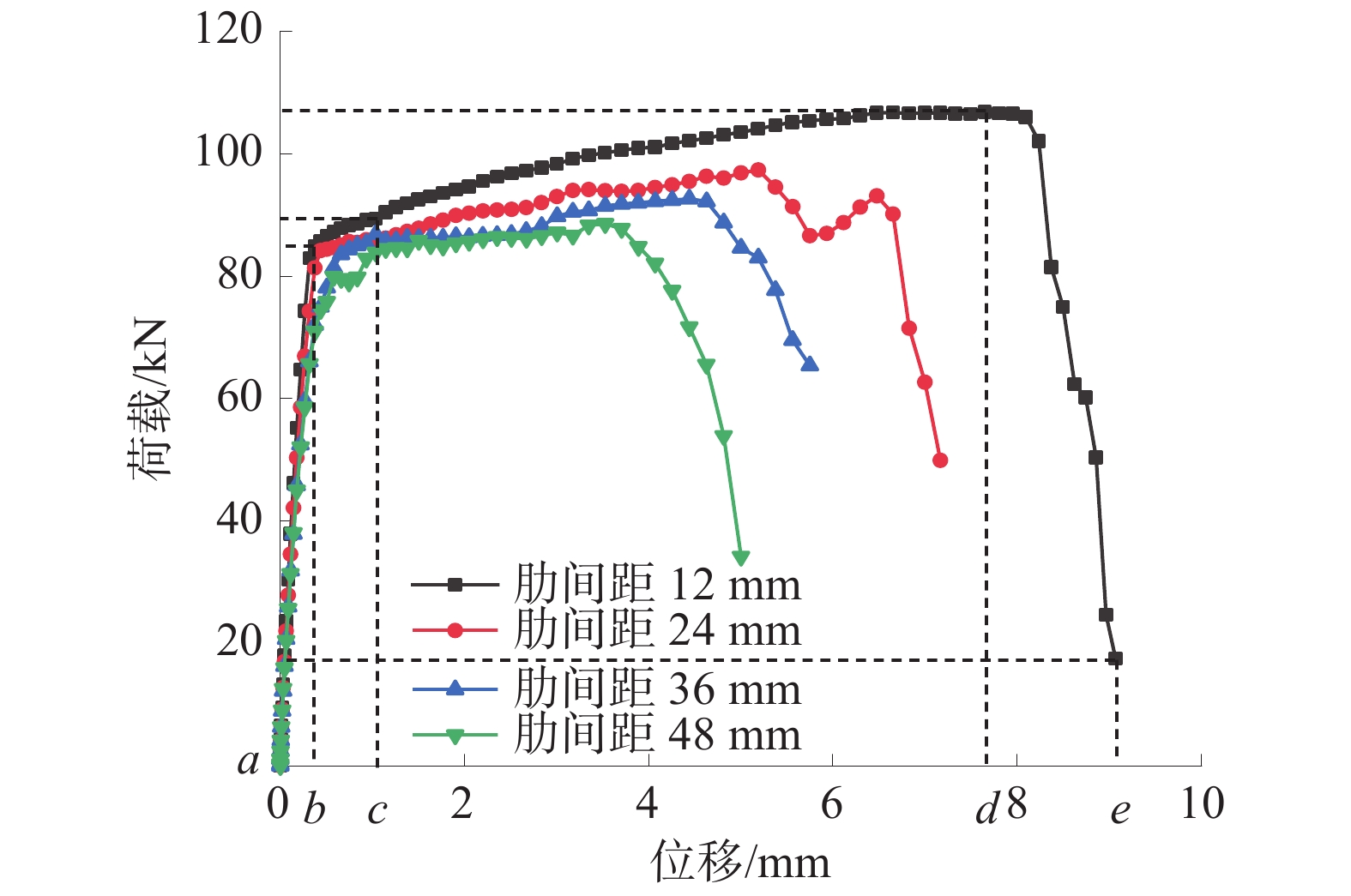
由数值模拟得到的不同肋间距锚杆的拉拔荷载-位移曲线如图3。

图  3  不同肋间距锚杆拉拔荷载-位移曲线

Figure  3.  Pull-out load-displacement curves of bolts with different rib spacing

下载: 全尺寸图片 幻灯片

在轴向荷载作用下，锚固体失效过程大体上依次经历初始弹性-短暂硬化-硬化-软化4个阶段。以肋间距12 mm拉拔荷载-位移曲线为例，图3中：a点为拉拔位移起始点；b点拉拔位移为 0.37 mm；c点拉拔位移为 1.25 mm；d点拉拔位移为 7.64 mm；e点拉拔位移为 9.06 mm。在拉拔过程中依次经历：①初始弹性阶段(a-b)：此时锚杆与岩体没有产生相对滑动;②短暂硬化阶段(b-c)：锚固界面出现塑性滑移变形；③硬化阶段(c-d)：锚固界面开始脱黏失效；④软化阶段(d-e)：锚固体完全开裂破坏。

由图3可知：不同锚杆弹性阶段和短暂硬化阶段的承载力差距较小；当锚杆进入硬化阶段后，随着锚杆肋间距的减小，锚杆硬化阶段也越长，即锚杆及锚固体能够允许的拉拔位移也越大；相比大肋间距的锚杆，小肋间距锚杆在经历了较大的变形后才会失效，同时，在相同的拉拔位移下，小肋间距锚杆也能够承受更高的拉拔荷载。

由图3可知：当锚杆肋间距分别为12、24、36、48 mm时，锚固极限承载力分别为106.83、97.35、92.68、88.58 kN；与肋间距48 mm相比，12、24、36 mm肋间距锚杆锚固极限承载力分别提高了20.69%、9.90%、4.62%；当肋间距达到12 mm时，相比24、36、48 mm的肋间距，锚固极限承载力提高显著。随着锚杆肋间距的减少，锚固极限承载力峰值增加，这表明小肋间距锚杆对巷道围岩变形的承载能力更强，而大肋间距锚杆更易失锚。

3.2   锚固体破坏过程

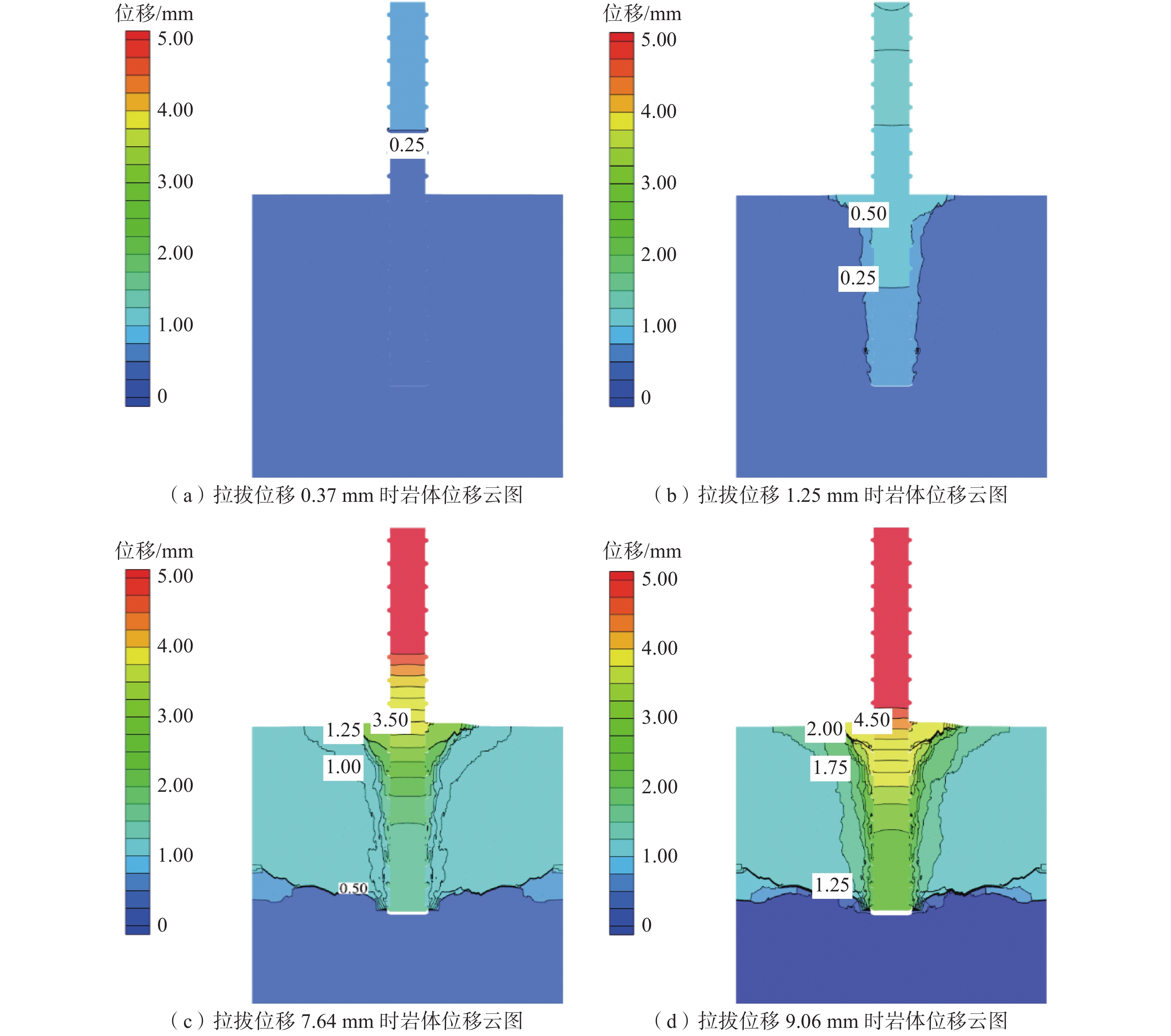
锚固体位移云图（肋间距12 mm）如图4。

图  4  锚杆拉拔锚固体位移场分布演化

Figure  4.  Evolution of displacement field distribution of bolt pull-out anchor body

下载: 全尺寸图片 幻灯片

由图4可知：位移加载到0.37 mm时，锚杆横肋与岩体接触位置开始变形，岩体的位移峰值为0.034 mm；当位移加载到1.25 mm时，岩体的位移峰值为0.32 mm，岩体在端头处开始产生裂纹；当位移加载到7.64 mm时，岩体的位移峰值为3.31 mm，岩体端头处呈倒碗状破坏；当位移加载到9.06 mm时，岩体的位移峰值为4.79 mm，锚固体裂隙扩展贯通；岩体的最大位移为4.79 mm，出现在锚固段端口处；岩体锚固段端口处位移明显高于其他区域，表明岩体出现破裂和离层。随着拉拔位移的增加，岩体破坏和离层区域呈倒碗形向岩体深部扩散；当拉拔位移增加至9.06 mm后，岩体锚固段末端处位移增速加大，最终导致锚固段基体破坏。

3.3   锚杆轴向应力

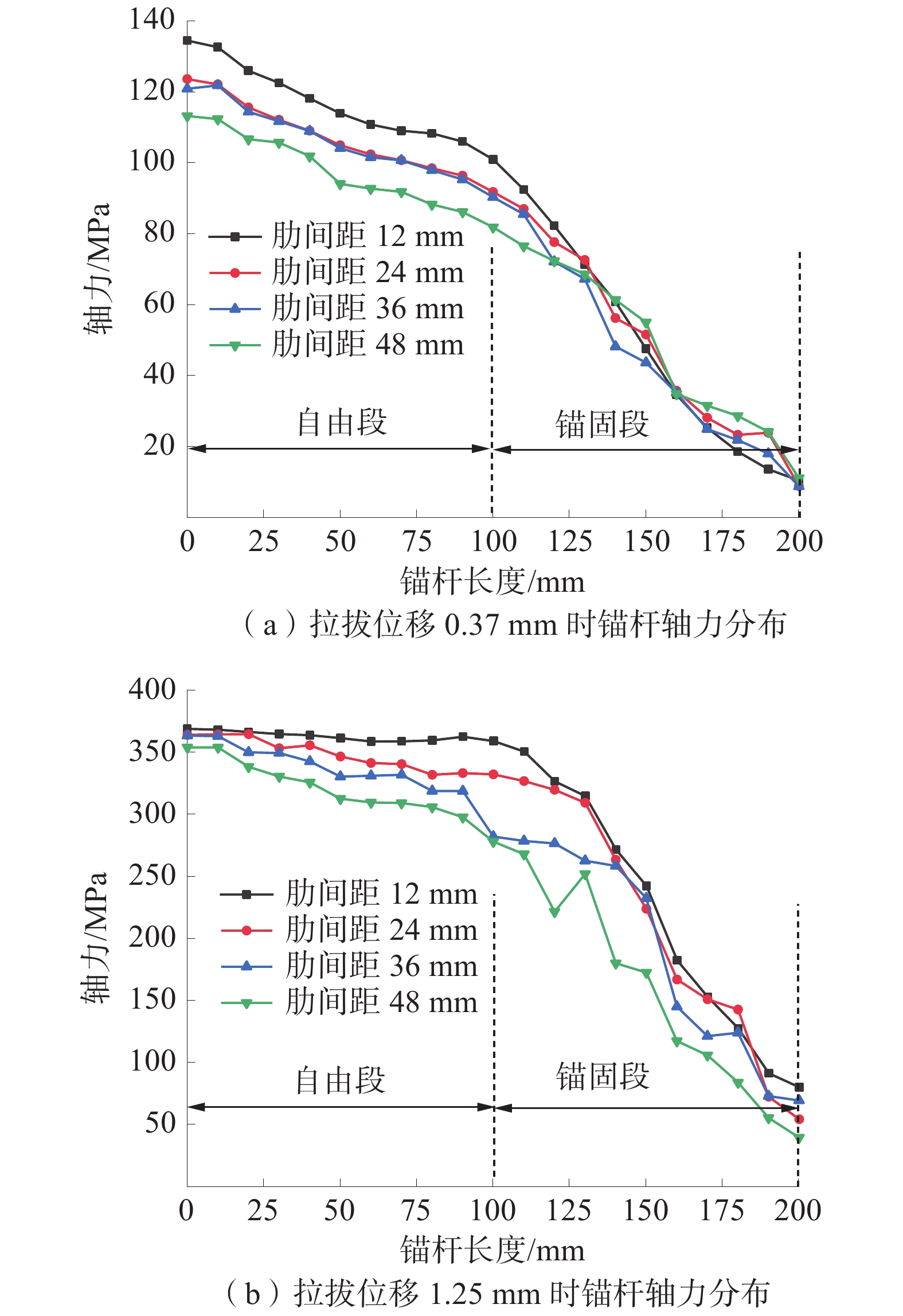
沿锚杆长度，每隔10 mm布置1个测点，获得的肋间距12、24、36、48 mm锚杆轴力沿锚杆长度的分布曲线如图5。

图  5  锚杆轴力分布曲线

Figure  5.  Axial force distribution curves of bolt

下载: 全尺寸图片 幻灯片

由图5可知：不同肋间距锚杆轴力分布规律较为一致，锚杆自由段轴力大于锚固段；在锚杆拉拔初期（拉拔位移0.37 mm时），锚杆轴力在锚固段差别不大，而在自由端具有较大区别；而随着锚杆拉拔位移的增加（拉拔位移1.25 mm时），锚杆锚固段轴力出现明显差距，而锚杆自由段，尤其是锚杆尾部轴力趋于一致；随着肋间距的增加，锚杆自由段轴力也有所增加；相比其他锚杆，12 mm肋间距锚杆自由段轴力变化较小，自由端轴力分布也更加均匀，锚杆受力条件也更好。

由锚杆轴力分布曲线得出，锚杆轴力与锚杆肋间距呈负相关，锚杆的轴力随着肋间距的减小而增加。

4.   结　语

1）根据数值模拟荷载-位移曲线得出，锚固体极限承载力与锚杆肋间距呈负相关,在相同的拉拔位移下，小肋间距锚杆也能够承受更高的拉拔荷载。横肋的存在提高了锚杆与岩体之间接触面积，提高了锚固界面的摩擦力和增强了机械互锁作用。

2）锚固体破坏失效过程为首先在锚固段端头处出现应力集中，当应力超过岩体强度时，岩体开始破坏。随着拉拔位移的施加，端头处呈倒碗状破坏，破坏范围向锚杆段深部扩展延伸，最后，锚固段基体破坏。

3）不同肋间距锚杆轴力分布是不均匀的，但其分布规律基本一致，锚杆轴力与锚杆肋间距呈负相关，锚杆的轴力随着肋间距的减小而增加。