Study on dynamic evolution law of development height of overburden water-flowing fractured zone
-
摘要:
为了研究覆岩导水裂隙带发育高度动态演化规律，以小保当矿区2−2煤层为研究对象，通过理论分析、相似模拟实验及实例验证的方法，对导水裂隙带动态发育高度进行研究；借助概率积分法预计其上部岩层移动变形的理论公式，给出了1种基于覆岩曲率变形的导水裂隙带动态发育高度预计方法。研究表明：导水裂隙带上部岩层下沉系数是1个与挠度及下部自由空间高度相关的分段函数，上部岩层曲率变形大小是决定导水裂隙带发育高度的关键因素；导水裂隙带发育高度与工作面推进长度相关；理论预计小保当矿区2−2煤层导水裂隙带发育高度为160.8 m，相似模拟实验发育高度为155 m，现场实测发育高度为152.01~175.57 m。
Abstract:In order to study the dynamic evolution law of the development height of overburden water conducting fractured zone, taking 2−2 coal seam in Xiaobaodang Mining Area as the research object, the dynamic development height of water conducting fractured zone was studied by theoretical analysis, similar simulation experiment and case verification; a prediction method of dynamic development height of water-flowing fractured zone based on curvature deformation of overburden strata is proposed by using the theoretical formula of predicting the movement and deformation of upper strata with probability integral method. The research shows that the subsidence coefficient of the upper strata of the water-conducting fractured zone is a piecewise function related to the deflection and the height of the lower free space. The curvature deformation of the upper strata is the key factor to determine the development height of the water-conducting fractured zone. The development height of water-flowing fractured zone is related to the advance length of working face; the theoretical prediction of the development height of the water conducting fractured zone in 2−2 coal seam of Xiaobaodang Mining Area is 160.8 m, the development height of the similar simulation experiment is 155 m, and the development height of the field measurement is 152.01-175.57 m.
-
采动诱发覆岩裂隙贯穿覆岩隔水层，极易造成生态水资源破坏和矿井水害，对生态环境的破坏尤为明显。钱鸣高[1]提出了煤矿绿色开采的理念，认为保水开采是绿色开采中的一项重要内容。目前相关学者对导水裂隙带发育规律进行了大量的研究，提出了隔水层隔水性不受破坏是保水开采的关键[2-5]，揭示了煤层赋存条件、开采方法、开采参数及关键层位置对导水裂隙带发育高度的影响[6-18]，通过理论分析、数学软件模拟及对大量实测数据的分析，总结了多种导水裂隙带发育高度理论预计方法，构建了导水裂隙带发育高度预测模型[15-21]。覆岩导水裂隙带发育高度与覆岩移动变形息息相关，虽然前人已对导水裂隙带发育高度进行了大量研究，但将覆岩移动变形与覆岩导水裂隙带发育高度有机结合方面研究相对较少。为此，基于前人研究成果，以小保当矿区2−2号煤层为研究对象，通过理论分析、相似模拟实验和实例验证的方法研究导水裂隙带动态发育高度，借助概率积分法预计导水裂隙带上部岩层的曲率变形，给出1种导水裂隙带动态发育高度的理论预计方法，为进一步分析采动过程中导水裂隙带发育高度动态演化规律和预计导水裂隙带发育高度提供理论依据。
1. 导水裂隙带发育高度动态演化理论
1.1 导水裂隙带发育高度与曲率变形的关系
采动诱发的覆岩移动破坏具有明显分带性，根据移动破坏特征将覆岩分为“三带”，其中垮落带和裂隙带共同组成导水裂隙带，导水裂隙带上部至地表范围内的岩层为弯曲下沉带。导水裂隙带上部岩层作为导水裂隙带与弯曲下沉带分界岩层，其是否破断对导水裂隙带发育高度有重要影响，因此对导水裂隙带发育高度的研究以分析导水裂隙带上部岩层变形破坏为主。
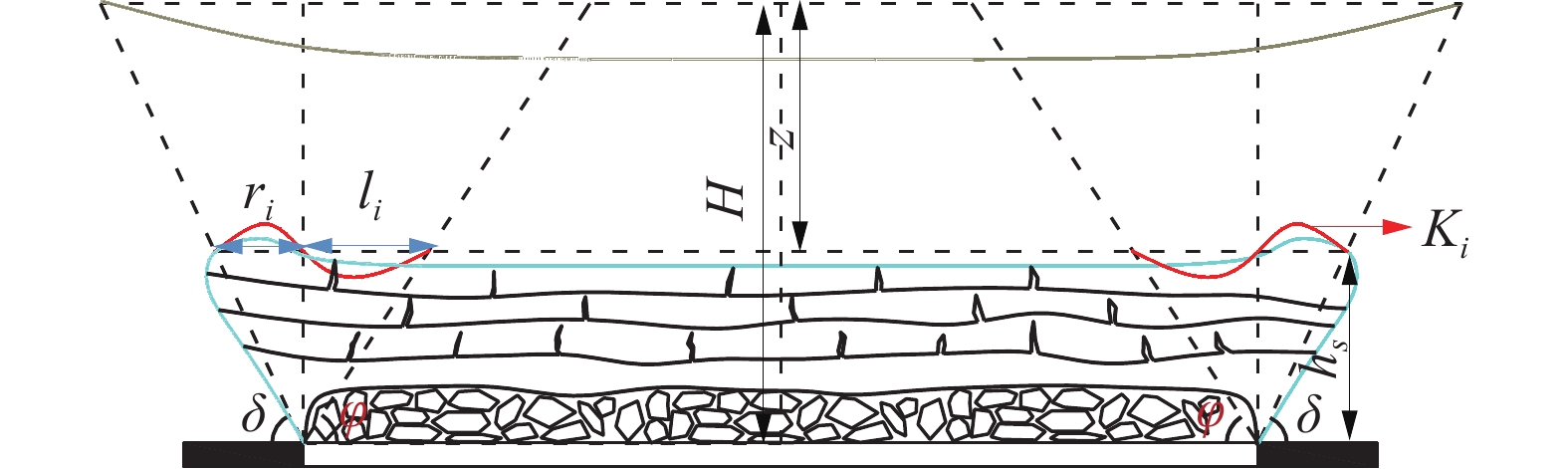
采动后覆岩发生弯曲，其弯曲程度随工作面推进长度增大逐渐加剧，当导水裂隙带上部岩层弯曲程度超过自身极限时，裂缝沿其法线方向向上发育，发育高度取决于导水裂隙带上部岩层曲率变形Ki大小[22]。地表与导水裂隙带上部岩层分别为弯曲下沉带上部与下部边界，其移动变形属于同一问题的2方面，移动变形规律相似，采用概率积分法可对导水裂隙带上部岩层移动变形进行分析[23]。导水裂隙带发育高度形态如图1。
![]()
图 1 导水裂隙带发育高度示意图Figure 1. Development height diagram of water conducting fractured zone图1中：hs为导水裂隙带发育高度，m；δ为移动角，（°）；φ为采动角，（°）；Ki为导水裂隙带上部岩层曲率变形，10−3/m；H为开采煤层埋藏深度，m；z为导水裂隙带上部岩层埋深，m；ri为导水裂隙带上部岩层主要影响半径，m；li为导水裂隙带上部岩层平底点距开采边界距离，m。
导水裂隙带上部岩层各点曲率变形值Ki表达式为：
$$ {K_i} = - 2{\text{π }}\frac{{{\eta _i}m\;\cos\; \alpha }}{{r_i^3}}x{{\mathrm{e}}^{ - {\text{π }}\frac{{{x^2}}}{{r_i^2}}}} $$ (1) 式中：ηi为导水裂隙带上部岩层下沉系数；m为煤层开采高度，m；α为煤层倾角，（°）；x为导水裂隙带上部岩层任一点位置。
煤层开采后覆岩发生破断，破断岩层在采空区发生堆积，由于岩石具有碎胀性，导水裂隙带上部岩层下沉值一般小于煤层开采高度m，其下沉系数ηi表达式为：
$$ {\eta _i} = \frac{{{w_i}}}{{m\;\cos \;\alpha }} $$ (2) 式中：wi为导水裂隙带上部岩层下沉值，m。
导水裂隙带上部岩层最大曲率变形值相应点位置x的表达式为：
$$ x = \frac{{{r_i}}}{{\sqrt {2{\text{π }}} }} = 0.4{r_i} $$ (3) 将式（3）代入式（1）中，可得导水裂隙带上部岩层最大曲率变形值Kimax表达式为：
$$ {K_{i\max }} = \pm 1.52\frac{{{\eta _i}m\;\cos\; \alpha }}{{r_i^2}} $$ (4) 采动诱发覆岩移动破坏是1个随工作面推进长度改变动态变化的过程，工作面推进长度增大，覆岩破坏发育高度、导水裂隙带上部岩层层位及曲率变形均发生变化，分析采动过程中覆岩动态破断规律，确定导水裂隙带上部岩层层位及曲率变形大小是预计导水裂隙带动态发育高度的关键。
1.2 采动覆岩动态破断规律
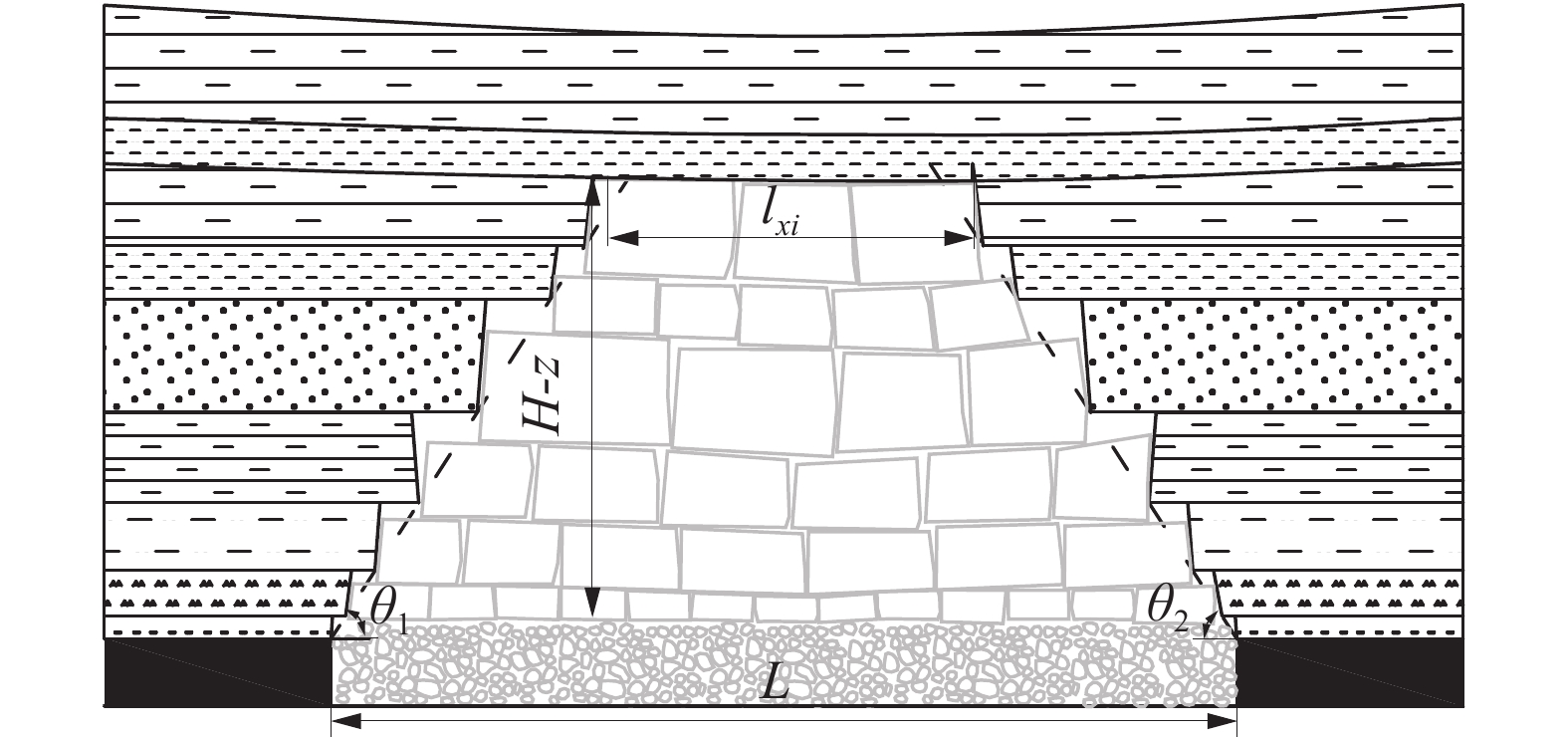
煤层采出后采空区上覆岩层失去支撑出现悬露，悬露长度lxi随工作面推进长度L增大而增大，工作面推进长度L与岩层悬露长度lxi的关系如图2。
图2中：lxi为岩层悬露长度，m；θ1、θ2分别为开切眼与工作面侧覆岩破断角，（°）；L为工作面推进长度，m。由图2可知，工作面推进长度L与岩层悬露长度lxi存在如下关系：
$$ {l_{xi}} = L - \left( {H - z} \right)\left( {\cot \;{\theta _1} + \cot \;{\theta _2}} \right) $$ (5) 由式（5）可知：当岩层埋深一定时，工作面推进长度L越长，第i层岩层悬露长度lxi越大；当第i层岩层破断时悬露长度为其破断距lpi，此时工作面推进长度为第i层岩层破断时的推进长度Lpi。
由于破断岩层具有碎胀性，第i层岩层下部自由空间高度∆i随破断岩体垮落堆积逐渐减小，当下部自由空间高度∆i小于第i层岩层挠度fimax时，下部自由空间高度∆i不足以诱发第i层岩层破断，覆岩破断到一定高度后停止，此后即使工作面推进长度进一步增大至L≥Lpi时，第i层岩层及其上覆岩层不再发生破断[24]。第i层岩层下部自由空间高度∆i关系式为：
$$ {\Delta _i} = m - \left( {H - z} \right)\left( {{k_{\mathrm{c}}} - 1} \right)\;\cos\; \alpha $$ (6) 式中：∆i为下部自由空间高度，m；kc为岩石残余碎胀系数。
综上所述，结合工作面推进长度L、挠度fimax以及下部自由空间高度∆i给出1种采动中覆岩破断的判据，覆岩动态破断判据见表1。
表 1 覆岩动态破断判据Table 1. Dynamic fracture criterion of overburden rock推进长度/m 第i层岩层挠度/m 是否破断 L<Lpi fimax≥∆i 否 fimax<∆i 否 L≥Lpi fimax≥∆i 否 fimax<∆i 是 根据表1判断覆岩各岩层破断情况，可对采动中导水裂隙带上部岩层层位进行确定。若第i层岩层不破断，导水裂隙带于第i层岩层下部停止发育，第i层岩层为导水裂隙带上部岩层；反之则转入对第i+1层岩层破断情况进行判断。
1.3 导水裂隙带上部岩层下沉系数
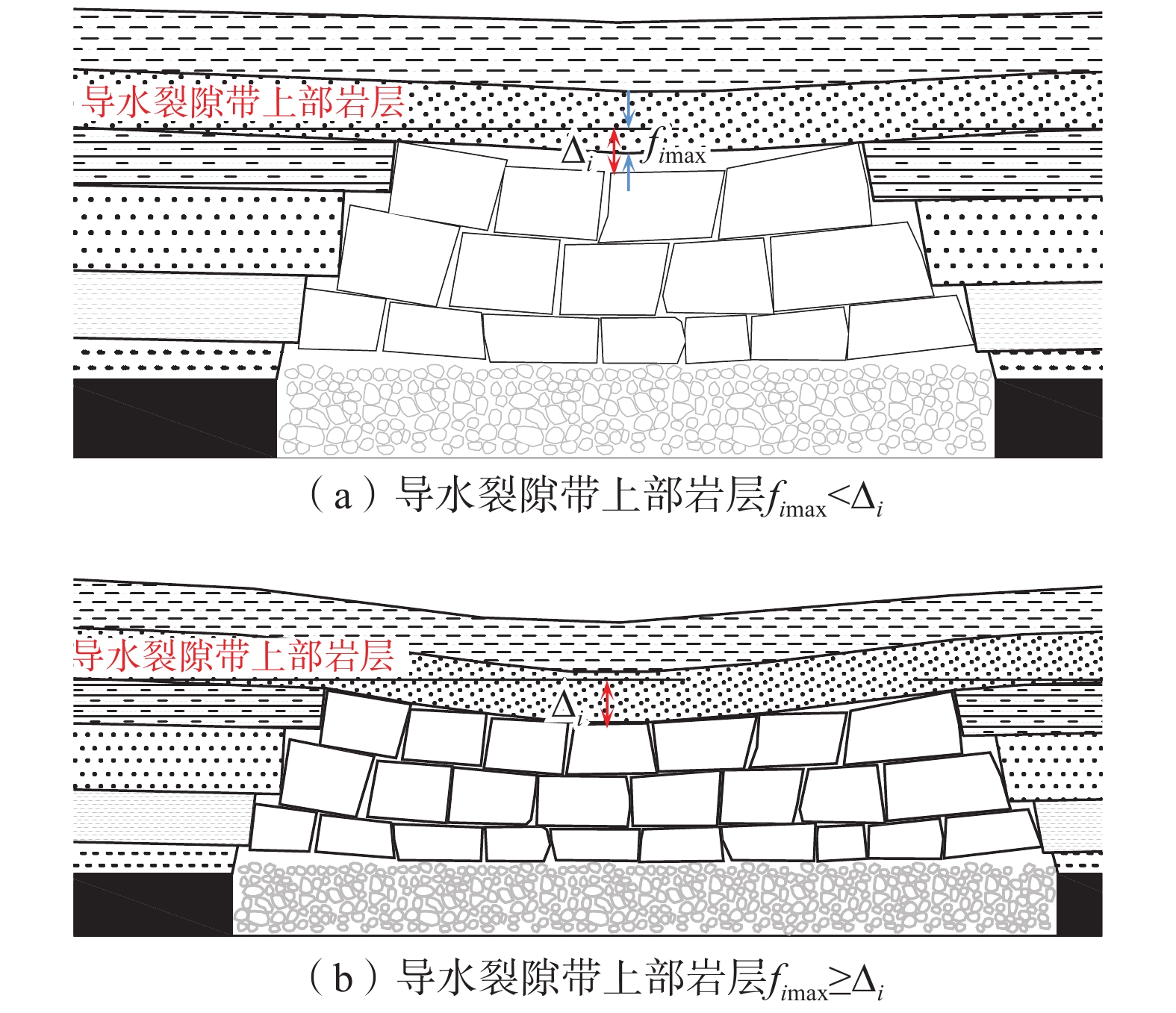
同一煤层上覆不同层位岩层物理力学性质不同，各岩层性质及厚度存在明显差异，因此采动中相邻岩层会出现不均匀下沉现象。覆岩不均匀下沉示意图如图3。
由图3可知，当覆岩出现不均匀下沉时，若导水裂隙带上部岩层挠度小于下部自由空间高度即fimax<∆i，其下沉值为挠度fimax；若导水裂隙带上部岩层挠度不小于下部自由空间高度即fimax≥∆i，导水裂隙带上部岩层与下方岩层接触，其下沉值为下部自由空间高度∆i。综上所述，采动中导水裂隙带上部岩层下沉系数ηi是1个与其下部自由空间∆i及挠度fimax有关的分段函数，表达式为：
$$ \left\{ \begin{gathered} {\eta _i} = \frac{{{\Delta _i}}}{m}\left( {{f_{i\max }} \geqslant {\Delta _i}} \right) \\ {\eta _i} = \frac{{{f_{i\max }}}}{m}\left( {{f_{i\max }} < {\Delta _i}} \right) \\ \end{gathered} \right. $$ (7) 导水裂隙带上部岩层下沉系数与其曲率变形值直接相关，基于概率积分法，结合导水裂隙带上部岩层下沉系数分段函数分析，可得导水裂隙带上部岩层曲率变形值。
1.4 导水裂隙带动态发育高度
苏联学者Б·я·гвельцман[22]通过实测数据得出全部垮落法开采导水裂隙带发育高度hs与导水裂隙带上部岩层极限曲率Kt存在如下关系表达式：
$$ h_{\mathrm{s}}^2 = \frac{{7.25{\eta _i}m}}{{{K_{\mathrm{t}}}{{\left( {\cot \;\delta + \cot\; \varphi } \right)}^2}}} $$ (8) 式中：Kt为导水裂隙带上部岩层极限曲率，10−3/m。
由图1可知，覆岩采动角φ与移动角δ反切值表达式为：
$$ \cot \;\delta = \frac{{{r_i}}}{{\left( {H - z} \right)}} $$ (9) $$ \cot \;\varphi = \frac{{{l_i}}}{{\left( {H - z} \right)}} $$ (10) 采动后裂缝沿弯曲岩层法线方向向上发育，发育高度取决于导水裂隙带上部岩层曲率变形的大小，将式（4）、式（9）、式（10）代入式（8）中即可得到基于导水裂隙带上部岩层曲率变形的导水裂隙带发育高度预计公式：
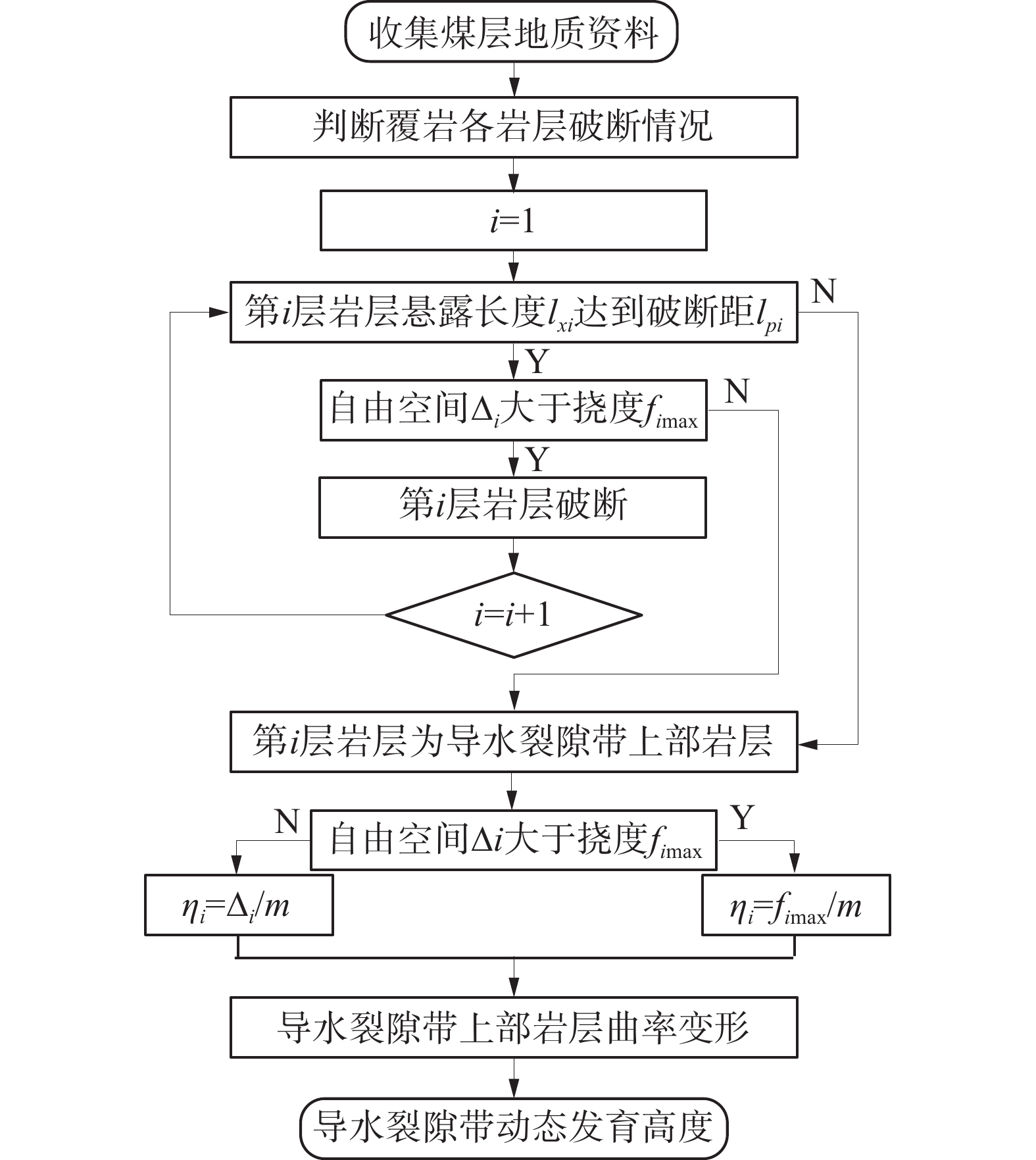
$$ h_{\mathrm{s}}^2 = \frac{{4.77{{\left( {H - z} \right)}^2}r_i^2{K_{i\;\max }}}}{{{K_{\mathrm{t}}}{{\left( {{r_i} + {l_i}} \right)}^2}\;\cos\; \alpha }} $$ (11) 导水裂隙带动态发育高度预计流程如图4。
![]()
图 4 导水裂隙带动态发育高度预计流程图Figure 4. Prediction flow chart of dynamic development height of water conducting fractured zone结合煤层赋存条件，判断采动中覆岩各岩层破断情况，确定不同工作面推进长度下导水裂隙带上部岩层层位、下沉系数和曲率变形，分析计算导水裂隙带动态发育高度。
2. 导水裂隙带发育高度相似模拟
2.1 工程概况
小保当矿区2−2号煤层倾角为0°~1°，属于近水平煤层，平均埋深为369.41 m，上覆基岩厚度为294.54 m，松散层厚度为68.87 m，平均采高6 m。各岩层相似模拟配比见表2。
表 2 相似模拟实验配比表Table 2. Similar simulation experiment ratio table序号 岩性 厚度/m 相似材料配比 河砂 石膏 大白粉 32 粉沙 2.70 9 1 9 31 细沙 53.80 9 1 9 30 红土 12.37 — — — 29 细粒砂岩 17.64 8 2 8 28 细粒砂岩 17.00 8 2 8 27 泥岩 7.00 9 2 8 26 细粒砂岩 2.20 8 2 8 25 砂质泥岩 7.77 9 4 6 24 细粒砂岩 18.96 8 3 7 23 砂质泥岩 8.68 9 4 6 22 细粒砂岩 3.09 8 2 8 21 砂质泥岩 12.10 9 4 6 20 砂质泥岩 12.00 9 4 6 19 细粒砂岩 5.00 8 2 8 18 砂质泥岩 6.48 9 4 6 17 细粒砂岩 13.64 8 2 8 16 粉砂岩 16.70 7 2 8 15 细粒砂岩 10.10 8 3 7 14 粉砂岩 6.01 7 2 8 13 细粒砂岩 13.01 8 3 7 12 粉砂岩 15.13 7 2 8 11 细粒砂岩 8.66 8 3 7 10 粉砂岩 19.40 7 2 8 9 细粒砂岩 9.88 8 3 7 8 粉砂岩 8.20 7 2 8 7 细粒砂岩 14.90 8 3 7 6 煤（1−1） 2.00 粉煤灰∶河砂∶石膏∶大白粉= 21∶1∶2∶21 5 细粒砂岩 18.75 8 3 7 4 粉砂岩 4.20 7 2 8 3 细粒砂岩 5.10 8 3 7 2 中粒砂岩 8.34 8 2 8 1 细粒砂岩 3.50 8 3 7 煤（2−2） 6.00 粉煤灰∶河砂∶石膏∶大白粉= 21∶1∶2∶21 根据2−2号煤层赋存条件选取几何相似常数αi=200、密度相似常数αρ=1.56、应力相似常数ασ=αiαρ=312，搭建尺寸为3 000 mm×1 700 mm×200 mm的相似模型。
2.2 相似模拟结果
为减小边界效应，开切眼开掘位置距模型左边界40 cm（80 m），由开切眼处开始向右侧模拟开挖煤层，在距模型边界40 cm（80 m）处停止开采，煤层开采过程中采用PENTAXR-322NX型光学全站仪对模型测线进行观测。工作面推进不同距离时导水裂隙带发育高度如图5~图7。
![]()
图 5 工作面推进至119 m时导水裂隙带发育高度Figure 5. Development height of water conducting fractured zone with working face advancing 119 m![]()
图 6 工作面推进至278 m时导水裂隙带发育高度Figure 6. Development height of water conducting fractured zone with working face advancing 278 m![]()
图 7 工作面推进至428 m时导水裂隙带发育高度Figure 7. Development height of water conducting fractured zone with working face advancing 428 m由图5可知：当工作面推进至119 m时，覆岩10号岩层未发生破断，为工作面推进至119 m时导水裂隙带上部岩层，导水裂隙带发育至10号岩层下部，发育高度为63.6 m，为2−2号煤层采高（6 m）的10.6倍。
由图6可知：当工作面推进至278 m时，覆岩破坏发育高度随工作面推进而增大，导水裂隙带发育至16号岩层中部，16号岩层未破断，为工作面推进至278 m时导水裂隙带上部岩层，导水裂隙带发育高度155 m，为采高的25.8倍。
由图7可知：当工作面推进至428 m时开采完毕，覆岩垮落稳定后煤层开采达到充分采动，受下部自由空间高度限制，覆岩破坏发育高度不再随工作面推进而增大，导水裂隙带在16号岩层中部停止发育，发育高度不再随工作面推进而发生明显变化，覆岩16号岩层为导水裂隙带上部岩层，导水裂隙带最大发育高度155 m，为采高的25.8倍。
3. 导水裂隙带发育高度动态演化验证
3.1 导水裂隙带动态发育高度理论预计
根据覆岩破断判据，结合相似模拟实验现象及观测数据对采动过程中各岩层破断情况进行判定，覆岩破断情况判别表见表3。
表 3 覆岩破断情况判别表Table 3. Overburden rock fracture discrimination table岩层序号 岩层厚度/m Lpi/m ∆i/m 是否破断 16 16.70 212.0 4.52 否 15 10.10 212.0 4.63 是 14 6.01 168.0 4.69 是 13 13.01 168.0 4.82 是 12 15.13 155.0 4.97 是 11 8.66 126.0 5.06 是 10 19.40 126.0 5.25 是 9 9.88 119.0 5.35 是 8 8.20 99.0 5.43 是 7 14.90 99.0 5.58 是 6 2.00 99.0 5.60 是 5 18.75 90.0 5.79 是 4 4.20 76.0 5.83 是 3 5.10 76.0 5.88 是 2 8.34 53.0 5.97 是 1 3.50 41.6 6.00 是 由表3可知：当工作面推进至41.6 m时，煤层顶板发生破断，覆岩破坏开始向上发育；当推进长度达到53.0 m覆岩2号岩层发生破断，随着工作面推进长度增大，导水裂隙带逐步向上发育；在推进长度达到76.0 m时上覆3、4号岩层均发生破断，导水裂隙带发育至5号岩层下部；当推进至90.0 m时5号岩层发生破断，导水裂隙带进一步发育，其上覆6号~8号岩层在推进长度达到99.0 m时均发生破断；推进长度达到119 m时9号岩层破断，导水裂隙带发育至10号岩层下部；当推进至126.0 m时10号岩层与11号岩层发生同步破断，推进至155.0 m时12号岩层破断，导水裂隙带随覆岩破断向上发育；当推进长度达到168.0 m时13号、14号岩层同步破断，推进至212.0 m时覆岩15号岩层发生破断，由于f16max=6.61 m>∆16，16号岩层不破断，导水裂隙带于16号岩层下部停止发育，此后随着工作面推进长度增大，导水裂隙带发育高度不再发生明显变化。
为了进一步分析采动过程中的导水裂隙带动态发育高度，结合相似模拟实验现象及观测数据，以工作面推进长度119、278、428 m（在该推进长度下导水裂隙带上部岩层下沉系数分别对应其下沉系数的2个分段函数）为例预计2−2煤层开采过程中导水裂隙带发育高度，理论预计结果如下：
1）当工作面推进至119 m时10号岩层未破断，为导水裂隙带上部岩层。相似模拟实验观测得10号岩层l10=37.8 m，r10=38.2 m，下沉值w10=0.72 m，下沉系数η10=0.12，极限曲率Kt=1.30×10−3/m，推进至119 m时导水裂隙带上部岩层最大曲率变形值K10max=0.75×10−3/m，将上述数据代入式（11）中计算可得。工作面推进至119 m时导水裂隙带发育高度hs为62.4 m。
2）当工作面推进至278 m时，16号岩层未破断，为导水裂隙带上部岩层，相似模拟实验观测可得16号岩层l16=72.3 m，r16=72.9 m，下沉值w16=4.52 m，下沉系数η16=0.75，推进至278 m时导水裂隙带上部岩层最大曲率变形值K16max=1.29×10−3/m，将上述参数代入式（11）中计算可得工作面推进至278 m时导水裂隙带发育高度hs为160.8 m。
3）当工作面推进至428 m时，16号岩层仍未破断，下沉系数η16=0.75，曲率变形值K16 max=1.29×10−3/m，计算得当工作面推进至428 m时导水裂隙带发育高度仍为160.8 m，导水裂隙带发育高度不再随工作面推进长度增大发生明显变化，导水裂隙带最大发育高度hs为160.8 m。
3.2 相似模拟实验验证
当工作面推进至119 m时，相似模拟实验中导水裂隙带发育高度为63.6 m，理论预计结果为62.4 m，误差为1.9%；推进至278 m时，实验中导水裂隙带发育高度为155 m，理论预计结果为160.8 m，误差为3.6%；当2−2号煤层开采完成后，实验中导水裂隙带最大发育高度为155 m，理论预计导水裂隙带最大发育高度为160.8 m，误差为3.6%。
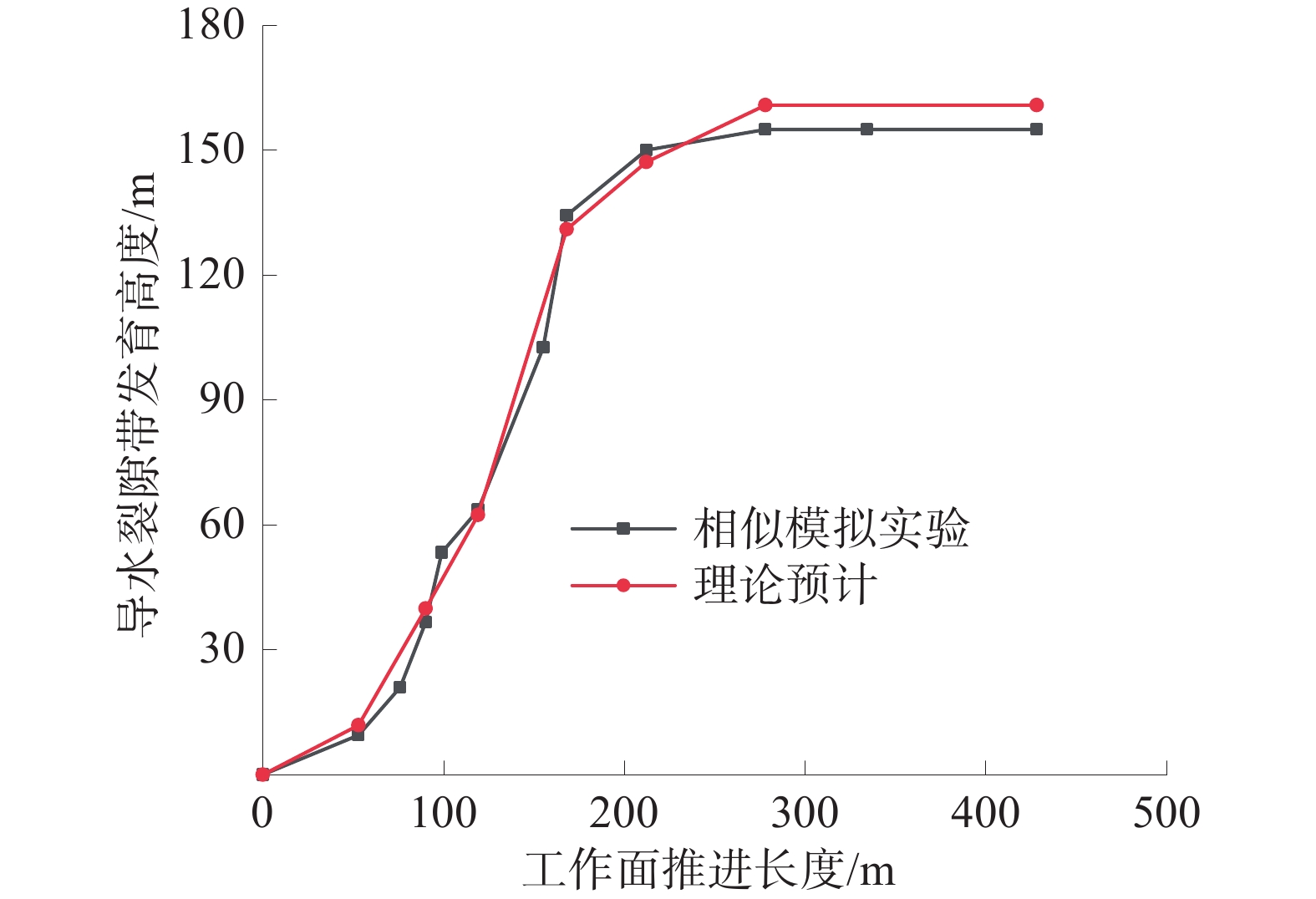
基于相似模拟实验及理论预计结果绘制的2−2煤层开采过程中导水裂隙带动态发育高度曲线图如图8。
![]()
图 8 覆岩导水裂隙带动态发育曲线Figure 8. Dynamic development curves of overburden water conducting fractured zone由图8可知，导水裂隙带发育高度理论预计曲线与相似模拟实验曲线基本一致，误差为1.9 %~3.6%，两段曲线均表明采动中导水裂隙带发育高度随工作面推进长度增大发生变化，其发育形态大致可分为以下4个阶段。
1）缓慢发育阶段。煤层开采初期，采空区尺寸相对较小，受采空区大小限制导水裂隙带发育相对缓慢。
2）迅速发育阶段。工作面进一步推进，覆岩受采动影响程度增大，导水裂隙带随工作面推进长度增大快速发育。
3）发育变缓阶段。导水裂隙带发育至一定高度后，采动对导水裂隙带上部岩层影响程度逐渐降低，此时导水裂隙带发育高度随工作面推进增速逐渐减缓。
4）发育平稳阶段。当工作面推进至一定长度后，由于岩石具有碎胀性，破断岩层将覆岩下部自由空间填满，导水裂隙带上部岩层不再发生破断，导水裂隙带达到最大发育高度，不再随工作面推进长度增大发生明显变化。
3.3 实例验证
小保当一号井2−2号煤层平均埋深356.5 m，上覆基岩厚度为202.65~288.89 m，平均254.14 m，松散层厚度为70.26 m，煤层平均厚度为5.8 m。为验证覆岩导水裂隙带发育高度预计理论的可靠性，以小保当一号井2−2号煤层为研究对象，对覆岩导水裂隙带发育高度进行了现场实测。
现场对6个钻孔进行探查，探查结果表明覆岩导水裂隙带发育高度为152.01~175.57 m，为采高的26.21~30.27倍，切眼附近导水裂隙带发育高度最大，工作面内部发育高度较小。理论预计小保当矿区2−2号煤层覆岩导水裂隙带最大发育高度为160.8 m，与现场实测覆岩导水裂隙带发育高度基本一致。
4. 结 语
1）基于工作面推进长度、挠度及下部自由空间高度给出了覆岩动态破断判据和导水裂隙带上部岩层下沉系数分段函数，在此基础上给出了1种基于导水裂隙带上部岩层曲率变形的导水裂隙带动态发育高度预计方法。
2）通过相似模拟实验和理论预计方法，揭示了采动中导水裂隙带发育高度动态演化的4个阶段：缓慢发育阶段、迅速发育阶段、发育变缓阶段、发育平稳阶段。
3）以小保当矿区2−2号煤层为研究对象对导水裂隙带发育高度进行理论预计、相似模拟实验及现场实测，理论预计结果与相似模拟实验结果误差为1.9 %~3.6%，理论预计发育高度为160.8 m，与现场实测2−2号煤层开采导水裂隙带发育高度152.01~175.57 m基本吻合。
-
![]()
图 1 导水裂隙带发育高度示意图
Figure 1. Development height diagram of water conducting fractured zone
![]()
图 4 导水裂隙带动态发育高度预计流程图
Figure 4. Prediction flow chart of dynamic development height of water conducting fractured zone
![]()
图 5 工作面推进至119 m时导水裂隙带发育高度
Figure 5. Development height of water conducting fractured zone with working face advancing 119 m
![]()
图 6 工作面推进至278 m时导水裂隙带发育高度
Figure 6. Development height of water conducting fractured zone with working face advancing 278 m
![]()
图 7 工作面推进至428 m时导水裂隙带发育高度
Figure 7. Development height of water conducting fractured zone with working face advancing 428 m
![]()
图 8 覆岩导水裂隙带动态发育曲线
Figure 8. Dynamic development curves of overburden water conducting fractured zone
表 1 覆岩动态破断判据
Table 1 Dynamic fracture criterion of overburden rock
推进长度/m 第i层岩层挠度/m 是否破断 L<Lpi fimax≥∆i 否 fimax<∆i 否 L≥Lpi fimax≥∆i 否 fimax<∆i 是 
下载: 导出CSV
表 2 相似模拟实验配比表
Table 2 Similar simulation experiment ratio table
序号 岩性 厚度/m 相似材料配比 河砂 石膏 大白粉 32 粉沙 2.70 9 1 9 31 细沙 53.80 9 1 9 30 红土 12.37 — — — 29 细粒砂岩 17.64 8 2 8 28 细粒砂岩 17.00 8 2 8 27 泥岩 7.00 9 2 8 26 细粒砂岩 2.20 8 2 8 25 砂质泥岩 7.77 9 4 6 24 细粒砂岩 18.96 8 3 7 23 砂质泥岩 8.68 9 4 6 22 细粒砂岩 3.09 8 2 8 21 砂质泥岩 12.10 9 4 6 20 砂质泥岩 12.00 9 4 6 19 细粒砂岩 5.00 8 2 8 18 砂质泥岩 6.48 9 4 6 17 细粒砂岩 13.64 8 2 8 16 粉砂岩 16.70 7 2 8 15 细粒砂岩 10.10 8 3 7 14 粉砂岩 6.01 7 2 8 13 细粒砂岩 13.01 8 3 7 12 粉砂岩 15.13 7 2 8 11 细粒砂岩 8.66 8 3 7 10 粉砂岩 19.40 7 2 8 9 细粒砂岩 9.88 8 3 7 8 粉砂岩 8.20 7 2 8 7 细粒砂岩 14.90 8 3 7 6 煤（1−1） 2.00 粉煤灰∶河砂∶石膏∶大白粉= 21∶1∶2∶21 5 细粒砂岩 18.75 8 3 7 4 粉砂岩 4.20 7 2 8 3 细粒砂岩 5.10 8 3 7 2 中粒砂岩 8.34 8 2 8 1 细粒砂岩 3.50 8 3 7 煤（2−2） 6.00 粉煤灰∶河砂∶石膏∶大白粉= 21∶1∶2∶21
下载: 导出CSV
表 3 覆岩破断情况判别表
Table 3 Overburden rock fracture discrimination table
岩层序号 岩层厚度/m Lpi/m ∆i/m 是否破断 16 16.70 212.0 4.52 否 15 10.10 212.0 4.63 是 14 6.01 168.0 4.69 是 13 13.01 168.0 4.82 是 12 15.13 155.0 4.97 是 11 8.66 126.0 5.06 是 10 19.40 126.0 5.25 是 9 9.88 119.0 5.35 是 8 8.20 99.0 5.43 是 7 14.90 99.0 5.58 是 6 2.00 99.0 5.60 是 5 18.75 90.0 5.79 是 4 4.20 76.0 5.83 是 3 5.10 76.0 5.88 是 2 8.34 53.0 5.97 是 1 3.50 41.6 6.00 是
下载: 导出CSV
-
[1] 钱鸣高. 煤炭的科学开采[J]. 煤炭学报,2010,35(4):529−534. QIAN Minggao. On sustainable coal mining in China[J]. Journal of China Coal Society, 2010, 35(4): 529−534.
[2] 王双明,黄庆享,范立民,等. 生态脆弱矿区含(隔)水层特征及保水开采分区研究[J]. 煤炭学报,2010,35(1):7−14. WANG Shuangming, HUANG Qingxiang, FAN Limin, et al. Study on overburden aquclude and water protection mining regionazation in the ecological fragile mining area[J]. Journal of China Coal Society, 2010, 35(1): 7−14.
[3] 黄庆享. 浅埋煤层保水开采隔水层稳定性的模拟研究[J]. 岩石力学与工程学报,2009,28(5):987−992. HUANG Qingxiang. Simulation of clay aquifuge stability of water conservation mining in shallow-buried coal seam[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(5): 987−992.
[4] 黄庆享. 浅埋煤层覆岩隔水性与保水开采分类[J]. 岩石力学与工程学报,2010,29(S2):3622-3627. HUANG Qingxiang. Impermeability of overburden rock in shallow buried coal seam and classification of water conservation mining[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 3622-3672.
[5] 孙学阳,卢明皎,李成,等. 双煤层错距开采优选及对隔水关键层影响研究[J]. 采矿与安全工程学报,2021,38(1):51−57. SUN Xueyang, LU Mingjiao, LI Cheng, et al. Optimal selection of staggered distance mining in double seams and its influence on water-resisting key strata[J]. Journal of Mining & Safety Engineering, 2021, 38(1): 51−57.
[6] 张京民,孟凡林,武海文,等. 烧变岩含水层下煤层开采导水断裂带发育规律研究[J]. 煤矿安全,2022,53(8):180−186. ZHANG Jingmin, MENG Fanlin, WU Haiwen, et al. Study on development law of water conducting fracture zone in coal seam mining under burnt rock aquifer[J]. Safety in Coal Mines, 2022, 53(8): 180−186.
[7] 刘瑞瑞,刘洋,方刚,等. 袁大滩煤矿覆岩破坏规律及顶板水害防治对策[J]. 煤矿安全,2022,53(7):82−91. LIU Ruirui, LIU Yang, FANG Gang, et al. Law of overburden failure and roof water damage in Yuandatan Coal Mine[J]. Safety in Coal Mines, 2022, 53(7): 82−91.
[8] 侯恩科,刘博,龙天文,等. 深埋缓倾斜双煤层开采导水断裂带发育规律研究[J]. 煤矿安全,2022,53(3):50−57. HOU Enke, LIU Bo, LONG Tianwen, et al. Study on development law of water-conducting fault zone in deep gently inclined double coal seam mining[J]. Safety in Coal Mines, 2022, 53(3): 50−57.
[9] 杨达明,郭文兵,赵高博,等. 厚松散层软弱覆岩下综放开采导水裂隙带发育高度[J]. 煤炭学报,2019,44(11):3308−3316. YANG Daming, GUO Wenbing, ZHAO Gaobo, et al. Height of water-conducting zone in longwall top-coal caving mining under thick alluvium and soft overburden[J]. Journal of China Coal Society, 2019, 44(11): 3308−3316.
[10] 李树刚,李志梁,林海飞,等. 采高对采动裂隙演化规律的影响研究[J]. 矿业安全与环保,2015,42(5):25−28. LI Shugang, LI Zhiliang, LIN Haifei, et al. Research on influence of mining height on mining fissure evolution[J]. Mining safety & Environmental Protection, 2015, 42(5): 25−28.
[11] 秦洪岩,王海东,张帆,等. 基于板壳理论的充填开采覆岩导水断裂带发育规律[J]. 煤矿安全,2021,52(1):64−70. QIN Hongyan, WANG Haidong, ZHANG Fan, et al. Development law of fractured zone of overburden strata in backfill mining based on plate and shell theory[J]. Safety in Coal Mines, 2021, 52(1): 64−70.
[12] 樊振丽,刘治国. 厚黏土层软弱覆岩采动破坏的泥盖效应[J]. 采矿与安全工程学报,2020,37(6):1196−1204. FAN Zhenli, LIU Zhiguo. Mud cover effect of mining-induced failure of soft overburden in thick clay strata[J]. Journal of Mining & Safety Engineering, 2020, 37(6): 1196−1204.
[13] 余学义,穆驰,李剑锋. 孟巴矿强含水体下分层开采覆岩导水裂隙带发育规律[J]. 煤炭学报,2022,47(S1):29−38. YU Xueyi, MU Chi, LI Jianfeng. Development law of water-conducting fracture zone in overlying rock with layered mining under strong water-bearing body in Barapukuria coal mine[J]. Journal of China Coal Society, 2022, 47(S1): 29−38.
[14] 赵宝峰. 上行开采条件下多煤层开采覆岩破坏规律研究[J]. 矿业安全与环保,2016,43(6):13−15. ZHAO Baofeng. Study on overlying strata failure rule in process of multi-seam ascending mining[J]. Mining safety & environmental protection, 2016, 43(6): 13−15.
[15] 尹尚先,徐斌,徐慧,等. 综采条件下煤层顶板导水裂隙带高度计算研究[J]. 煤炭科学技术,2013,41(9):138−142. YIN Shangxian, XU Bin, XU Hui, et al. Study on height calculation of water conducted fractured zone caused by fully mechanized mining[J]. Coal Science and Technology, 2013, 41(9): 138−142.
[16] 黄万朋,高延法,王波,等. 覆岩组合结构下导水裂隙带演化规律与发育高度分析[J]. 采矿与安全工程学报,2017,34(2):330−335. HUANG Wanpeng, GAO Yanfa, WANG Bo, et al. Evolution rule and development height of permeable fractured zone under combined-strata structure[J]. Journal of Mining & Safety Engineering, 2017, 34(2): 330−335.
[17] 许家林,王晓振,刘文涛,等. 覆岩主关键层位置对导水裂隙带高度的影响[J]. 岩石力学与工程学报,2009,28(2):380−385. XU Jialin, WANG Xiaozhen, LIU Wentao, et al. Effects of primary key stratum location on height of water flowing fracture zone[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(2): 380−385.
[18] 许家林,朱卫兵,王晓振. 基于关键层位置的导水裂隙带高度预计方法[J]. 煤炭学报,2012,37(5):762−769. XU Jialin, ZHU Weibin, WANG Xiaozhen. New method to predict the height of fractured water-conducting zone by location of key strata[J]. Journal of China Coal Society, 2012, 37(5): 762−769.
[19] 乔伟,韩昌民,李连刚,等. 煤矿导水裂隙带高度预测的PSO-SVR法及应用[J]. 煤炭科技,2022,43(4):77−84. QIAO Wei, HAN Changmin, LI Liangang, et al. PSO-SVR method for the height of water flowing fractured zone in coal mine and its application[J]. Coal Science & Technology Magazine, 2022, 43(4): 77−84.
[20] 赵兵朝,余学义. 导水裂隙带的广义损伤因子研究[J]. 中国矿业大学学报,2010,39(5):705−708. ZHAO Bingchao, YU Xueyi. Research on broad sense damage gene of fracture zone[J]. Journal of China University of Mining & Technology, 2010, 39(5): 705−708.
[21] 赵兵朝,刘樟荣,同超,等. 覆岩导水裂隙带高度与开采参数的关系研究[J]. 采矿与安全工程学报,2015,32(4):634−638. ZHAO Bingchao, LIU Zhangrong, TONG Chao, et al. Relation between height of water flowing fractured zone and mining parameters[J]. Journal of Mining & Safety Engineering, 2015, 32(4): 634−638.
[22] 格维尔茨曼. 水体下安全采煤[M]. 北京:煤炭工业出版社,1980:62-68. [23] 余学义,张恩强. 开采损害学[M]. 北京:煤炭工业出版社,2010:53-62. [24] 郭文兵,娄高中. 覆岩破坏充分采动程度定义及判别方法[J]. 煤炭学报,2019,44(3):755−766. GUO Wenbing, LOU Gaozhong. Definition and distinguishing method of critical mining degree of overburden failure[J]. Journal of China Coal Society, 2019, 44(3): 755−766.
-
期刊类型引用(7)
1. 范铭今，陈军涛，古海龙，唐道增，韩港，张树强，李光强. 西部矿区可注断层破碎带注浆加固特性试验研究. 煤矿安全. 2025(01): 155-163 . 
本站查看
2. 谢宇航，华心祝. 废弃矿井双煤层开采覆岩裂隙发育规律研究. 中国矿业. 2025(01): 137-145 . 百度学术
3. 夏玉成，孙学阳，苗霖田，郭晨，杜荣军. 智能时代的矿井地质工作展望——矿井开采智能地质保障技术体系架构. 煤田地质与勘探. 2025(01): 64-76 . 百度学术
4. 齐跃明，周沛，周来，蒋丹，杨雨晴，刘延卓. 考虑采动效应的闭坑矿井水硫酸盐污染规律. 煤田地质与勘探. 2024(04): 89-100 . 百度学术
5. 张瑾，段凯，马军伟. 回采工作面覆岩破断规律及导水裂隙发育高度研究. 价值工程. 2024(29): 82-85 . 百度学术
6. 段凯，苏建军. 中硬-坚硬互层覆岩导水裂隙带发育高度数值模拟及实测研究. 山西煤炭. 2024(04): 128-134 . 百度学术
7. 吴斌斌. 锦界煤矿31301工作面导水裂缝带发育高度研究. 中国煤炭. 2024(S1): 120-127 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 78
- HTML全文浏览量: 9
- PDF下载量: 27
- 被引次数: 11
