作为我国传统能源之一，煤炭始终占据一次性能源市场50%~60%以上的份额。随着煤矿开采深度的增加，煤矿安全事故呈多发态势，煤矿瓦斯事故又是煤矿安全生产最主要的灾害之一。煤矿瓦斯事故种类繁多（如瓦斯窒息、瓦斯爆炸及煤与瓦斯突出等）、破坏性强，严重危害了煤矿开采工作中人员和财产安全。矿井通风和瓦斯抽采等瓦斯治理技术的实施可以有效地将矿井瓦斯浓度控制在安全范围内，预防瓦斯事故的发生。而回采工作面瓦斯涌出量预测是矿井瓦斯治理工作的关键一环，如何能够对回采工作面瓦斯涌出量及其回风瓦斯体积分数进行科学、准确的预测，合理的预测方法的研究必不可少，对煤矿的安全生产具有重大意义。

国内外许多煤炭相关领域的专家学者针对瓦斯涌出量预测这一课题做出了大量研究，目前，分源预测法、矿山统计法、瓦斯地质数学模型法、灰色预测法、神经网络预测法及组合预测法等方法被广泛使用^[1-4]。其中，灰色预测以其所需数据量小、可忽略各因素对预测数据的具体影响模式而受到大量研究人员的青睐。肖鹏等^[5]考虑各影响因素的作用，建立了多变量灰色模型，使瓦斯涌出量的预测趋势更加合理；为了提高预测精度，秦志^[6]利用最近的3组数据进行动态预测；侯殿坤等^[7]用新信息取代无法准确反映系统特征的旧数据，效果显著。灰色预测模型持续拓展，越来越多将其与其他预测方法组合优化的新模型被提出。由于灰色预测难以适应波动较大的长期预测，高保彬等^[8]采用马尔科夫预测修正灰色预测结果；熊祖强等^[9]利用无偏灰色 GM( 1，1) 模型建立了动态无偏灰色马尔科夫模型；田水承等^[10]建立了一种等维新息无偏灰色马尔可夫预测模型；赵亚红等^[11]提出用径向基神经网络修正无偏灰色预测残差，预测更精确。单一预测方法难以准确预测出回采工作面瓦斯涌出量的实际变化趋势，由于影响回采工作面瓦斯涌出的因素非常多，不同工况下的影响因素也有所差异，需要找出一种能够反映影响因素与回采工作面瓦斯涌出量之间复杂的非线性关系的预测模型。部分学者将多种预测算法结合起来进行研究^[12-14]，结果表明，与单一预测方法相比，此类方法获得了更接近实际的效果，为解决回采工作面瓦斯涌出量预测问题提供了新思路。

将灰色模型与BP神经网络相结合的方法在保留灰色理论优势的同时，还弥补了忽视影响因素的不足，整体预测结果在预测精度和非线性变化方面优势明显^[15]；此外，对于工作面回风瓦斯体积分数的预测研究鲜有报道，为此，在此组合模型的基础上以SSA为核心进行优化，考虑了瓦斯抽采情况下回采工作面瓦斯涌出量和工作面回风瓦斯体积分数的变化趋势，构建了ISSA-GM-BP模型并进行应用，提高了模型精度和运算速度；研究结果对矿井瓦斯涌出量及其回风瓦斯体积分数预测与日常治理具有重要的现实意义。

1.   麻雀搜索算法改进原理

1.1   麻雀搜索算法

麻雀搜索算法（SSA）是 一种基于自然界麻雀种群捕食与反捕食行为的智能优化算法，通过对麻雀群体寻找食物和逃避被捕猎的行为进行研究，将不同的麻雀个体分为发现者、加入者、预警者3类，采用不同移动规则迭代更新麻雀个体位置，以实现智能优化目标。在 SSA 算法中，种群中$n$只麻雀在$d$维解空间的初始位置如式（1）所示^[16]：

麻雀种群的适应度值表示如式（2）：

式中：${F_X}$为适应度函数；${X_i}$为第$i$只麻雀的位置；$f\left( {{X_i}} \right)$为麻雀个体的适应度值。

在每次迭代的过程中，发现者的位置更新描述如式（3）：

式中：$t$为当前的迭代数；$j = 1,2,3, \cdots ,d$；${\mathrm{ite}}{{\mathrm{r}}_{\max }}$为1个常数，表示最大的迭代次数；${X_{ij}}$为第$i$个麻雀在第$j$维中的位置信息；$\omega \in \left( {0,1} \right]$为1个随机数；${R_2}\left( {{R_2} \in \left[ {0,1} \right]} \right)$、${\mathrm{ST}}\left( {{\mathrm{ST}} \in \left[ {0.5,1} \right]} \right)$分别为预警值和安全值牌；$Q$为服从正态分布的随机数；${\boldsymbol{L}}$为$l \times d$的矩阵，其中该矩阵内每个元素全部为1。

加入者的位置更新描述如式（4）：

式中：${X_p}$为目前发现者所占据的最优位置；${X_{{\mathrm{worst}}}}$为当前全局最差的位置；${\boldsymbol{A}}$为1个$l \times d$的矩阵，其中每个元素随机赋值为1或−1，并且${{\boldsymbol{A}}^ + } = {{\boldsymbol{A}}^{\mathrm{T}}}{\left( {{\boldsymbol{A}}{{\boldsymbol{A}}^{\mathrm{T}}}} \right)^{ - 1}}$；当$i > \dfrac{n}{2}$时，表明适应度值较低的第$i$个加入者需要飞往其它地方觅食，以获得更多的能量。

选取每代产生的新种群的 10%～20%个体作为预警者负责警戒，其位置更新如式（5）：

式中：${X_{{\mathrm{best}}}}$为当前的全局最优位置；$\beta$为步长控制参数，是服从均值为0、方差为1的正态分布的随机数；$K \in \left[ { - 1,1} \right]$为1个随机数；${f_i}$为当前麻雀个体的适应度值；${f_{\mathrm{g}}}$、${f_{\mathrm{w}}}$分别为当前全局最佳和最差的适应度值；$\varepsilon$为最小的常数，以避免分母出现0。

1.2   Chebyshev 混沌映射

麻雀搜索算法对群体执行初始化时采用随机生成的方式，这使得麻雀种群内的个体初始位置分配不均衡。利用Chebyshev混沌映射^[17]的类随机性、空间遍历性和非重复性对种群进行初始化，跳出局部极值点的可能性相对更大，提高算法搜索速度。

$\lambda$阶Chebyshev映射表达式如式（6）^[17]：

式中：${c_i}$为$i$时刻的混沌映射数值，是1个把区间$\left[ { - 1,1} \right]$映射到区间$\left[ { - 1,1} \right]$的满映射。

1.3   动态惯性权重

SSA 算法机制容易出现因忽略搜索盲点和搜索范围不足而陷入局部极值，在发现者位置更新公式中引入动态变化的惯性权重$\varphi$，然后对式（3）中发现者位置$X_{i,j}^t$的参与程度进行动态调控，尤其在迭代后期使发现者可以更加有效地进行局部搜索，加强了算法在解空间的邻域搜索能力^[18]。新的发现者位置更新公式及$\varphi$的计算式如式（7）和式（8）所示：

式中：${\varphi _1}$、${\varphi _2}$为权重调整参数，设置${\varphi _1} = 0.9$，${\varphi _2} = 0.4$。

1.4   Lévy 飞行策略

Lévy飞行是一种特殊的随机游走策略，它的游走步长分布服从重尾特征的概率分布，称为Lévy分布，其通常可以近似看作一个简单的幂函数分布$L(s) \sim {\left| s \right|^{ - 1 - \beta }}$，其中$0 < \beta \leqslant 2$，$s$为步长，$L(s)$为移动步长$s$的概率^[19-20]。因此Lévy分布可以表示为式（9）：

式中：$\mu > 0$为最小步长；$\gamma$为规模参数。

明显地，当$s \to \infty$时， 式（9）可写成式（10）：

通常情况下，将$L(s)$近似看作式（11）：

式中：$\Gamma$为gamma函数。

在Mantegna等的算法中，可以将Lévy飞行步长定义为式（12）：

式中：$s$为Lévy飞行路径；$u$、$v$为符合正态分布的随机数，$u \sim N(0,\sigma _v^2)$，$v \sim N(0,\sigma _u^2)$。

${\sigma _u}$、${\sigma _v}$由式（13）得到：

式中：β的范围为0~2，一般取$\beta = 1.5$。

2.   ISSA-GM-BP模型的建立

2.1   影响因素分析

从初始瓦斯条件、煤层地质条件、开采条件3个方面分析回采工作面瓦斯涌出量的影响因素。

1）初始瓦斯条件。煤层本身的瓦斯含量是最直接影响瓦斯涌出量的关键因素，较高的瓦斯含量意味着更多的瓦斯可以从煤层中释放出来；邻近煤层瓦斯会通过煤层的孔裂隙向本煤层扩散或渗流，邻近煤层厚度越大，采动影响卸压程度越高，瓦斯扩散或渗流作用随着邻近煤层瓦斯含量的增加而增强。

2）煤层地质条件。煤层埋藏深度、厚度、倾角以及邻近煤层间距都会对回采工作面的瓦斯涌出产生影响，煤层埋藏深度越大，地应力与温度随之增大，从而提高了煤层瓦斯涌出的概率；较厚的煤层为瓦斯储存提供更大的空间，较小的煤层间距可以加速邻近煤层瓦斯在煤岩层之间扩散；煤层倾角会改变瓦斯的运移路径，倾角越大，瓦斯越容易沿煤层倾斜的方向扩散或渗流。

3）开采条件。主要包括矿井开采的速度和环境，日产量直接与开采强度相关，较高的日产量通常意味着更大的开采强度，这会导致更大的地应力释放和煤岩破碎，不仅增加瓦斯涌出的可能性还会提高瓦斯涌出的速率；在高瓦斯矿井开采中，优化通风系统和采取合适的抽采措施是常见的瓦斯治理策略，同时它们也会给瓦斯涌出带来不同的影响。合理控制供风量和瓦斯抽采量都可以降低回采工作面瓦斯涌出。

以上影响因素通过回采工作面瓦斯涌出量影响工作面回风瓦斯体积分数变化。以黑龙江某矿3^#煤层为例，该矿地质构造复杂、断层多且为高瓦斯矿井，根据上述分析结果，对各影响因素进行灰色关联分析。灰色关联分析结果见表1。

表  1  灰色关联分析结果

Table  1.  Results of grey relational analysis

影响因素	关联度
	回采工作面瓦斯 涌出量（Y1）	工作面回风CH4体积 分数（Y2）
工作面供风量（X1）	0.6721	0.8400
瓦斯抽采量（X2）	0.7645	0.6184
工作面日产量（X3）	0.6312	0.6332
煤层埋藏深度（X4）	0.7755	0.7857
煤层厚度（X5）	0.7239	0.7441
煤层倾角（X6）	0.7685	0.6739
邻近煤层间距（X7）	0.7966	0.7053
原始瓦斯含量（X8）	0.8205	0.7617
邻近煤层厚度（X9）	0.6993	0.7842
邻近层瓦斯含量（X10）	0.8151	0.7501

下载: 导出CSV 

| 显示表格

由表1可知：影响回采工作面瓦斯涌出量的因素中，关联度大小排序为X₈>X₁₀>X₇>X₄>X₆>X₂>X₅>X₉>X₁>X₃，且均大于0.6，与回采工作面瓦斯涌出量具有较强的相关性；影响工作面回风瓦斯体积分数的因素中，关联度大小排序为X₁>X₄>X₉>X₈>X₁₀>X₅>X₇>X₆>X₃>X₂，且均大于0.6，与工作面回风瓦斯体积分数具有较强的相关性。

最终将影响回采工作面瓦斯涌出量Y₁、工作面回风瓦斯体积分数Y₂的样本数据确定为包括以下10个具有代表性且易于量化表达的影响因素的20组数据：工作面供风量X₁、瓦斯抽采量X₂、工作面日产量X₃、煤层埋藏深度X₄、煤层厚度X₅、煤层倾角X₆、邻近煤层间距X₇、原始瓦斯含量X₈、邻近煤层厚度X₉、邻近层瓦斯含量X₁₀。将收集到的20组回采工作面瓦斯涌出量、工作面回风瓦斯体积分数及影响因素数据作为模型样本集，该20组数据是黑龙江某矿3^#煤层连续20个月的月末实测数据，样本数据见表2。

表  2  回采工作面瓦斯涌出量和工作面回风瓦斯体积分数及影响因素数据

Table  2.  Gas emission from mining face, CH₄ volume fraction in return air of working face, and influencing factors data

序号	X1/(m3·min−1)	X2/(m3·min−1)	X3/t	X4/m	X5/m	X6/（°）	X7/m	X8/(m3·t−1)	X9/m	X10/(m3·t−1)	Y1/(m3·min−1)	Y2/%
1	1260	34.4	1786	732.0	1.88	14	31	1.03	0.83	3.26	39.44	0.45
2	1140	30.9	2010	739.1	1.89	14	37	0.94	0.98	3.36	36.60	0.50
3	1370	27.4	1843	729.2	1.85	12	34	1.01	1.09	3.23	36.99	0.47
4	1050	31.8	1606	723.9	1.47	15	35	0.91	1.16	2.95	33.90	0.49
5	1200	23.9	1366	728.9	1.91	11	33	0.83	1.25	3.21	32.30	0.57
6	1218	23.1	2066	710.0	1.51	14	30	0.81	1.23	2.92	29.19	0.54
7	1192	24.1	1255	717.4	1.33	16	32	0.88	1.11	2.91	30.06	0.56
8	1240	20.8	1194	720.4	1.68	13	31	0.84	1.07	2.89	29.48	0.61
9	1290	21.1	1681	708.1	1.42	14	27	0.83	1.15	2.79	28.84	0.58
10	1460	18.8	2120	725.0	1.86	12	29	0.85	0.99	2.98	29.02	0.62
11	1200	23.3	2007	703.1	1.52	14	33	0.84	1.03	2.74	30.50	0.61
12	1430	17.6	1094	690.3	1.54	13	26	0.86	1.15	2.78	27.61	0.65
13	1279	18.2	1681	692.1	1.63	10	31	0.82	1.14	2.67	25.87	0.62
14	1187	20.7	1078	687.8	1.35	16	28	0.88	1.02	2.84	27.80	0.63
15	1270	15.2	1692	694.7	1.73	10	22	0.78	1.59	2.77	24.09	0.69
16	1280	14.7	1606	692.5	1.45	10	35	0.82	1.07	2.62	23.66	0.66
17	1438	13.8	1000	686.5	1.69	11	24	0.75	1.22	2.75	23.90	0.70
18	1520	15.1	894	687.0	1.60	11	19	0.77	1.05	2.77	25.74	0.71
19	900	19.8	1172	690.9	1.15	10	33	0.76	0.94	2.62	22.50	0.70
20	1406	13.4	1414	688.9	1.63	11	21	0.73	1.14	2.77	23.24	0.72

下载: 导出CSV 

| 显示表格

2.2   动态灰色GM(1，1，$\alpha$)模型

传统的GM(1，1)模型建立原理是在原始数列累加得到新序列后，生成紧邻均值序列，建立微分方程，将方程的解序列进行累减运算后获取预测值。采用动态生成系数$\alpha$，替代紧邻均值序列中的固定值0.5，通过动态调整各区间的生成系数$\alpha$，降低灰色模型的背景值误差。

在建立灰色差分方程时，确定原始序列${X^{(1)}} = \left\{ {{x^{(1)}}(k),(k = 2,3, \cdots ,n)} \right\}$的紧邻均值序列${Z^{(1)}} = \left\{ {{z^{(1)}}(k),(k = 2,3, \cdots ,n)} \right\}$，其中${Z^{(1)}}$满足式（14）：

式中：动态生成系数$\alpha (k) \in [0,1]$。

2.3   ISSA-GM-BP模型

矿井回采工作面瓦斯涌出量、工作面回风瓦斯体积分数受到多种因素的影响，呈现出波动大、随机性强的特点，灰色预测精度大大降低，加之实测资料有限，导致数据体量较小，难以直接通过BP神经网络进行训练拟合。将灰色预测与BP神经网络组合使用可以克服上述难题。引入Chebyshev 混沌映射、动态惯性权重和Lévy 飞行策略后，改进麻雀搜索算法（ISSA）的收敛速度和全局搜索能力得到提升。利用ISSA分别对灰色预测和BP神经网络进行算法寻优，从而提升组合预测ISSA-GM-BP模型的准确性。

确定一个合理的适应度函数是应用ISSA对灰色预测进行算法优化的关键^[21]。选取预测数据${\hat x^{(0)}}(k)$与原始数据${x^{(0)}}(k)$的最大相对误差为适应度函数对动态生成系数$\alpha$进行寻优，如式（15）所示，以解算最优灰色差分方程，使得GM(1,1,$\alpha$)预测结果更为精确。

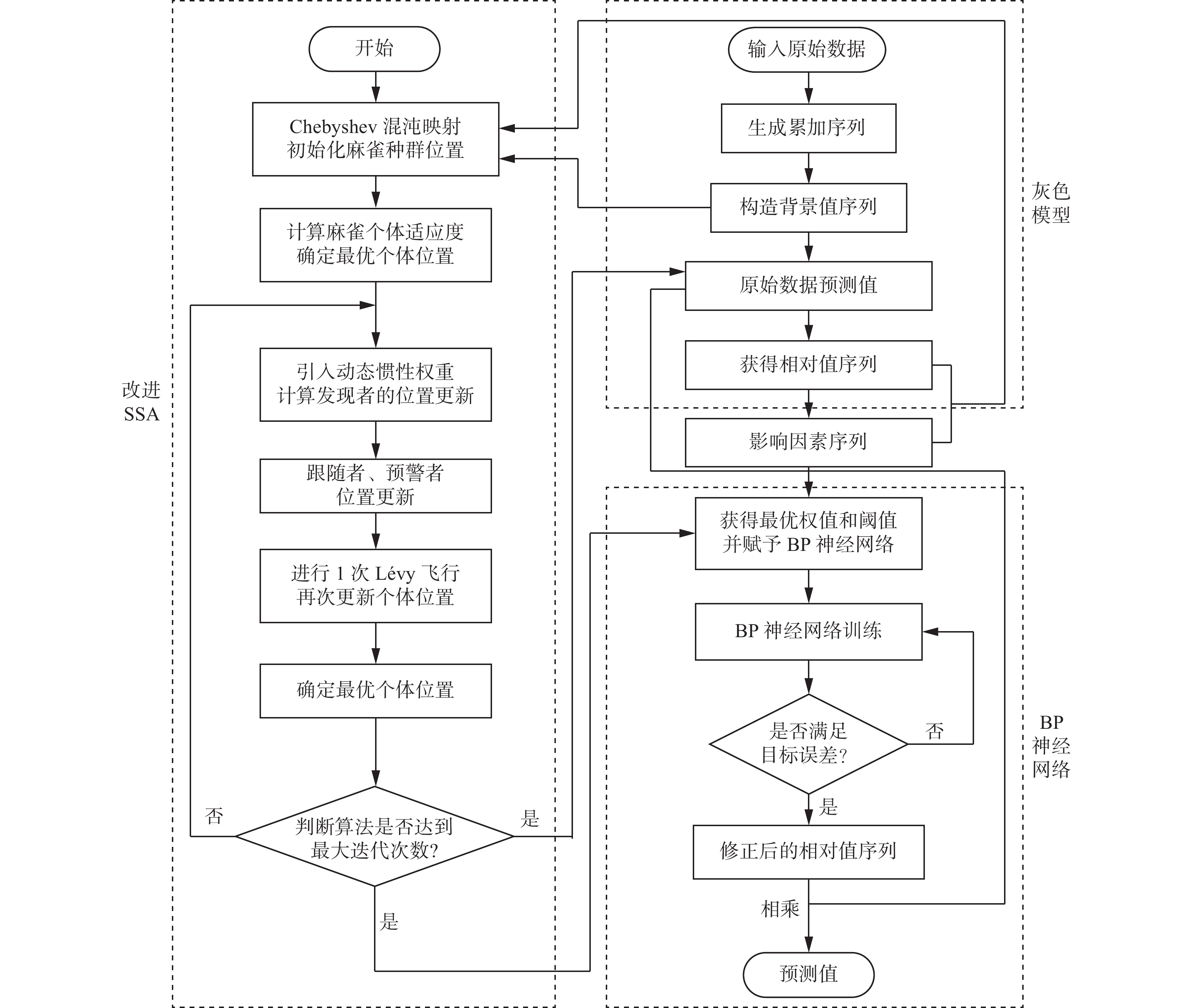
采用 BP 神经网络预测时，训练集数量保持不变的情况下，影响预测精度的主要因素为 BP 神经网络初始化权值和阈值2项参数。 该参数的取值通常由 BP 算法随机生成或者通过操作者手动进行调试，从而导致构建的 BP 神经网络模型预测精度低、收敛速度慢，甚至出现“过拟合”。鉴于此，利用改进的 SSA 对 BP 神经网络的权值和阈值进行优化。ISSA-GM-BP模型预测流程如图1所示。

图  1  ISSA-GM-BP模型预测流程

Figure  1.  ISSA-GM-BP model prediction process

下载: 全尺寸图片 幻灯片

ISSA-GM-BP模型的建模过程如下：

1）建立动态灰色GM(1，1，$\alpha$)模型，对原始序列${X_k}^{(0)}$进行预测，得到预测序列${\hat X_k}^{(0)}$。

2）将动态灰色GM(1，1，$\alpha$)模型原始序列${X_k}^{(0)}$与预测序列${\hat X_k}^{(0)}$相比，计算得到相对值序列${M_k}$。

3）将各影响因素序列作为输入层同时输入权值和阈值优化后的 BP 神经网络，对作为输出层的相对值序列${M_k}$进行修正，预测序列${\hat X_k}^{(0)}$与修正后的相对值序列${M_k}^{(1)}$相乘得到ISSA-GM-BP模型预测值${X_k}$。

3.   模型预测结果

3.1   模型参数设置

利用 MATLAB 实现ISSA-GM-BP模型、SSA-BP神经网络和BP 神经网络3种预测模型，分别运用3种模型对回采工作面瓦斯涌出量及工作面回风瓦斯体积分数进行预测，并对比预测结果和性能评价指标。

BP神经网络参数设定：输入层节点为10个，分别为工作面供风量、瓦斯抽采量、工作面日产量、煤层埋藏深度、煤层厚度、煤层倾角、邻近煤层间距、原始瓦斯含量、邻近煤层厚度、邻近层瓦斯含量；隐含层节点数为6；输出层节点为 2个，分别为回采工作面瓦斯涌出量、工作面回风瓦斯体积分数实际值与灰色预测值的相对值；训练次数1000次，目标误差10⁻⁶。ISSA-GM-BP模型预测计算过程中，ISSA优化包含2个模块：灰色预测模块初始种群规模为70，最大迭代次数设为 50 次，预警者数量取种群数目的 20%，预警值 0.6；BP神经网络模块初始种群规模为30， 最大迭代次数设为30次，预警者数量取种群数目的30%，预警值0.6。

经大量模型训练发现，当预测样本占整个样本集的比例超过80%后，随着预测样本数据量增大，回采工作面瓦斯涌出量和工作面回风瓦斯体积分数预测结果的平均相对误差变化幅度均不超过0.5%。因此，选择数据前80%的部分作为训练集，剩余数据作为测试集可满足模型预测精度的要求。

3.2   预测结果对比分析

ISSA优化2个模块的适应度收敛曲线如图2、图3所示。

图  2  灰色预测模块适应度收敛曲线

Figure  2.  Fitness convergence curves of grey prediction module

下载: 全尺寸图片 幻灯片

图  3  BP神经网络模块适应度收敛曲线

Figure  3.  BP neural network module fitness convergence curves

下载: 全尺寸图片 幻灯片

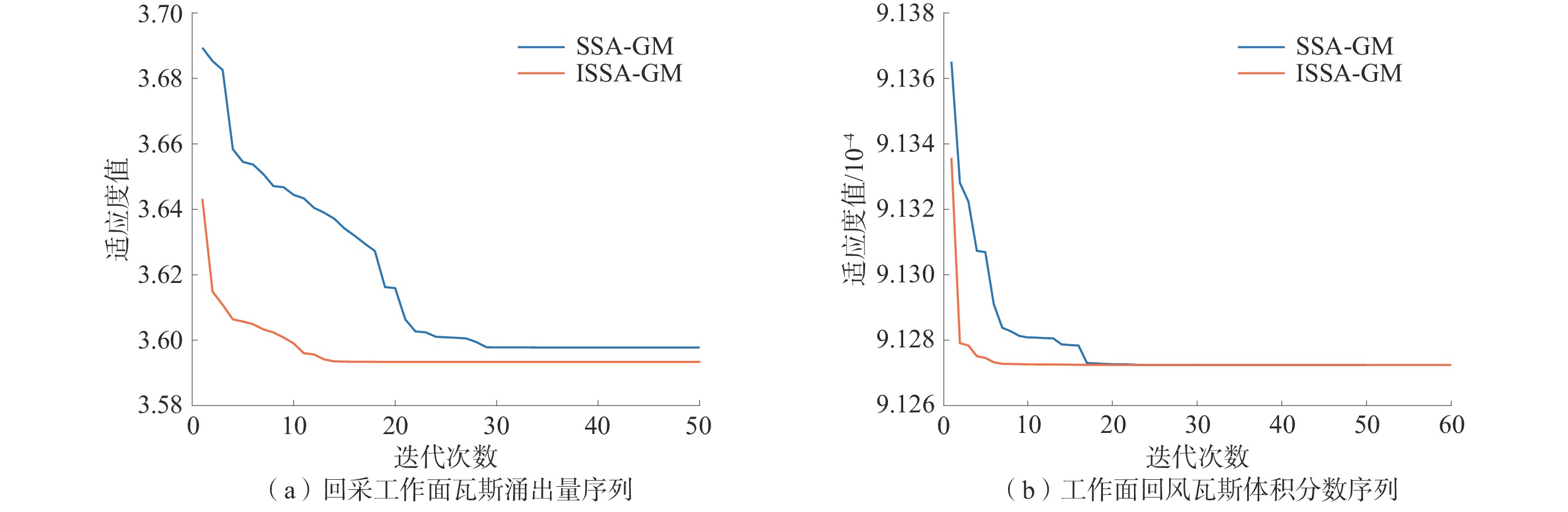
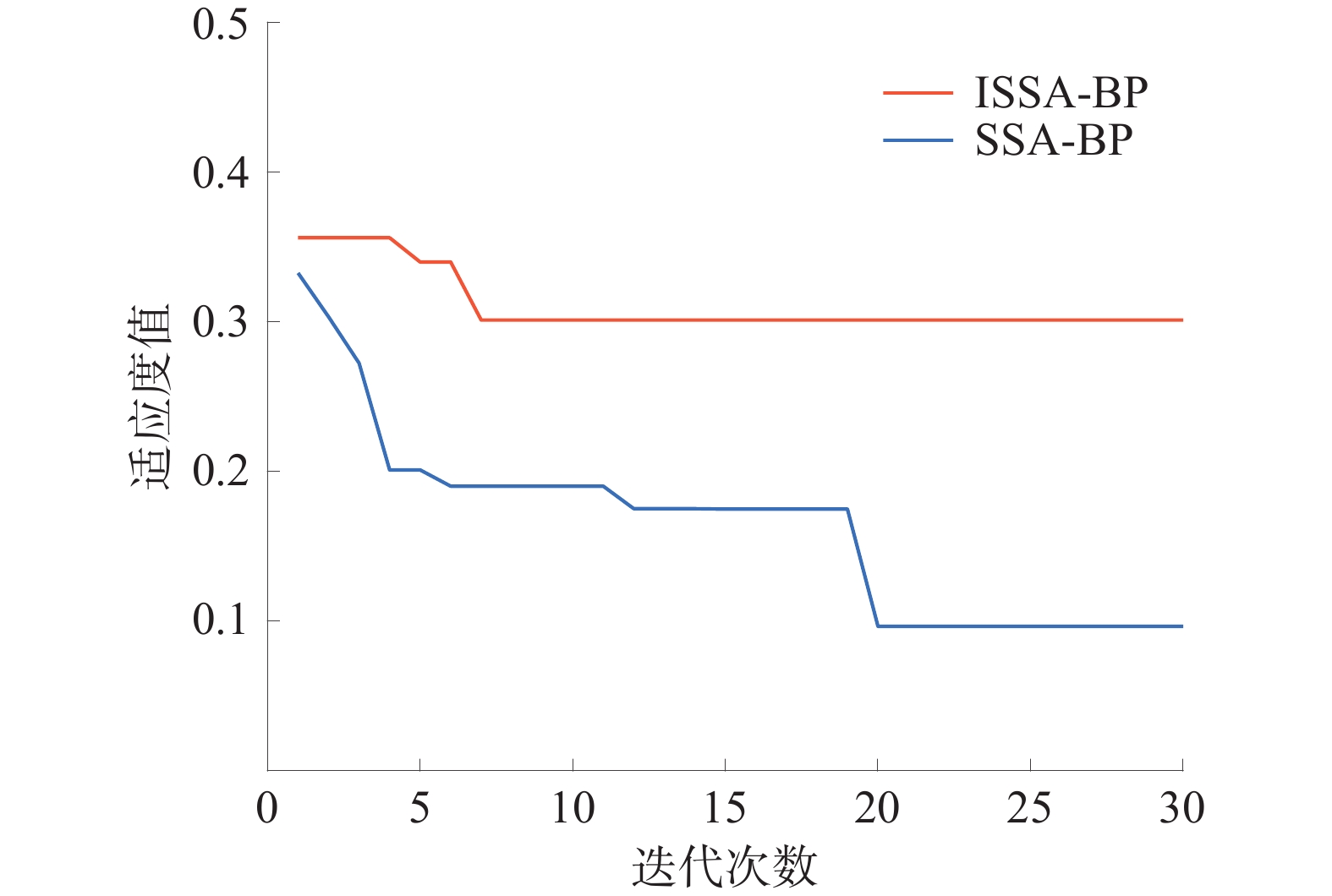
由图2、图3可知：ISSA-GM 模型分别在迭代13、8次后达到全局最优，ISSA-BP模型在迭代7次后达到全局最优，SSA经改进后全局搜索能力得到明显提升；ISSA-GM 模型训练的适应度值更低，具有更高的精确度，而ISSA-BP模型与SSA-BP模型由于训练样本不同而无法直接判定精确度高低，通过ISSA-GM-BP模型与其他模型预测结果的对比反映其优越性。

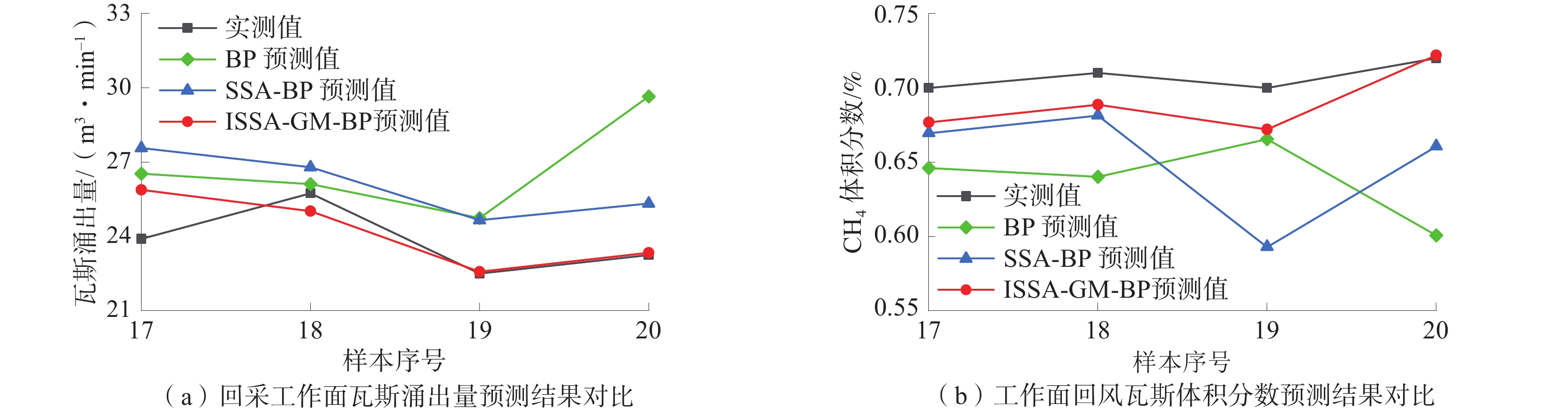
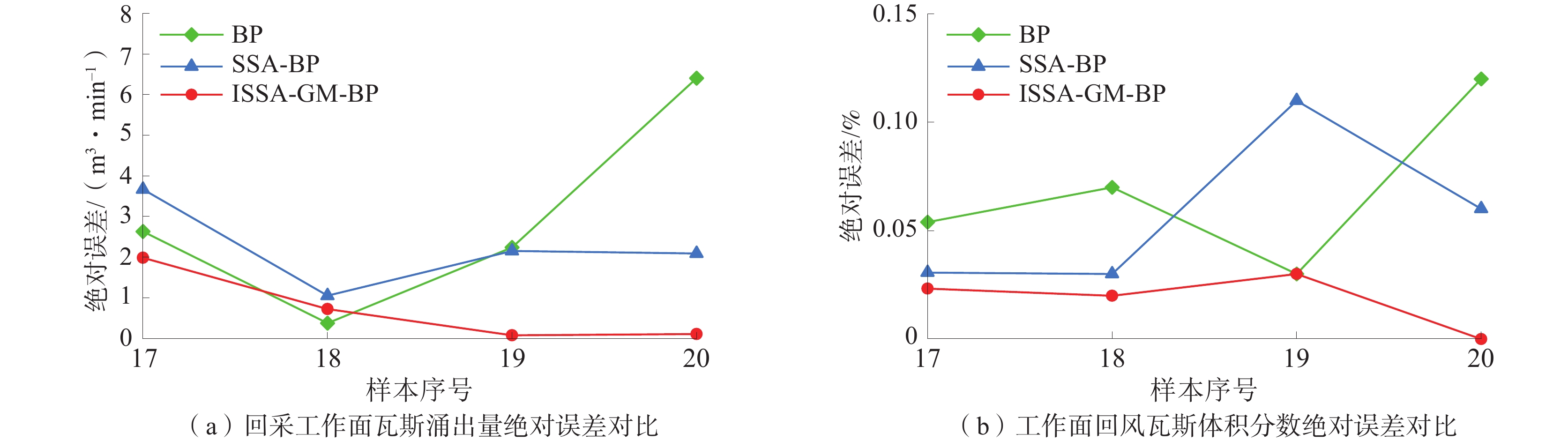
为验证 ISSA-BP 模型在回采工作面瓦斯涌出量及工作面回风CH₄体积分数预测方面的有效性和优越性，选取数据样本中的后4组数据作为预测样本进行预测，各模型的预测结果见表3，各模型预测值与实测值对比如图4所示，不同模型预测绝对误差如图5所示。

表  3  各模型预测结果

Table  3.  Prediction results of each model

序号	实际数据		BP神经网络		SSA-BP神经网络		ISSA-GM-BP模型
	Y1/(m3· min−1)	Y2/%	Y1/(m3· min−1)	Y2/%	Y1/(m3· min−1)	Y2/%	Y1/(m3· min−1)	Y2/%
17	23.90	0.70	26.53	0.65	27.57	0.67	25.88	0.68
18	25.74	0.71	26.11	0.64	26.79	0.68	25.02	0.69
19	22.50	0.70	24.74	0.67	24.65	0.59	22.57	0.67
20	23.24	0.72	29.65	0.60	25.33	0.66	23.34	0.72

下载: 导出CSV 

| 显示表格

图  4  不同模型预测结果对比

Figure  4.  Comparison of prediction results of different models

下载: 全尺寸图片 幻灯片

图  5  不同模型绝对误差对比

Figure  5.  Comparison of absolute errors of different models

下载: 全尺寸图片 幻灯片

在回采工作面瓦斯涌出量的预测中：ISSA-GM-BP模型整体预测值与实测值变化趋势十分接近，符合原始绝对瓦斯涌出量变化规律，表明组合模型经智能算法ISSA优化后对序列预测具有很好的适应性、精确度高；SSA-BP 神经网络模型预测值与实测值整体趋势接近，但存在较大误差；而BP 神经网络模型预测值总体趋势与实际相差大，样本20的预测值偏离实测值过多。在工作面回风瓦斯体积分数的预测中：ISSA-GM-BP模型和SSA-BP 神经网络模型整体预测值实测值变化趋势相似，但SSA-BP 神经网络模型预测值与实测值存在的偏差更大，BP 神经网络模型预测值样本偏离实际过多，预测效果较差。

在回采工作面瓦斯涌出量的预测中：ISSA-GM-BP模型的相对误差曲线平面位置高度明显低于SSA-BP 神经网络和BP神经网络，且变化较为平缓，预测结果准确度最高，ISSA-GM-BP模型预测绝对误差最大为1.98 m³/min，低于SSA-BP 神经网络的最大绝对误差3.67 m³/min和BP 神经网络的最大绝对误差6.41 m³/min。在工作面回风瓦斯体积分数的预测中：ISSA-GM-BP模型预测结果中每个样本的绝对误差均低于SSA-BP 神经网络和BP神经网络，绝对误差最小低至0.0019 m³/min。

由此表明，ISSA-GM-BP模型在回采工作面瓦斯涌出量及其回风瓦斯体积分数预测上具有可行性，而且预测结果误差小、稳定性高。

3.3   模型精度评价

选取平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、均方误差（MSE）、决定系数（R²）作为量化指标，对3种模型的预测效果进行评价^[22-23]。各模型评价指标见表4。

表  4  各模型评价指标

Table  4.  Evaluation indicators for each model

模型	MAE			MAPE			MSE			R2
	Y1	Y2		Y1	Y2		Y1	Y2		Y1	Y2
BP	2.9117	0.0694		12.490 0	9.760 0		13.2946	0.0058		0.5318	0.4619
SSA-BP	2.2412	0.0565		9.500 0	8.000 0		5.8932	0.0042		0.7924	0.6104
ISSA-GM-BP	0.7166	0.0186		2.950 0	2.650 0		1.1114	0.0004		0.9609	0.9587

下载: 导出CSV 

| 显示表格

由表3可知：在回采工作面瓦斯涌出量、工作面回风瓦斯体积分数预测结果中，ISSA-GM-BP模型的平均绝对百分比误差MAPE分别为2.95%、2.65%，比SSA-BP神经网络分别提高了6.55%、5.35%，比BP神经网络分别提高了9.54%、7.11%，准确度明显提高；ISSA-GM-BP模型的决定系数R²分别为0.9609、0.9587，相比于SSA-BP神经网络和BP 神经网络拟合度更高。综合4个量化指标来看，BP神经网络预测效果最差，这是由BP神经网络自身搜索能力差、计算速度低造成的。

因此，通过对比3个模型的评价指标，发现提出的ISSA-GM-BP模型精确度更高，各方面预测效果均最佳，可以满足瓦斯涌出量预测的需求。

4.   结　语

1）通过Chebyshev 混沌映射、动态惯性权重、Lévy飞行策略算法对SSA进行优化改进，以动态生成系数$\alpha$为核心建立动态灰色GM(1，1，$\alpha$)模型，克服了传统灰色模型因背景值固定而误差较大的问题，更能适应变化复杂、线性规律不明显的数据序列，从而提高预测准确性。

2）利用改进SSA优化BP神经网络并与动态灰色GM(1，1，$\alpha$ )模型相结合，建立起ISSA-GM-BP模型，加入多因素对原始序列的影响并解决了BP神经网络数据量需求大的问题，为此类监测样本少、多因素耦合变化的序列预测提供构建模型新思路。

3）基于ISSA-GM-BP模型对黑龙江某矿3^#煤层回采工作面瓦斯涌出量及其回风瓦斯体积分数进行了预测，与SSA-BP神经网络、BP 神经网络模型预测结果对比。结果表明，ISSA-GM-BP模型预测的数据与真实值误差更小且完全符合实际回采工作面瓦斯涌出量和工作面回风瓦斯体积分数变化趋势，验证了该模型的有效性与准确性。