Control mechanism of surface settlement in mining face by high and thick conglomerate
-
摘要:
为研究工作面开采后高位巨厚砾岩层对地表沉降的控制机理，以高庄煤矿西十一采区典型工作面为背景，采用理论分析、数值模拟、地表沉降实测等方法开展研究；基于微震事件分布分析了高位巨厚砾岩层工作面覆岩结构特征，高位巨厚砾岩层受采动影响较小，破坏程度较低；通过建立巨厚砾岩层Euler-Bernoulli 固支裂缝梁力学模型，推导了裂缝影响下挠曲变形方程，阐明了巨厚砾岩层对地表沉降控制机理。数值模拟结果显示：覆岩垂直位移在巨厚砾岩层底部发生突变，巨厚砾岩层底部易产生离层空间，离层空间经历了“月牙”形、“盘”形形态演化，巨厚砾岩层影响下的模型地表沉降量明显较小。地表沉降实测结果显示：高位巨厚砾岩区工作面开采地表沉降量明显更小，高位巨厚砾岩对地表沉降具有明显的控制作用。
-
关键词:
- 高位巨厚砾岩层 /
- 地表沉降 /
- Euler-Bernoulli 固支裂缝梁 /
- 控制机理 /
- 覆岩结构
Abstract:In order to study the control mechanism of surface subsidence by the high and huge thick conglomerate strata after working face mining, the typical working face of west 11th mining area of Gaozhuang Coal Mine is taken as the background, and the research is carried out by using the theoretical analysis, numerical simulation, and the actual measurement of surface subsidence; based on the distribution of micro-seismic events, we analyzed the characteristics of overlying strata structure in the working face of the high level huge-thick conglomerate layer, and the high level huge-thick conglomerate layer is less affected by mining, and the degree of fissure development is lower; a mechanical model of Euler-Bernoulli solid-supported cracked beam in giant conglomerate strata was established, and the deflection control equations under the influence of cracks were deduced, which elucidated the control mechanism of giant conglomerate strata on surface subsidence. Numerical simulation results show that the vertical displacement of overlying strata changes abruptly at the bottom of the giant conglomerate strata, the bottom of the giant conglomerate strata is prone to generating off-stratum space, and the off-stratum space undergoes the morphology evolution of “crescent” and “disk”, and the modeled surface subsidence under the influence of the giant conglomerate strata is significantly smaller than that of the giant conglomerate layer. The amount of modeled surface subsidence under the influence of the giant conglomerate layer is significantly smaller. The measured results of surface subsidence show that the amount of surface subsidence of the working face mining in the high level giant thick conglomerate area is obviously smaller, and the high level giant thick conglomerate has an obvious controlling effect on surface subsidence.
-
地下开采引起环境问题大多与开采造成的岩层和地表移动有关，开采沉陷常造成土地塌陷或积水、道路塌陷等矿区环境灾害[1-2]。地表沉降受地质条件和开采条件影响，如上覆岩层性质、煤层倾角、开采深度和厚度、断层及其他弱面、重复采动、采空区面积等，地质条件是矿山开采岩层移动的基础，决定地表塌陷的类型与过程[3-4]。地表沉降是松散层与覆岩关键层运动耦合的结果，岩层运动传递至地表引起地表沉降，形成沉陷盆地。覆岩主关键层对地表移动的动态过程起控制作用[5-7]，是影响地表沉降的重要因素。工作面开采后，覆岩呈“倒漏斗形”破坏，向上裂隙带横向范围逐渐减小，高位岩层破坏程度小，工作面覆岩巨厚砾岩层为主关键层，对上覆岩层是较稳定的支撑结构。根据高庄历史地表沉降观测记录，在西五、西三无巨厚砾岩层采区地表沉降明显大于上覆岩层分布高位巨厚砾岩层西十一采区，巨厚砾岩层对地表沉降具有重要影响。
张广超等[8]、王跃宗等[9]、孙庆先等[10]、柴敬等[11]针对厚硬关键层岩层采场地表沉降响应规律进行了研究，将地表沉降阶段划分为缓慢下沉阶段、急剧下沉阶段、稳定阶段，得出坚硬顶板对上覆岩层起主要控制作用形，坚硬关键层顶板导致地表沉陷；李想等[12]研究了深部采煤覆岩移动和地表沉降规律，结果表明，地表沉降曲线呈“U”字形，且在煤层回采过程中，沉降速率逐渐增大；王利[13]研究了巨厚覆岩下开采地表沉陷特征，得出巨厚覆岩下开采地表存在连续性变形的下沉与反弹，以及非连续性变形的地表斑裂现象；李春意等[14-15]研究了大采深巨厚砾岩开采条件下地表形变规律，结果表明，受关键层的控制，在整个观测过程中，地表始终处于缓慢下沉状态，且在沉降过程中不存在下沉突变点，巨厚砾岩层的悬臂支承作用是造成地表沉陷盆地出现偏态下沉的根本原因；关军琪等[16]研究了受地形条件影响下不同充填方案对覆岩及地表变形规律的影响，结果表明，间隔式充填能改变地表沉降盆地的形态,在充填量保持一定时，间隔式充填方案地表沉降量更小；曹琰波等[17]研究了双煤层开采条件下浅埋煤层覆岩破坏特征及地表沉降规律，结果表明，煤层开采时地表呈台阶式下沉，煤层厚度与地表沉降值呈正相关性；杨军伟等[18]研究了厚松散层矿区采动程度对地表沉降特征的影响，结果表明，厚松散层条件下，随着走向采动程度的不断加大，走向方向拐点逐渐由煤壁侧过渡到采空区侧。上述研究针对厚硬岩层、巨厚砾岩层工作面地表移动规律等开展了大量研究，但对于高位巨厚砾岩层对工作面开采地表沉降控制机理研究较少。为此，以高庄煤矿典型的高位巨厚砾岩，西十一采区为背景，采用理论分析、数值模拟，建立力学模型，研究裂隙控制下巨厚砾岩的变形，并结合现场地表沉降实测数据阐明巨厚砾岩对地表沉降的控制机理。
1. 工程背景
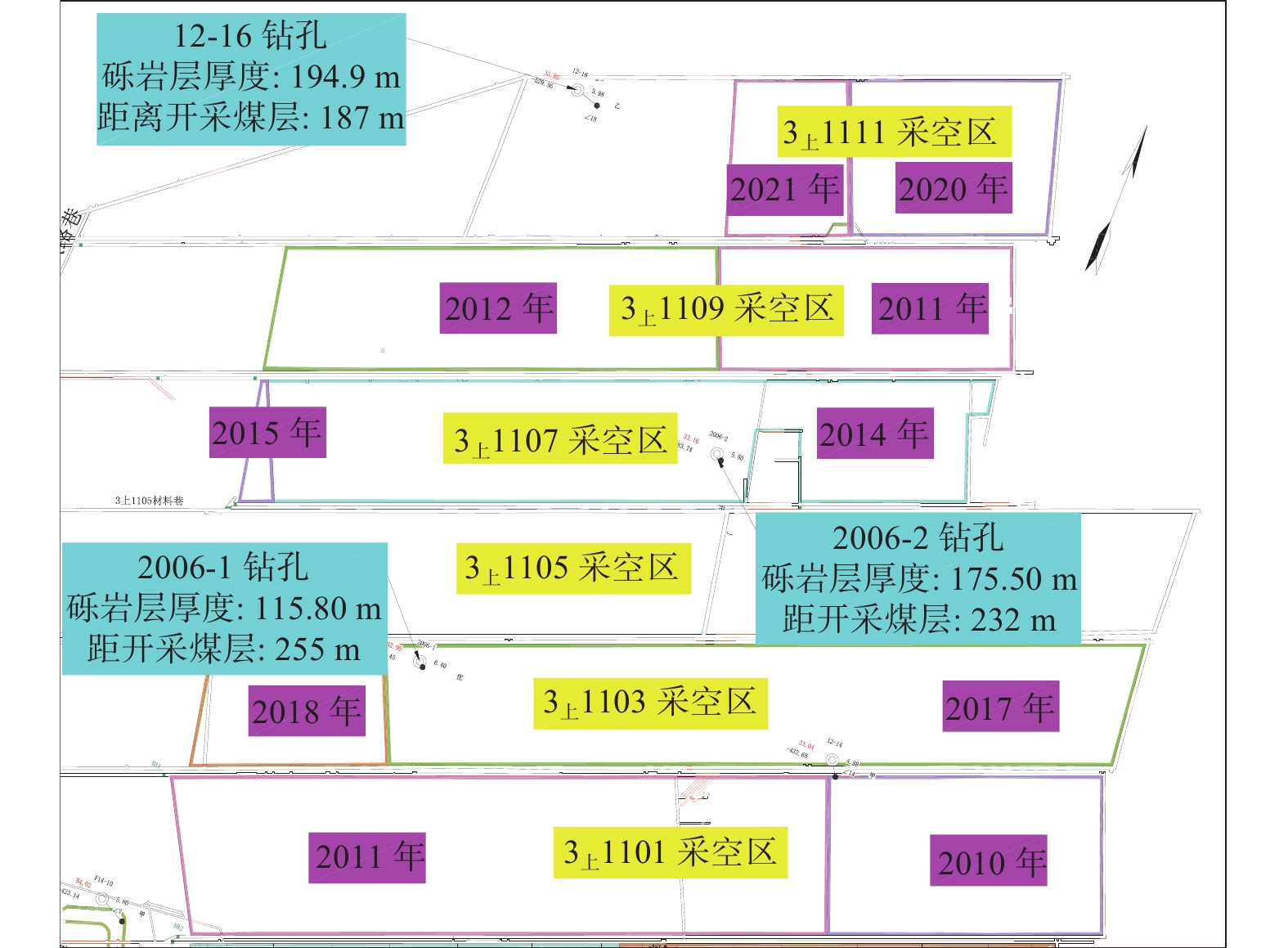
枣庄煤田高庄煤矿主采3上、3下两层煤，西十一采区为矿井主要采区，采区埋深约330~680 m。西十一采区总体上呈一单斜构造，岩层走向40°左右，倾向330°左右，倾角13°～16°，一般14°左右，产状比较稳定。西十一采区地层由老到新依次为奥灰、石炭系本溪群、石炭系太原群、二叠系山西组、二叠系下石盒子组、侏罗系砾岩及第四系。3煤层位于二叠系山西组，地层第四系之下分布侏罗系巨厚砾岩层，单斜构造及砾岩层位造成了厚度分布差异较大，厚度21.6~340.3 m，平均厚度255 m，向着单斜构造倾向方向逐渐变薄至西五采区尖灭，西十一采区东翼开采情况及巨厚砾岩层分布情况如图1所示，顶板地层统计见表1~表3。选取西十一采区东翼高位赋存巨厚砾岩层3上1111、3上1103典型工作面开展研究。
表 1 12-16钻孔顶板地层统计表Table 1. Stratigraphic statistics for roof of drill hole 12-16序号 岩性 厚度/m 序号 岩性 厚度/m 53 松散层 89.00 27 粗砂岩 5.37 52 粉砂岩 63.45 26 泥岩 2.28 51 砾岩 2.75 25 粉砂岩 1.90 50 泥岩 12.90 24 粗砂岩 6.85 49 砾岩 194.90 23 粉砂岩 8.27 48 泥岩 2.90 22 中砂岩 0.76 47 细砂岩 1.57 21 粉砂岩 1.62 46 泥岩 0.76 20 中砂岩 1.71 45 细砂岩 0.76 19 泥岩 6.37 44 泥岩 9.61 18 细砂岩 1.28 43 粉砂岩 6.90 17 粉砂岩 2.19 42 泥岩 7.94 16 中砂岩 2.95 41 细砂岩 1.33 15 泥岩 1.88 40 泥岩 3.42 14 粉砂岩 4.23 39 中砂岩 3.90 13 细砂岩 1.81 38 泥岩 9.61 12 粉砂岩 2.90 37 细砂岩 0.57 11 泥岩 4.95 36 泥岩 5.47 10 粉砂岩 3.52 35 细砂岩 6.23 9 细砂岩 0.86 34 煤层 0.19 8 粉砂岩 3.80 33 泥岩 5.99 7 细砂岩 1.05 32 煤层 0.32 6 泥岩 4.57 31 泥岩 2.91 4 粉砂岩 3.42 30 粉砂岩 5.94 3 细砂岩 1.66 29 泥岩 21.40 2 中砂岩 10.93 28 粉砂岩 3.52 1 3上煤层 3.98 表 2 2006-2钻孔顶板地层统计表Table 2. Stratigraphic statistics for roof of drill hole 2006-2序号 岩性 厚度/m 序号 岩性 厚度/m 27 松散层 104.45 13 中砂岩 7.25 26 砾岩层 175.50 12 砂质泥岩 13.60 25 砂质泥岩 10.20 11 中砂岩 20.65 24 中砂岩 22.15 10 砂质泥岩 9.85 23 砂质泥岩 1.40 9 中砂岩 5.95 22 细砂岩 8.40 8 砂质泥岩 7.40 21 中砂岩 12.85 7 中砂岩 3.85 20 砂质泥岩 28.95 6 砂质泥岩 5.00 19 中砂岩 5.40 5 中砂岩 3.20 18 砂质泥岩 2.65 4 砂质泥岩 4.00 17 煤 0.35 3 中砂岩 7.65 16 砂质泥岩 15.20 2 泥岩 1.20 15 细砂岩 7.30 1 3上煤层 5.50 14 砂质泥岩 13.45 表 3 2006-1钻孔顶板地层统计表Table 3. Stratigraphic statistics for roof of drill hole 2006-1序号 岩性 厚度/m 序号 岩性 厚度/m 31 松散层 110.65 15 中砂岩 8.00 30 砾岩 115.80 14 砂质泥岩 7.70 29 砂质泥岩 5.35 13 中砂岩 6.50 28 中砂岩 21.50 12 砂质泥岩 12.65 27 砂质泥岩 8.60 11 中砂岩 7.85 26 中砂岩 8.85 10 砂质泥岩 6.15 25 砂质泥岩 50.35 9 中砂岩 20.10 24 煤 0.35 8 砂质泥岩 1.95 23 砂质泥岩 0.75 7 中砂岩 4.55 22 细砂岩 4.95 6 砂质泥岩 0.65 21 砂质泥岩 9.05 5 中砂岩 5.00 20 细砂岩 5.65 4 砂质泥岩 0.95 19 中砂岩 5.85 3 中砂岩 11.80 18 砂质泥岩 22.45 2 泥岩 2.45 17 中砂岩 14.05 1 3上煤层 6.40 16 砂质泥岩 0.45 3上1111工作面埋深520~680 m，平均走向长度450 m，倾斜长度210 m，煤厚4.0～6.0 m，平均5.2 m，工作面回采一侧为3上1109采空区，工作面内地质钻孔煤层距离顶板巨厚砾岩层约187 m，砾岩层厚度194.9 m。
3上1103工作面埋深450~500 m,平均走向长度1 360 m，倾斜长度170 m，煤厚4.4～6.4 m，平均5.3 m，工作面回采一侧为3上1101采空区，工作面内地质钻孔显示煤层距离顶板巨厚砾岩层约255 m，砾岩层厚度115.8 m。
2. 高位巨厚砾岩工作面开采覆岩结构特征
大量研究表明[19-21]，微震可以反映采动上覆岩层损伤、破坏情况。采动影响下上覆岩层破坏以微震应力波形式释放弹性应变能，多个微震探头监测到微震应力波，可以定位微震震源，及按照衰减系数可以得到震源能量大小。因此，借助3上1111工作面微震事件震源在高度上能量及位置的分布，分析得到工作面开采覆岩结构大致特征。
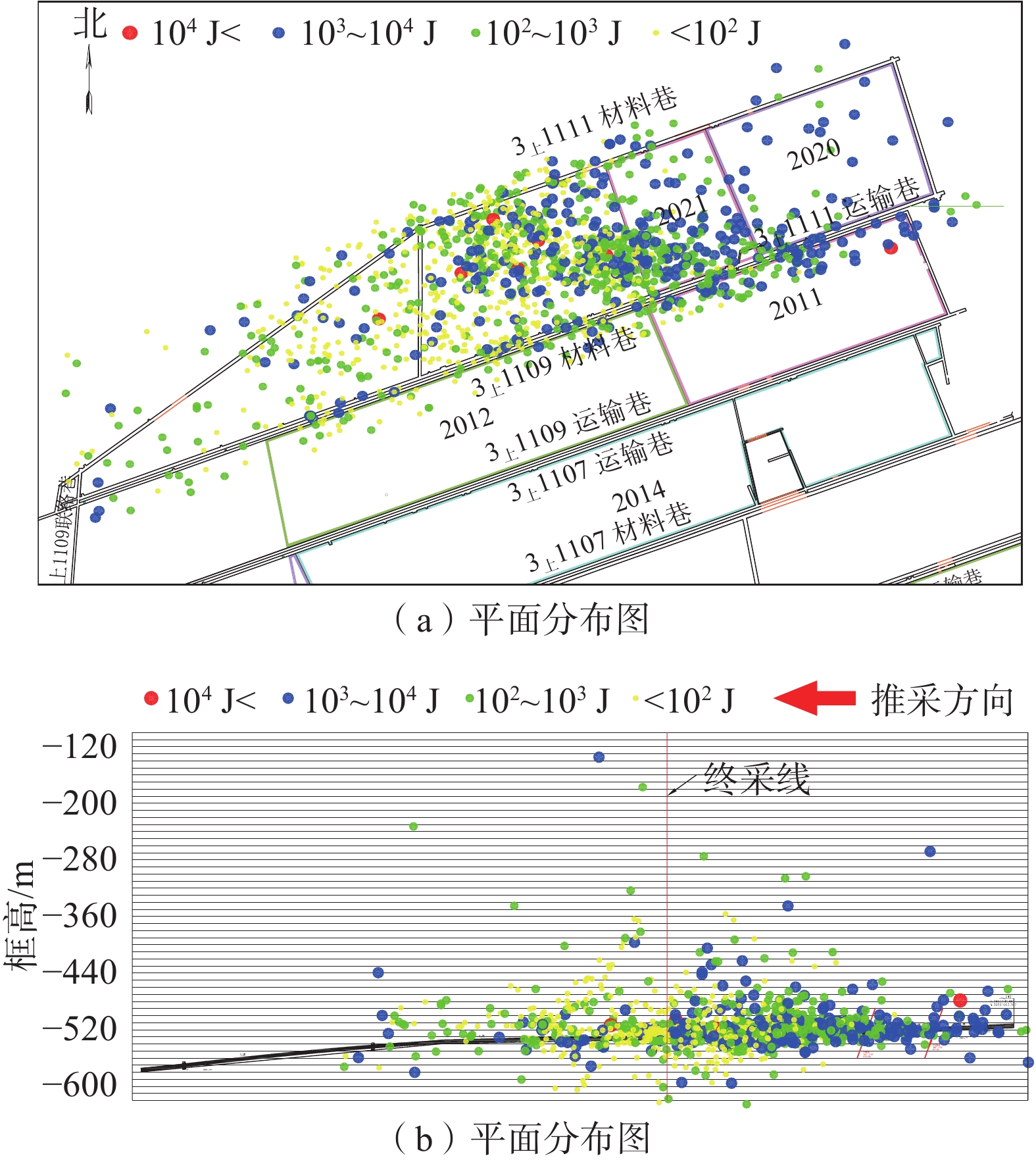
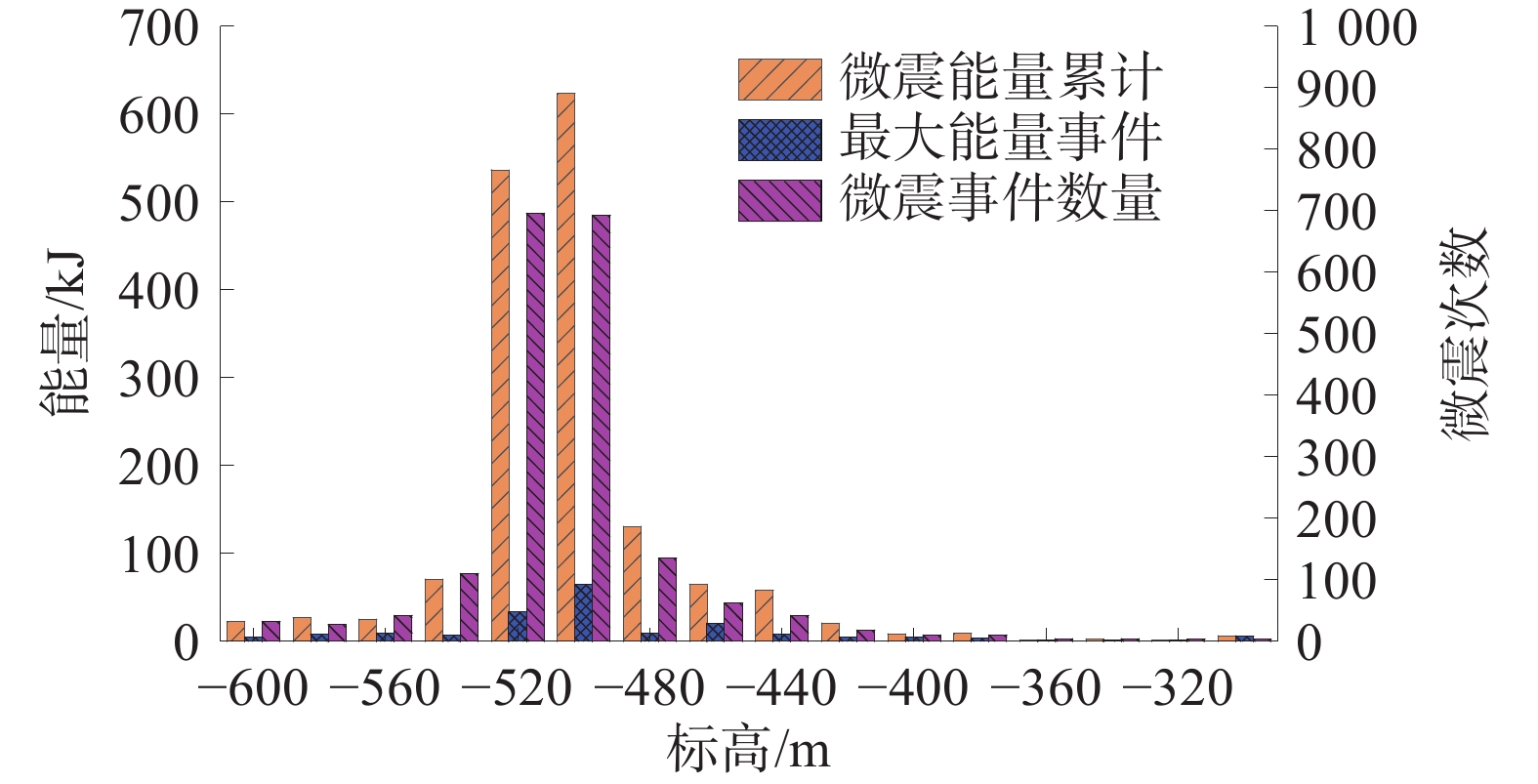
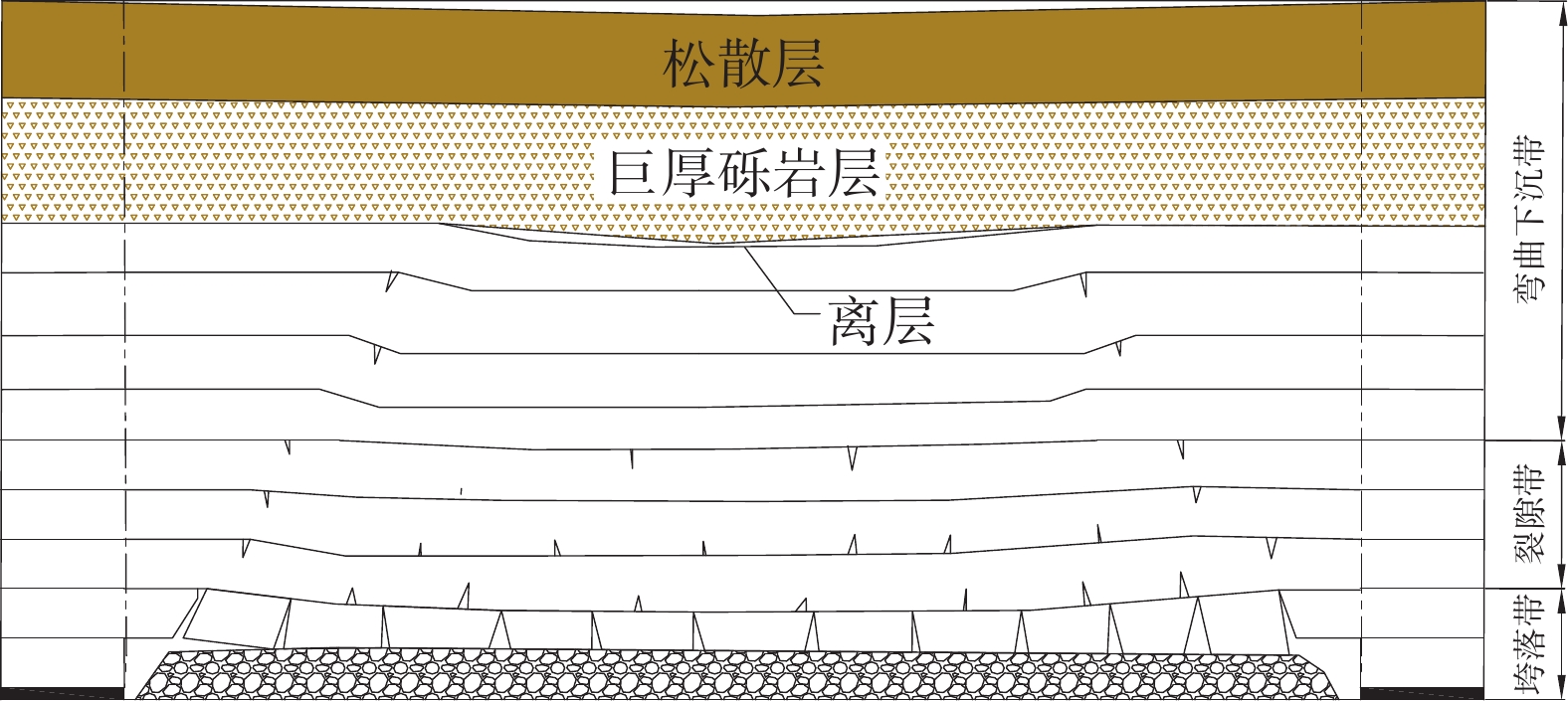
3上1111工作面位于SOS微震监测系统监测范围，工作面周围布置了5个微震探头。微震事件分布如图2所示，微震事件在标高上的分布特征如图3所示，工作面开采后覆岩结构如图4所示。
![]()
图 3 各标高微震事件分布特征Figure 3. Distribution characteristics of micro-seismic events at each level由图2可知：微震事件集中分布在靠近3上1109采空区一侧，并沿走向逐渐向扩散至整个工作面，大部分微震事件分布在工作面前方300 m范围，沿倾向方向微震事件最远分布在两巷道外侧约60 m范围。
由图3可知：工作面顶板微震事件多分布在−440 m标高以下岩层，103 J及以上能量事件集中分布在−460 m标高以下岩层，工作面各标高范围内微震能量累计、微震事件数量、最大能量事件变化趋势相似，在标高−500~−460 m范围内均处于峰值区。工作面采动上覆岩层竖向破坏特征从下至上破坏程度呈逐渐减弱，依次形成垮落带、裂隙带、弯曲下沉带，微震事件震源能量可以表征岩层损伤破坏程度。因此，根据微震事件在垂直方向上的分布特征判断，工作面开采后裂隙带发育高度上限在−460 m标高左右，即距离顶板高度80 m附近岩层。
由图4可以看出，3上1111工作面巨厚砾岩层位于开采后覆岩“三带”中的弯曲下沉带，破坏程度较小，与松散层相邻，为控制松散层移动的关键层。离层最容易发生在关键层与下覆岩层的界面处[22]，覆岩的破坏与移动与其自身物理力学性质具有密切联系，高位砾岩层因厚度、强度与其下岩层明显差异引发离层。
3. 高位巨厚砾岩层变形及地表沉降控制机理
3.1 巨厚砾岩层Euler-Bernoulli裂缝梁结构模型
研究表明[23-25]，工作面开采后采空区顶板岩体经过垮落、裂隙延展等过程，在自重应力的作用下逐渐趋于平衡状态，此区域岩体破坏最为严重，整体弯曲下沉量最大，上覆岩层裂隙走向断面上逐渐形成梯形结构，硬厚岩层的存在屏蔽了梯形结构的纵向发育，离层最终转移至主关键层底部。高位巨厚砾岩层作为松散层关键层，对覆岩破坏、下沉向上传递具有一定的控制作用。
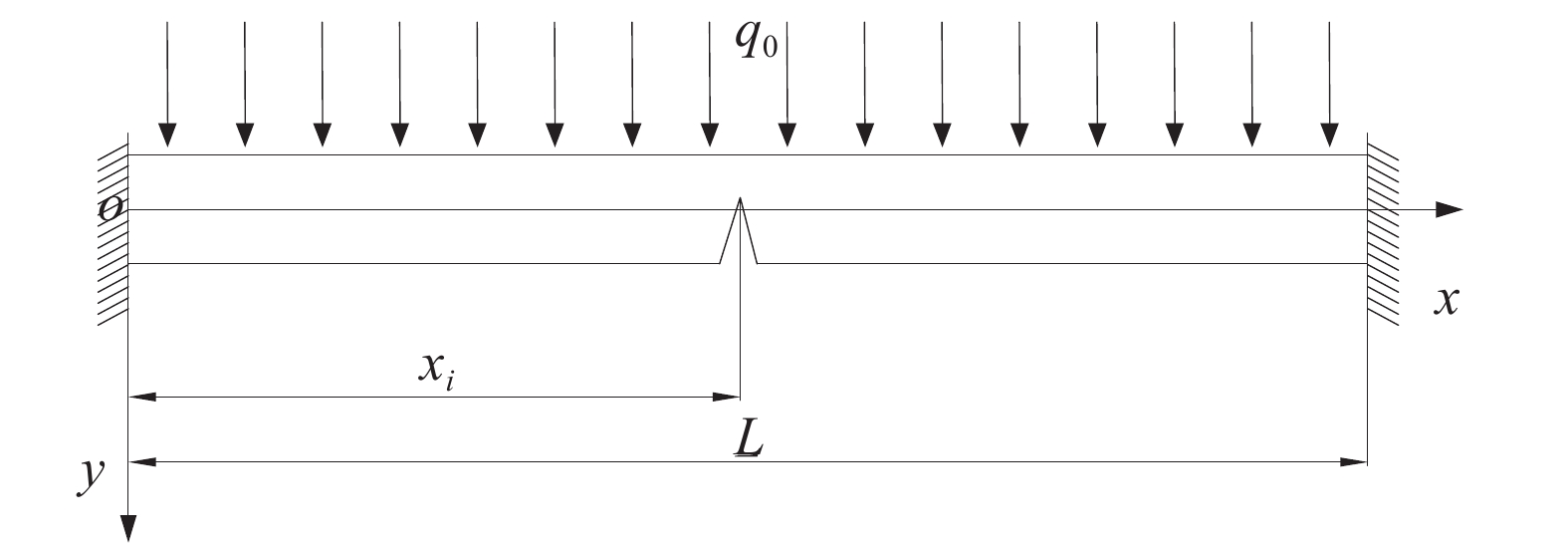
巨厚砾岩层位于工作面基岩顶部，距离工作面较远，基岩破坏区范围呈梯形向上减小，距离工作面越远受采动影响小，并且巨厚砾岩厚达100 m、强度较大，其破坏程度小。西十一采区工作面开采形成采空区高位巨厚砾岩层厚度与倾向长度差别较小，走向较长，可将工作面开采后高位巨厚砾岩层视为下侧具有裂缝的Euler-Bernoulli 固支裂缝梁结构力学模型（图5）。
![]()
图 5 Euler-Bernoulli 固支裂缝梁结构力学模型q0—岩层上覆载荷；L—砾岩层走向悬空长度；xi—裂缝位置。Figure 5. Euler-Bernoulli structural mechanics model for fixed supported cracked beam文献[26]将裂缝视为单向旋转弹簧机构，下面介绍Euler-Bernoulli 固支裂缝梁的挠度控制方程推导过程。
单向旋转弹簧在力偶M作用下可任意旋转，弹性刚度为K，当力偶M>M0，M0为裂纹闭合时的临界力偶，旋转弹簧转角与力偶无关，保持常量。单向旋转弹簧的本构方程为：
$$ \theta {\text{ = }}\frac{M}{K} - \frac{{M - {M_0}}}{K}H(M - {M_0}) $$ (1) 式中：θ为弹簧的转角；H(x)为Heaviside函数，令x=M-M0，M>M0时H(M−M0)=1，M=M0时H(M−M0)=1/2，M<M0时H(M−M0)=0。
假设梁的抗弯刚度为(EI)0，当旋转弹簧转角为θ0=M0/K时，裂缝闭合，梁变为无裂缝的完整梁。梁的转角ϕ为：
$$\begin{split} &\begin{gathered} \phi = - \frac{M}{{{{(EI)}_0}}}x - \frac{M}{K}\left[ - \frac{{{M_0}}}{M} + \left(1 + \frac{{{M_0}}}{M}\right)H(M + {M_0})\right]\cdot \\ H(x - {x_0})\end{gathered}\\[-16pt]& \end{split} $$ (2) 假设下侧开闭裂缝的梁的等效刚度为(EI)e。
$$ M = - {(EI)_{\mathrm{e}}}\frac{{{\mathrm{d}}\phi }}{{{\mathrm{d}}x}} $$ (3) 根据式（2）、式（3）得到梁的等效抗弯刚度为：
$$ \frac{1}{{{{(EI)}_{\mathrm{e}}}}} = \frac{1}{{{{(EI)}_0}}} + \frac{\alpha }{K}\delta (x - {x_0}) $$ (4) 式中：δ(x)为Delta函数，定义为δ(x)=d(H(x))/dx。 α记为：
$$ \alpha = - \frac{{{M_0}}}{M} + \left[1 + \frac{{{M_0}}}{M}\right]H(M + {M_0}) $$ (5) 假设Euler-Bernoulli 固支裂缝梁承受横向载荷q(x)，在梁的x=xi(i=1，2，3，4，···，N)处底部存在开闭裂缝，裂缝i的等效单向旋转弹簧的刚度为Ki，则梁的等效抗弯刚度(EI)e为：
$$ \frac{1}{{{{(EI)}_{\mathrm{e}}}}} = \frac{1}{{{{(EI)}_0}}} + \sum\limits_{i = 1}^N {\frac{{{\alpha _i}}}{{{K_i}}}} \delta (x - {x_i}) $$ (6) $$ {\alpha _i} = - \frac{{{M_{i0}}}}{{{M_i}}} + \left[1 + \frac{{{M_{i0}}}}{{{M_i}}}\right]H({M_i} + {M_{i0}}) $$ (7) 式中：Mi为裂缝i的弯矩；Mi0为裂缝i的闭合临界弯矩；N为裂缝总数；Ki为裂缝i的等效单向旋转弹簧刚度；αi为裂缝i的α值。
则梁的弯曲挠度w(x)控制方程以及横截面弯矩M和剪力Fs分别为：
$$\begin{split} &\begin{gathered} \frac{{{{{\mathrm{d}}}^2}}}{{{{\mathrm{d}}}{x^2}}}\left[{(EI)_{\mathrm{e}}}\frac{{{{{\mathrm{d}}}^2}w}}{{{{\mathrm{d}}}{x^2}}}\right] = q(x) \\ M = - {(EI)_{\mathrm{e}}}\frac{{{{{\mathrm{d}}}^2}w}}{{{{\mathrm{d}}}{x^2}}} \\ {F_{\mathrm{s}}} = - \frac{{{\mathrm{d}}}}{{{{\mathrm{d}}}x}}\left[{(EI)_{\mathrm{e}}}\frac{{{{{\mathrm{d}}}^2}w}}{{{{\mathrm{d}}}{x^2}}}\right] \end{gathered}\\[-16pt]& \end{split}$$ (8) 引入以下无量纲参数：
$$ \left\{ \begin{gathered} \zeta = \frac{x}{L},{\zeta _i} = \frac{{{x_i}}}{L} \\ W(\zeta ) = \frac{{\omega (x)}}{L},Q(\zeta ) = \frac{{q(x){L^3}}}{{{{(EI)}_0}}} \\ {k_i} = \frac{{L{K_i}}}{{{{(EI)}_0}}},{(\overline {EI} )_{\mathrm{e}}} = \frac{{{{(EI)}_{\mathrm{e}}}}}{{{{(EI)}_0}}} \\ \end{gathered} \right. $$ (9) 则无量纲等效抗弯刚度为：
$$ \frac{1}{{{{(\overline {EI} )}_{\mathrm{e}}}}} = 1 + \sum\limits_{i = 1}^N {\frac{{{\alpha _i}}}{{{K_i}}}} \delta (\zeta - {\zeta _i}) $$ (10) 式中：αi为式（11），记式（11）中mi=MiL/(EI)0，mi0=Mi0L/(EI)0。
$$ {\alpha _i} = - \frac{{{m_{i0}}}}{{{m_i}}} + \left[1 + \frac{{{m_{i0}}}}{{{m_i}}}\right]H({m_i} + {m_{i0}}) $$ (11) 将无量纲参数代入式（8）得到挠度控制方程的无量纲形式，积分得到挠度控制方程为：
$$ \begin{split} &\begin{gathered} W(\zeta ) = {Q^{[4]}}(\zeta ) + \sum\limits_{i = 1}^N {\frac{{{\alpha _i}}}{{{k_i}}}{Q^{[2]}}({\zeta _i})H(\zeta - {\zeta _i})} + \\ {C_1}\left[\frac{{{\zeta ^3}}}{6} + \sum\limits_{i = 1}^N {\frac{{{\alpha _i}}}{{{k_i}}}{\zeta _i}(\zeta - {\zeta _i})H(\zeta - {\zeta _i})} \right] + \\ {C_2}\left[\frac{{{\zeta ^2}}}{2} + \sum\limits_{i = 1}^N {\frac{{{\alpha _i}}}{{{k_i}}}(\zeta - {\zeta _i})H(\zeta - {\zeta _i})} \right] + \\ {C_3}\zeta + {C_4} \end{gathered}\\[-16pt]& \end{split}$$ (12) 式中：Ci（i=1,2,3,4）为待定系数，可由梁的4个边界确定，Q[1](ζ)、Q[2](ζ)、Q[3](ζ)、Q[4](ζ)为Q(ζ)的积分，见式（13）：
$$ \begin{gathered} {Q^{[1]}}(\zeta ) = \int_0^\zeta {Q(\zeta ){\rm{d}}\zeta } \\ {Q^{[2]}}(\zeta ) = \int_0^\zeta {\int_0^\zeta {Q(\zeta ){\rm{d}}\zeta } } {\rm{d}}\zeta \\ {Q^{[3]}}(\zeta ) = \int_0^\zeta {\int_0^\zeta {\int_0^\zeta {Q(\zeta ){\rm{d}}\zeta } } {\rm{d}}\zeta } {\rm{d}}\zeta \\ {Q^{[4]}}(\zeta ) = \int_0^\zeta {\int_0^\zeta {\int_0^\zeta {\int_0^\zeta {Q(\zeta ){\rm{d}}\zeta } } {\rm{d}}\zeta } {\rm{d}}\zeta } \\ \end{gathered} $$ (13) 梁截面的无量纲弯矩m(ξ)和剪力fs(ξ)分别为：
$$ \begin{array}{l}m(\xi )\text=\dfrac{M(x）L}{{(EI)}_{0}}=-[{Q}^{[2]}(\xi )+{C}_{1}\xi +{C}_{2}]\\ {f}_{s}(\xi )=\dfrac{{F}_{s}(x）{L}^{2}}{{(EI)}_{0}}=-[{Q}^{[1]}(\xi )+{C}_{1}]\end{array} $$ (14) 3.2 高位巨厚砾岩层对地表沉降控制机理
采空区高位巨厚砾岩层简化为Euler-Bernoulli固支梁，则边界条件为：
$$ W(\zeta ) = \frac{{\mathrm{d}}}{{{\mathrm{d}}x}}W(\zeta ) = 0,\zeta = 0,1 $$ (15) 梁上的横向载荷无量纲形式为：
$$ {Q_0} = {q_0}{L^3}/{(EI)_0} $$ (16) 式中：q0为岩层上覆载荷。
假设巨厚砾岩层裂缝i的深度为di，梁的厚度为h，则裂缝的无量纲刚度ki为：
$$ {k_i} = \frac{L}{h} \cdot \frac{{0.9{{[({d_i}/h) - 1]}^2}}}{{({d_i}/h)[2 - ({d_i}/h)]}} $$ (17) 结合以上参数，可求得固支裂缝梁的挠度控制方程。研究表明[27]，裂缝越靠近梁跨中，裂缝梁挠度峰值和转角峰值便越大，弹性地基梁反力参数较小时，随着裂缝个数的增加，挠度逐渐增大。对于巨厚砾岩层裂缝固支梁，其作为主关键层，底部易产生离层空间，底部反力较弱。因此，其挠度受裂缝数量以及位置控制。地表沉降是由于其下岩层的弯曲变形引起，高位巨厚砾岩裂缝固支梁最大挠度直接影响地表沉降量，高位巨厚砾岩受采动影响小，破坏程度低，裂缝数量较少，其破坏程度对地表沉降具有控制作用。
4. 覆岩移动规律数值模拟
4.1 数值模拟模型
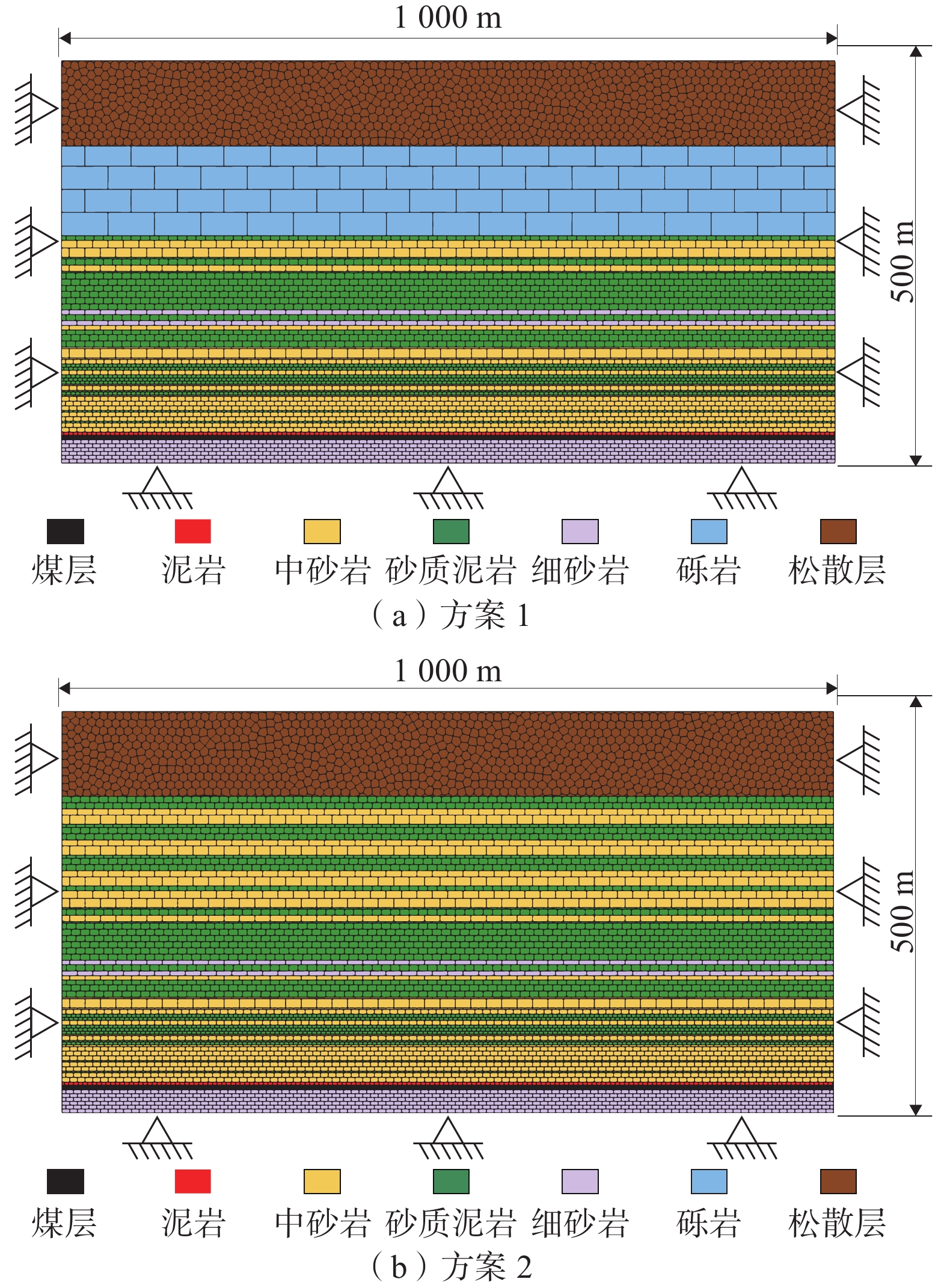
以3上1103工作面开采及覆岩条件为背景，采用UDEC离散元方法数值模拟软件研究高位巨厚砾岩层工作面覆岩移动规律，取沿工作面走向的剖面建立模型，参照钻孔2006-1建立模型地层，松散层采用Voronoi随机节理划分。为验证巨厚砾岩层对地表沉降的控制作用，按照巨厚砾岩层下方岩层组成结构，将其用20 m厚砂质泥岩和中砂岩交互重复地层取代建立数值模型（图6）。
模型尺寸1 000 m×520 m，模型左右边界、底部边界施加法向约束，顶部为自由边界，考虑边界效应的影响，模型左右边界各留250 m，工作面走向长度500 m，采高6 m，每25 m开挖1次，采用Mohr-coulomb本构模型，岩层力学性质参数见表4。
表 4 各岩层力学参数Table 4. Mechanical parameters of each rock formation地层 密度/
(kg·m−3)体积模量/
GPa剪切模量/
GPa内摩擦角/
（º）黏聚力/
MPa抗拉强度/
MPa煤层 1300 1.56 0.64 32 3.29 0.94 泥岩 2540 3.03 1.56 34 3.59 1.02 中砂岩 2560 6.34 2.59 30 8.97 4.82 砂质泥岩 2795 3.88 1.79 40 4.85 2.62 细砂岩 2600 8.10 4.86 39 5.45 3.53 砾岩 2715 9.80 8.62 30 13.50 3.59 松散层 2000 0.28 0.09 25 0.85 0.35 4.2 数值模拟结果
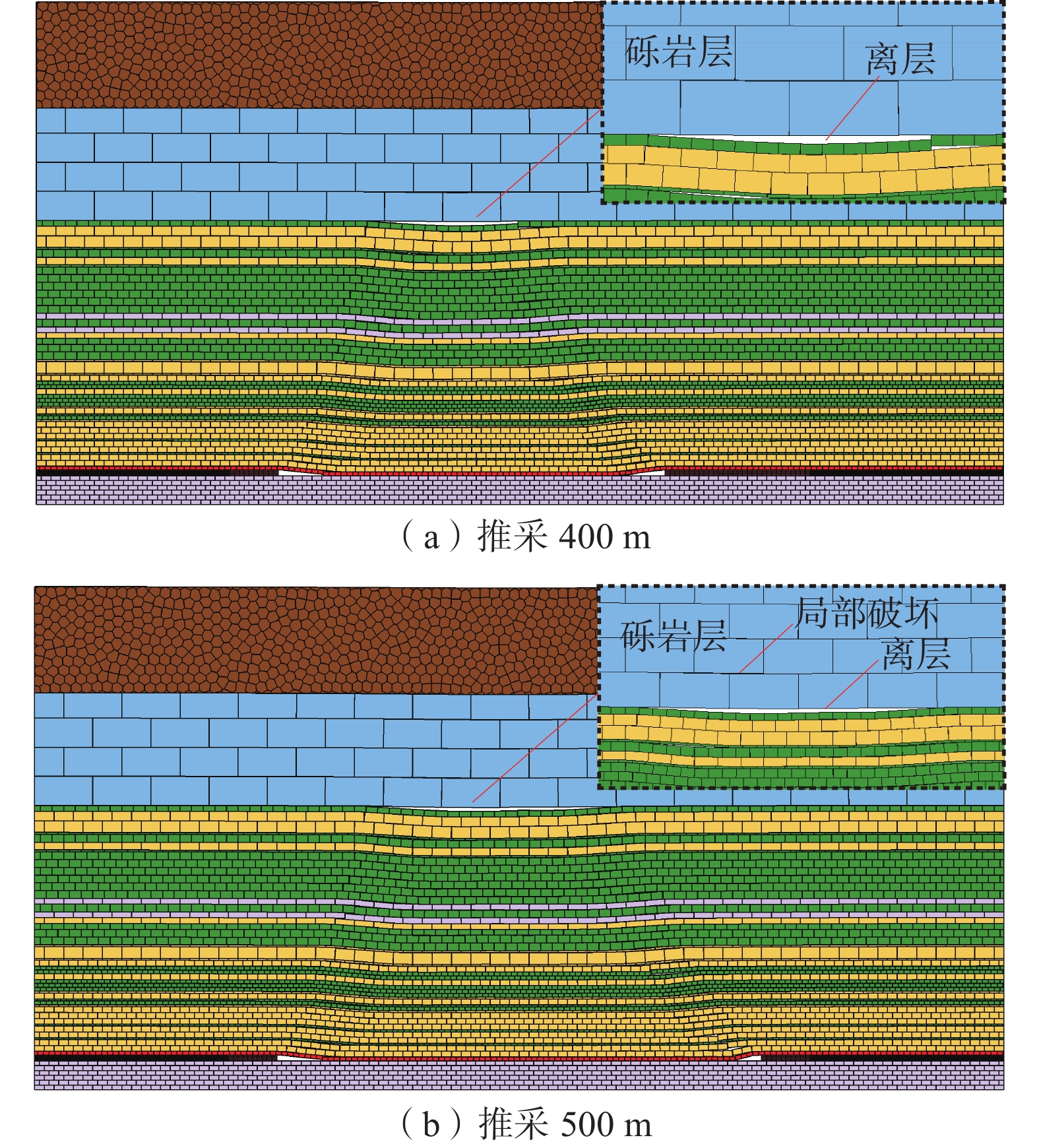
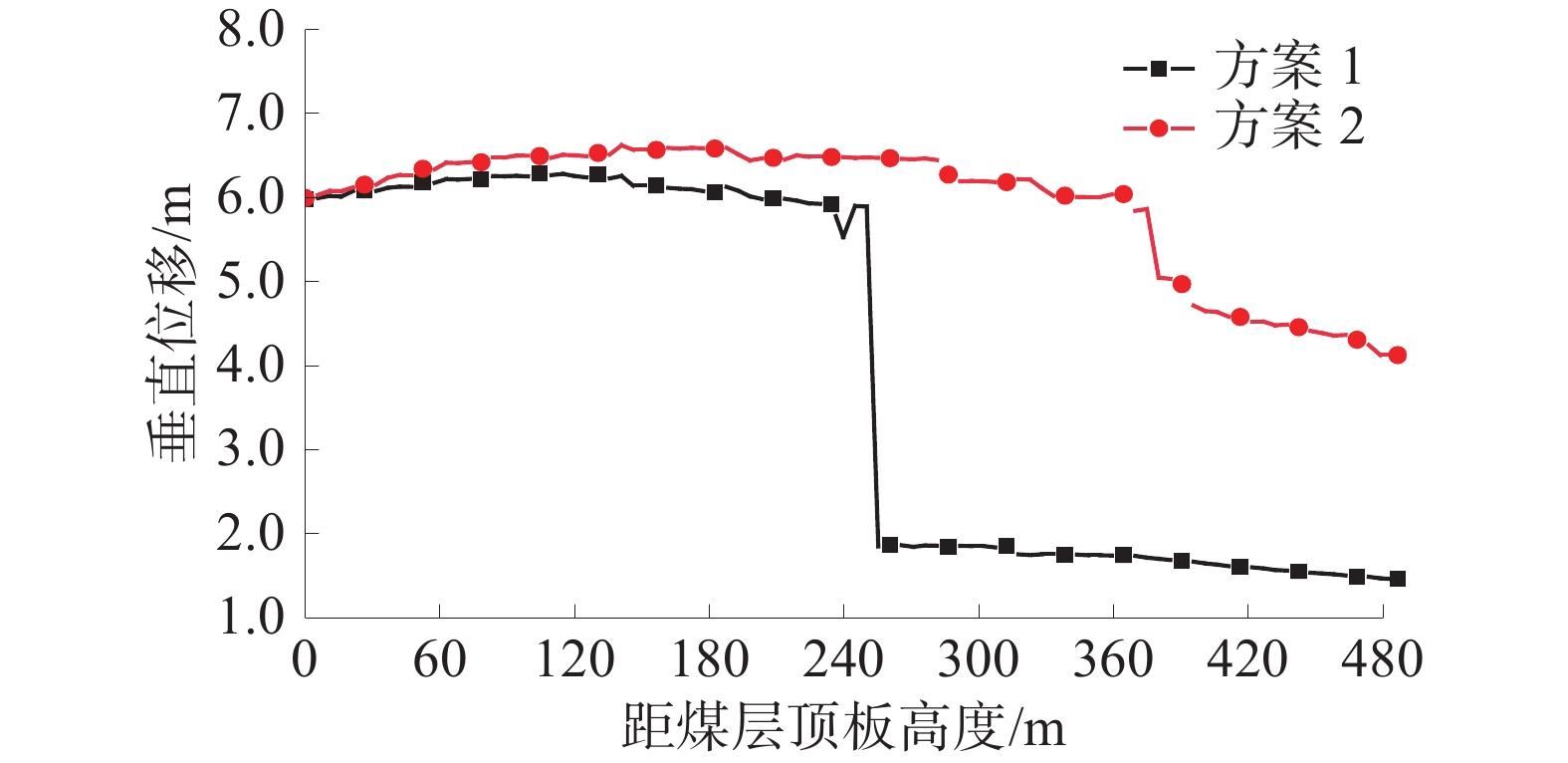
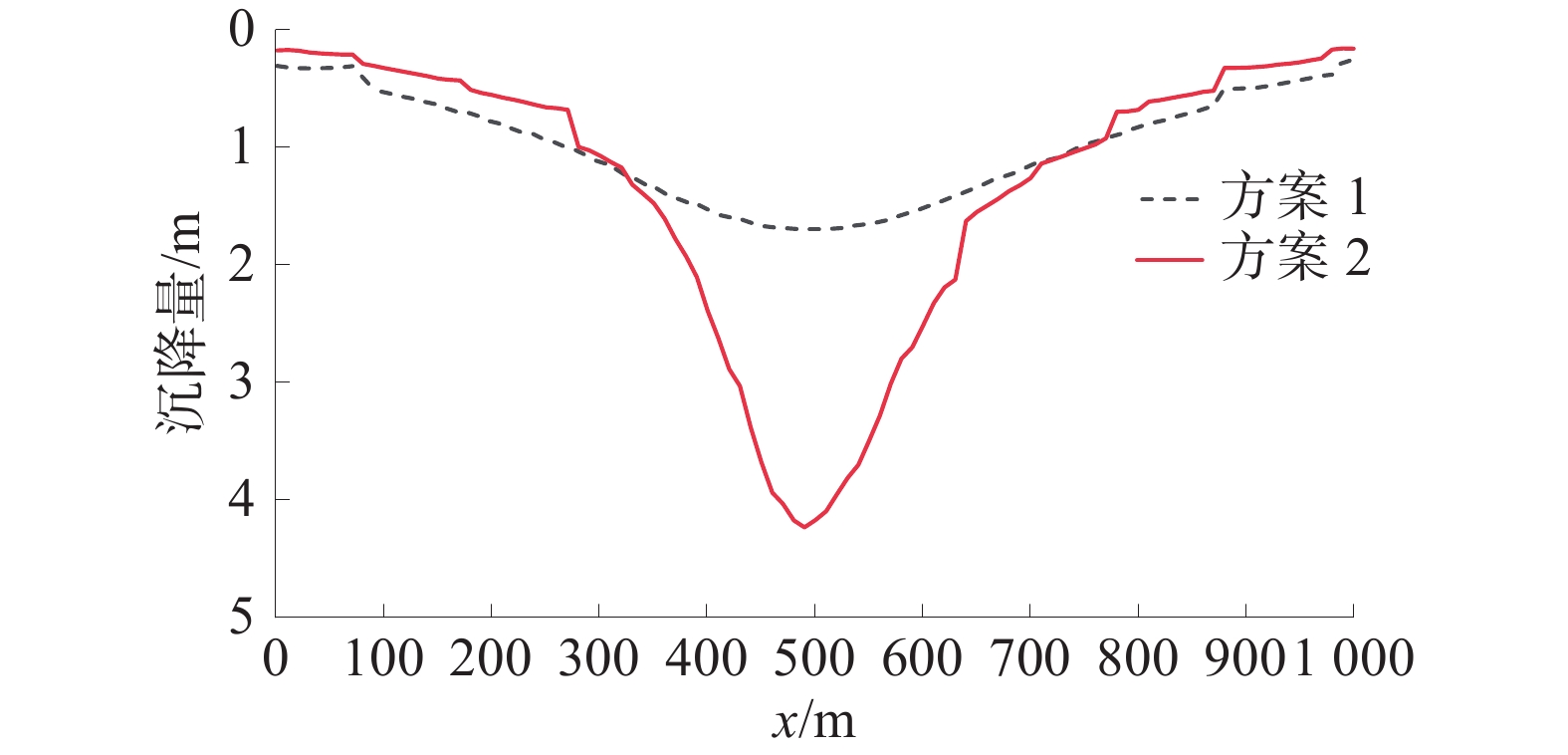
工作面推采400、500 m覆岩破坏情况如图7所示，方案1、方案2工作面走向中部覆岩垂直位移曲线如图8所示，方案1、方案2地表沉降曲线如图9所示。
![]()
图 7 巨厚砾岩底部离层演化过程Figure 7. Separated layer evolution in the base of huge-thick conglomerate由图7可知：当工作面推采至400 m时，裂隙发育至巨厚砾岩层相邻岩层，巨厚砾岩层与底部岩层离层，离层空间呈“月牙”形，随着工作面推进，离层空间逐渐增加，逐渐演变为“盘”形，砾岩层底部逐渐产生局部破坏裂隙，变形不断增加，但整体依旧具有承载能力，裂隙未贯穿整个岩层。
由图8可知：方案1上覆岩层垂直位移均呈阶梯式变化，位移变化节点在距煤层260 m附近范围出现阶梯式下降；而方案2上覆岩层垂直位移呈现缓慢下降，松散层与基岩交界区域呈陡坡式下降。
由图9可知：方案2地表沉降最大值远大于方案1。
数值模拟结果显示，巨厚砾岩层与底部岩层相比，其抵抗变形的能力更高，易发生离层，随着采空区跨度增加到一定程度，砾岩层中间底部产生局部破坏，离层空间经历了“月牙”形、“盘”形的变化形态。2种模拟方案工作面走向中部覆岩垂直位移、地表沉降呈现出明显差异，方案1在高位巨厚砾岩底部边界区域覆岩垂直位移呈现出阶梯式下降，方案2则为缓慢下降，方案1地表沉降量远小于方案2，高位巨厚砾岩层对地表沉降具有明显控制作用。
5. 地表沉降实测
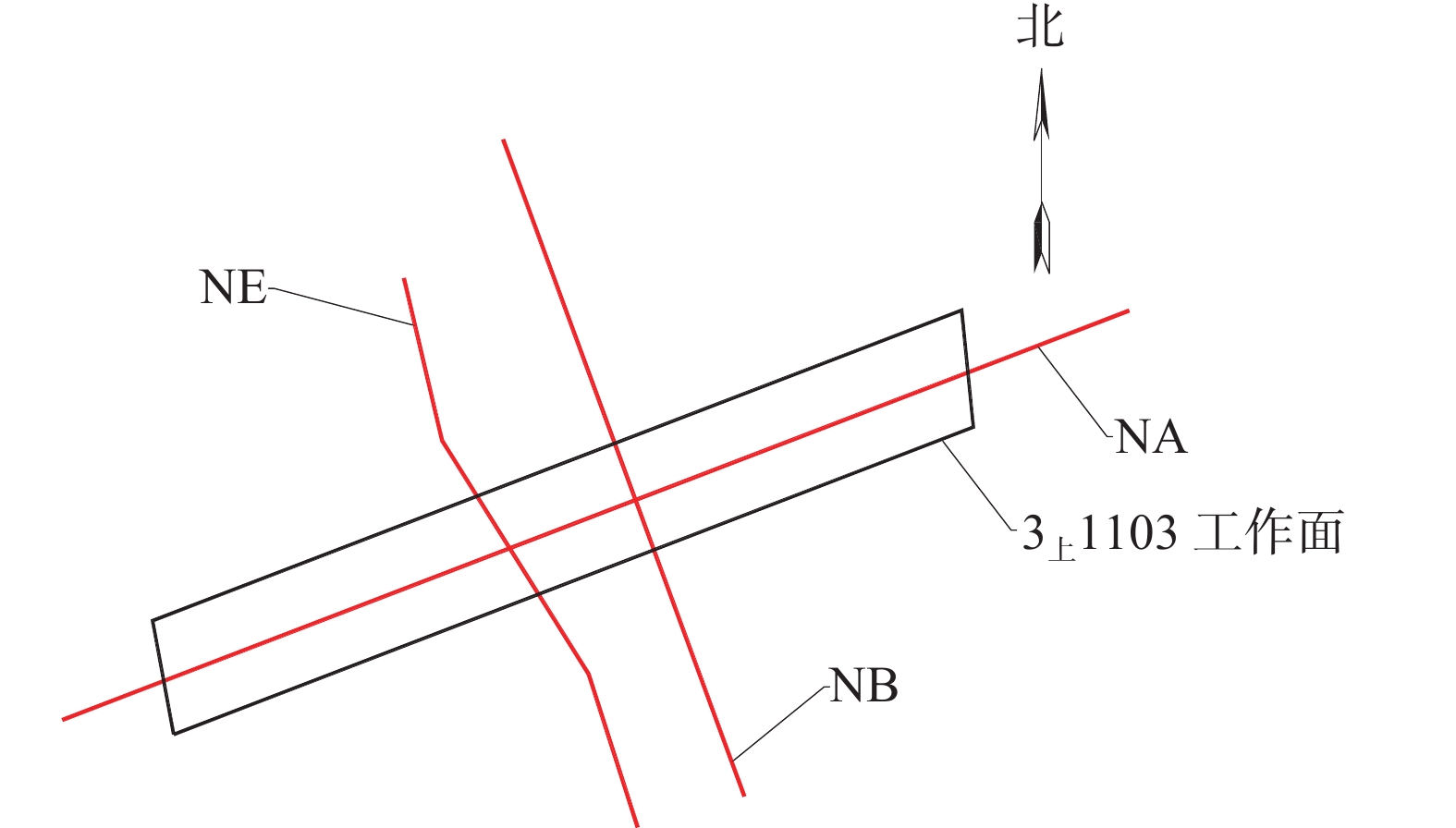
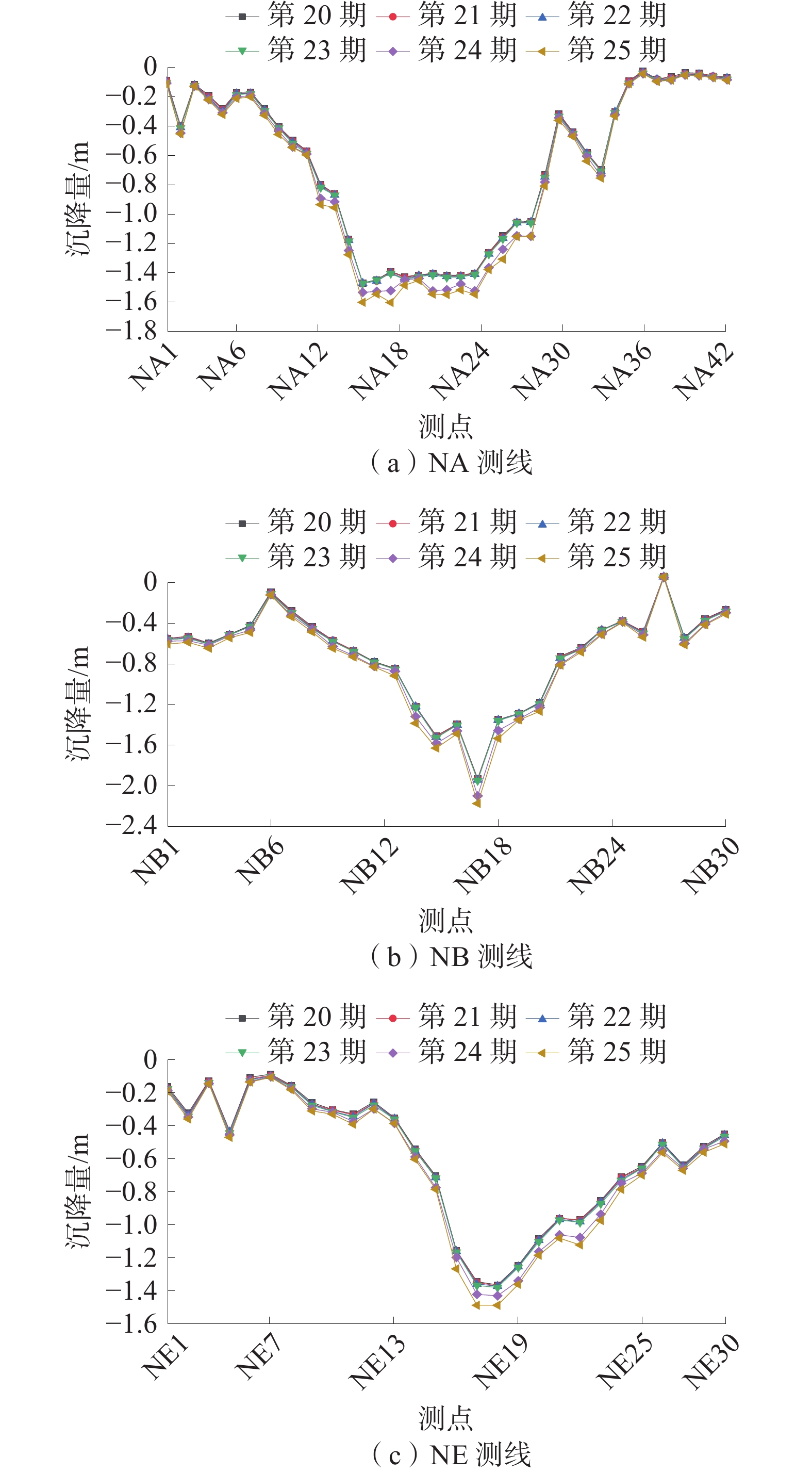
3上1103工作面开采期间开展了地表岩移观测，在工作面中间沿走向布置了NA测线，沿工作面倾向分布布置了NE、NB测线，测点间距50 m，开展了25次高程观测，观测周期从开采起至停采覆岩稳定如图10所示，3上1103工作面地表各测线20~25期沉降曲线如图11所示。
由观测成果可知：NA测线观测最大下沉点为那NA17号点，最大下沉值为1.602 m；NB测线观测最大下沉点为NB16号点，最大下沉值为2.175 m；NE测线观测最大下沉点为NE18号点，最大下沉值为1.488 m。工作面地表下沉系数0.38，明显低于充分采动下的地表下沉系数，地表非充分采动。根据文献[28]，西十一采区东翼南部西五采区东翼3上510工作面位于砾岩层尖灭区，其实测地表最大沉降量3.45 m，明显大于高位存在巨厚砾岩层的3上1103地表最大沉降量。
工作面地表沉降量实测结果显示，高位巨厚砾岩区工作面地表处于非充分采动状态，沉降量明显低于巨厚砾岩层尖灭区近似条件工作面开采引起的地表沉降。高位巨厚砾岩层开采后地表沉降具有明显的控制作用。
6. 结 语
1）基于微震监测数据分析，工作面开采后裂隙带发育高度上限在距离顶板高度80 m附近岩层，高位巨厚砾岩层位于顶板弯曲下沉带范围，受采动影响下，破坏裂隙发育程度低。
2）建立了巨厚砾岩层Euler-Bernoulli 固支裂缝梁力学模型，推导了裂缝影响下梁的挠度控制方程，阐明了巨厚砾岩层对地表沉降的控制机理。地表沉降是由于其下岩层的弯曲变形引起，高位巨厚砾岩裂缝固支梁最大挠度直接影响地表沉降量，高位巨厚砾岩破坏程度由裂缝数量、裂缝位置控制，巨厚砾岩层处于高位，受工作面采动影响有限，高位巨厚砾岩破坏程度低，巨厚砾岩裂缝的发育对地表沉降具有控制作用。
3）数值模拟结果显示，巨厚砾岩层底部易发生离层，离层空间经历了“月牙”形、“盘”形的变化形态。2种方案工作面走向中部覆岩垂直位移、地表沉降呈现出明显差异，方案1在高位巨厚砾岩底部边界区域覆岩垂直位移呈现出阶梯式下降，方案2则为缓慢下降，方案1地表沉降量远小于方案2，高位巨厚砾岩层对地表沉降具有明显控制作用。根据实测地表沉降量结果显示，高位巨厚砾岩层工作面开采地表处于非充分采动状态，沉降量要远小于砾岩层尖灭区近似条件下工作面开采引起的沉降量。
-
![]()
图 3 各标高微震事件分布特征
Figure 3. Distribution characteristics of micro-seismic events at each level
![]()
图 5 Euler-Bernoulli 固支裂缝梁结构力学模型
q0—岩层上覆载荷；L—砾岩层走向悬空长度；xi—裂缝位置。
Figure 5. Euler-Bernoulli structural mechanics model for fixed supported cracked beam
![]()
图 7 巨厚砾岩底部离层演化过程
Figure 7. Separated layer evolution in the base of huge-thick conglomerate
表 1 12-16钻孔顶板地层统计表
Table 1 Stratigraphic statistics for roof of drill hole 12-16
序号 岩性 厚度/m 序号 岩性 厚度/m 53 松散层 89.00 27 粗砂岩 5.37 52 粉砂岩 63.45 26 泥岩 2.28 51 砾岩 2.75 25 粉砂岩 1.90 50 泥岩 12.90 24 粗砂岩 6.85 49 砾岩 194.90 23 粉砂岩 8.27 48 泥岩 2.90 22 中砂岩 0.76 47 细砂岩 1.57 21 粉砂岩 1.62 46 泥岩 0.76 20 中砂岩 1.71 45 细砂岩 0.76 19 泥岩 6.37 44 泥岩 9.61 18 细砂岩 1.28 43 粉砂岩 6.90 17 粉砂岩 2.19 42 泥岩 7.94 16 中砂岩 2.95 41 细砂岩 1.33 15 泥岩 1.88 40 泥岩 3.42 14 粉砂岩 4.23 39 中砂岩 3.90 13 细砂岩 1.81 38 泥岩 9.61 12 粉砂岩 2.90 37 细砂岩 0.57 11 泥岩 4.95 36 泥岩 5.47 10 粉砂岩 3.52 35 细砂岩 6.23 9 细砂岩 0.86 34 煤层 0.19 8 粉砂岩 3.80 33 泥岩 5.99 7 细砂岩 1.05 32 煤层 0.32 6 泥岩 4.57 31 泥岩 2.91 4 粉砂岩 3.42 30 粉砂岩 5.94 3 细砂岩 1.66 29 泥岩 21.40 2 中砂岩 10.93 28 粉砂岩 3.52 1 3上煤层 3.98 
下载: 导出CSV
表 2 2006-2钻孔顶板地层统计表
Table 2 Stratigraphic statistics for roof of drill hole 2006-2
序号 岩性 厚度/m 序号 岩性 厚度/m 27 松散层 104.45 13 中砂岩 7.25 26 砾岩层 175.50 12 砂质泥岩 13.60 25 砂质泥岩 10.20 11 中砂岩 20.65 24 中砂岩 22.15 10 砂质泥岩 9.85 23 砂质泥岩 1.40 9 中砂岩 5.95 22 细砂岩 8.40 8 砂质泥岩 7.40 21 中砂岩 12.85 7 中砂岩 3.85 20 砂质泥岩 28.95 6 砂质泥岩 5.00 19 中砂岩 5.40 5 中砂岩 3.20 18 砂质泥岩 2.65 4 砂质泥岩 4.00 17 煤 0.35 3 中砂岩 7.65 16 砂质泥岩 15.20 2 泥岩 1.20 15 细砂岩 7.30 1 3上煤层 5.50 14 砂质泥岩 13.45
下载: 导出CSV
表 3 2006-1钻孔顶板地层统计表
Table 3 Stratigraphic statistics for roof of drill hole 2006-1
序号 岩性 厚度/m 序号 岩性 厚度/m 31 松散层 110.65 15 中砂岩 8.00 30 砾岩 115.80 14 砂质泥岩 7.70 29 砂质泥岩 5.35 13 中砂岩 6.50 28 中砂岩 21.50 12 砂质泥岩 12.65 27 砂质泥岩 8.60 11 中砂岩 7.85 26 中砂岩 8.85 10 砂质泥岩 6.15 25 砂质泥岩 50.35 9 中砂岩 20.10 24 煤 0.35 8 砂质泥岩 1.95 23 砂质泥岩 0.75 7 中砂岩 4.55 22 细砂岩 4.95 6 砂质泥岩 0.65 21 砂质泥岩 9.05 5 中砂岩 5.00 20 细砂岩 5.65 4 砂质泥岩 0.95 19 中砂岩 5.85 3 中砂岩 11.80 18 砂质泥岩 22.45 2 泥岩 2.45 17 中砂岩 14.05 1 3上煤层 6.40 16 砂质泥岩 0.45
下载: 导出CSV
表 4 各岩层力学参数
Table 4 Mechanical parameters of each rock formation
地层 密度/
(kg·m−3)体积模量/
GPa剪切模量/
GPa内摩擦角/
（º）黏聚力/
MPa抗拉强度/
MPa煤层 1300 1.56 0.64 32 3.29 0.94 泥岩 2540 3.03 1.56 34 3.59 1.02 中砂岩 2560 6.34 2.59 30 8.97 4.82 砂质泥岩 2795 3.88 1.79 40 4.85 2.62 细砂岩 2600 8.10 4.86 39 5.45 3.53 砾岩 2715 9.80 8.62 30 13.50 3.59 松散层 2000 0.28 0.09 25 0.85 0.35
下载: 导出CSV
-
[1] 郭广礼,王悦汉,马占国. 煤矿开采沉陷有效控制的新途径[J]. 中国矿业大学学报,2004(2):150−153. GUO Guangli, WANG Yuehan, MA Zhanguo. A new method for ground subsidence control in coal mining[J]. Journal of China University of Mining & Technology, 2004(2): 150−153.
[2] 郭广礼,李怀展,查剑锋,等. 平原煤粮主产复合区煤矿开采和耕地保护协同发展研究现状及对策[J]. 煤炭科学技术,2023,51(1):416−426. GUO Guangli, LI Huaizhan, ZHA Jianfeng, et al. Research status and countermeasures of coordinated development of coal mining and cultivated land protection in the plain coal-cropland overlapped areas[J]. Coal Science and Technology, 2023, 51(1): 416−426.
[3] 黄平路,陈从新,肖国峰,等. 复杂地质条件下矿山地下开采地表变形规律的研究[J]. 岩土力学,2009,30(10):3020−3024. HUANG Pinglu, CHEN Congxin, XIAO Guofeng, et al. Study of rock movement caused by underground mining in mines with complicated geological conditions[J]. Rock and Soil Mechanics, 2009, 30(10): 3020−3024.
[4] 樊占文,郭永红,杨可明. 煤矿开采地表移动与变形规律常规化研究模式[J]. 煤炭科学技术,2014,42(S1):252−255. FAN Zhanwen, GUO Yonghong, YANG Keming. Routinized studying mode on land surface movement and deformation law of mining subsidence in coal mine[J]. Coal Science and Technology, 2014, 42(S1): 252−255.
[5] 许家林,钱鸣高. 关键层运动对覆岩及地表移动影响的研究[J]. 煤炭学报,2000(2):122−126. XU Jialin, QIAN Minggao. Study on the influence of key strata movement on subsidence[J]. Journal of China Coal Society, 2000(2): 122−126.
[6] 王家臣,许家林,杨胜利,等. 煤矿采场岩层运动与控制研究进展−纪念钱鸣高院士“砌体梁”理论40年[J]. 煤炭科学技术,2023,51(1):80−94. WANG Jiachen, XU Jialin, YANG Shengli, et al. Development of strata movement and its control in underground mining: ln memory of 40 years of Voussoir Beam Theory proposed by Academician Minggao Qian[J]. Coal Science and Technology, 2023, 51(1): 80−94.
[7] 许家林,钱鸣高,朱卫兵. 覆岩主关键层对地表下沉动态的影响研究[J]. 岩石力学与工程学报,2005(5):787−791. XU Jialin, QIAN Minggao, ZHU Weibing. Study on influences of primary key stratum on surface dynamic subsidence[J]. Chinese Journal of Rock Mechanics and Engineering, 2005(5): 787−791.
[8] 张广超,曲治,孟祥军,等. 远场高位厚硬岩层破断运动机理及响应规律研究[J]. 煤炭科学技术,2023(11):12−22. ZHANG Guangchao, QU Zhi, MENG Xiangjun, et al. Study on the mechanism and response law of fracture movement on the super-highposition hard-and-hick strata[J]. Coal Science and Technology, 2023(11): 12−22.
[9] 王跃宗,郭广礼,李怀展,等. 坚硬顶板浅埋煤层开采地表移动特征[J]. 中国科技论文,2022,17(9):1021−1026. WANG Yuezong, GUO Guangli, LI Huaizhan, et al. Surface movement characteristics of shallow coal seam mining under hard roof[J]. China Sciencepaper, 2022, 17(9): 1021−1026.
[10] 孙庆先,陈清通,李宏杰,等. 关键层破断对地表移动变形超前影响的机理研究[J]. 煤炭工程,2023,55(2):105−109. SUN Qingxian, CHEN Qingtong, LI Hongjie, et al. Advance influence mechanism of key strata rupture on surface movement[J]. Coal Engineering, 2023, 55(2): 105−109.
[11] 柴敬,雷武林,李昊,等. 三维物理模型模拟深部巨厚砾岩下综放开采地表移动[J]. 西安科技大学学报,2020,40(2):204−211. CHAI Jing, LEI Wulin, LI Hao, et al. Simulate of the surface movement of fully-mechanized caving mining under the deep thick conglomerate using 3D physical model[J]. Journal of Xi’an University of Science and Technology, 2020, 40(2): 204−211.
[12] 李想,焦玉勇,邹俊鹏,等. 深部采煤覆岩移动和地表沉降研究[J]. 安全与环境工程,2022,29(2):32−38. LI Xiang, JIAO Yuyong, ZOU Junpeng, et al. Study on overlying strata movement and ground subsidence in deep coal mining[J]. Safety and Environmental Engineering, 2022, 29(2): 32−38.
[13] 王利,张修峰. 巨厚覆岩下开采地表沉陷特征及其与采矿灾害的相关性[J]. 煤炭学报,2009,34(8):1048−1051. WANG Li, ZHANG Xiufeng. Correlation of ground surface subsidence characteristics and mining disasters under super-thick overlying strata[J]. Journal of China Coal Society, 2009, 34(8): 1048−1051.
[14] 李春意,李彦辉,梁为民,等. 大采深巨厚砾岩综放开采地表沉陷规律[J]. 河南理工大学学报(自然科学版),2013,32(6):703−708. LI Chunyi, LI Yanhui, LIANG Weimin, et al. Research on surface subsidence law under condition of deep mining with thick overburden conglomerate based on field measurement datum[J]. Journal of Henan Polytechnic University(Natural Science), 2013, 32(6): 703−708.
[15] 李春意,崔希民,胡青峰,等. 常村矿巨厚砾岩下特厚煤层开采对地表形变的影响分析[J]. 采矿与安全工程学报,2015,32(4):628−633. LI Chunyi, CUI Ximin, HU Qingfeng, et al. An analysis of extra-thick coal mining influence on ground surface deformation under the condition of massive conglomerate stratum in Changcun colliery[J]. Journal of Mining & Safety Engineering, 2015, 32(4): 628−633.
[16] 关军琪,吕义清,赵国贞. 黄土沟谷区采空区充填对地表变形规律的影响研究[J]. 煤矿安全,2022,53(1):49−55. GUAN Junqi, LYU Yiqing, ZHAO Guozhen. Study on the influence of goaf filling on surface deformation in loess gully area[J]. Safety in Coal Mines, 2022, 53(1): 49−55.
[17] 曹琰波,范文,陶宜权,等. 榆神府矿区双煤层开采覆岩破坏及地面沉降特征研究[J]. 煤矿安全,2023,54(7):205−213. CAO Yanbo, FAN Wen, TAO Yiquan, et al. Research on overburden failure and land subsidence characteristics of double coal seam mining in Yushenfu Mining Area[J]. Safety in Coal Mines, 2023, 54(7): 205−213.
[18] 杨军伟,侯得峰. 厚松散层矿区采动程度对地表沉降特征的影响[J]. 煤矿安全,2017,48(4):52−54. YANG Junwei, HOU Defeng. Influence of mining degree on surface subsidence characteristics under the condition of mining thick unconsolidated layers[J]. Safety in Coal Mines, 2017, 48(4): 52−54.
[19] 姜福兴,叶根喜,王存文,等. 高精度微震监测技术在煤矿突水监测中的应用[J]. 岩石力学与工程学报,2008(9):1932−1938. JIANG Fuxing, YE Genxi, WANG Cunwen, et al. Application of high-precision microseismic monitoring technique to water inrush monitoring in coal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2008(9): 1932−1938.
[20] 孟祥军,赵鹏翔,王绪友,等. 大倾角高瓦斯煤层采动覆岩“三带”微震监测及瓦斯抽采效果[J]. 煤炭科学技术,2022,50(1):177−185. MENG Xiangjun, ZHAO Pengxiang, WANG Xuyou, et al. “Three zones”microseismic monitoring and analysis of gas drainage effect of overlying strata in gob of high dip high gas seam[J]. Coal Science and Technology, 2022, 50(1): 177−185.
[21] 崔峰,贾冲,来兴平,等. 缓倾斜冲击倾向性顶板特厚煤层重复采动下覆岩两带发育规律研究[J]. 采矿与安全工程学报,2020,37(3):514−524. CUI Feng, JIA Chong, LAI Xingping, et al. Research on development law of overlying rock two zones under repeated mining in extra-thickcoal seam with gently inclined and brusting liability roof[J]. Journal of Mining & Safety Engineering, 2020, 37(3): 514−524.
[22] 袁国涛,张明伟,王杰,等. 采动覆岩微震分区演化特征的数值模拟研究[J]. 煤炭科学技术,2023(8):36−46. YUAN Guotao, ZHANG Mingwei, WANG Jie, et al. Numerical simulation study on sub-regional evolution of microseismic characteristics of mining overburden rock[J]. Coal Science and Technology, 2023(8): 36−46.
[23] 蒋金泉,王普,武泉林,等. 上覆高位岩浆岩下离层空间的演化规律及其预测[J]. 岩土工程学报,2015,37(10):1769−1779. JIANG Jinquan, WANG Pu, WU Quanlin, et al. Evolution laws and prediction of separated stratum space under overlying high-position magmatic rocks[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1769−1779.
[24] 马富武,李杨,苏怀瑞,等. 硬厚岩层下覆岩裂隙演化特征及其致灾机理分析[J]. 煤炭工程,2023,55(2):93−97. MA Fuwu, LI Yang, SU Huairui, et al. Evolution characteristics of overlying rock fissures under hard and thick strata and the hazard mechanism analysis[J]. Coal Engineering, 2023, 55(2): 93−97.
[25] 乔伟,王志文,李文平,等. 煤矿顶板离层水害形成机制、致灾机理及防治技术[J]. 煤炭学报,2021,46(2):507−522. QIAO Wei, WANG Zhiwen, LI Wenping, et al. Formation mechanism, disaster-causing mechanism and prevention technology of roof bed separation water disaster in coal mines[J]. Journal of China Coal Society, 2021, 46(2): 507−522.
[26] 孙嘉琳,杨骁. 基于等效弹簧模型的裂纹Euler-Bernoulli梁弯曲变形分析[J]. 力学季刊,2015,36(4):703−712. SUN Jialin, YANG Xiao. Bending deformation analysis of the Euler-Bernoulli beam with effect of switching crack gap[J]. Chinese Quarterly of Mechanics, 2015, 36(4): 703−712.
[27] 欧阳煜,夏登科. Pasternak双参数地基上Euler-Bernoulli裂纹梁弯曲的解析解[J]. 力学季刊,,2021,42(4):685−695 OUYANG Yu, XIA Dengke. Analytical solution of bending deformation of the Euler-Bernoulli cracked beam on Pasternak two-parameter foundation[J]. Chinese Quarterly of Mechanics, 2021, 42(4): 685−695.
[28] 张明,姜福兴,李克庆. 巨厚岩层采场关键工作面防冲-减震设计[J]. 中南大学学报(自然科学版),,2018,49(2):439−447 ZHANG Ming, JIANG Fuxing, LI Keqing. Design of rock burst prevention and mine-quake reduction in key longwall panel under super-thick strata[J]. Journal of Central South University(Science and Technology), 2018, 49(2): 439−447.
计量
- 文章访问数: 22
- HTML全文浏览量: 5
- PDF下载量: 3
