Fine design modeling technology and intelligent implementation of through-layer drilling
-
摘要:
为了保障煤矿安全生产，进一步提高煤矿瓦斯防治能力，基于煤层瓦斯流动理论，从瓦斯有效抽采半径分析入手，建立数学模型，确定了穿层钻孔精细设计布孔控制关键指标；运用计算机建模技术对钻孔进行精细化验算，完成了煤矿井下底板穿层预抽瓦斯钻孔布置的精细化智能设计系统的开发，该系统能精准感知，并自主对给定区域钻孔复合验算，实现了钻孔设计过程中少人化、精细化，并与传统设计进行了对比分析。研究表明：采用精细化智能设计钻孔，最大限度地实现了煤体内钻孔轴线等密度分布，使钻孔工程比传统设计省工；可实现海量底板穿层钻孔的智能化设计，使钻孔施工抽采煤层瓦斯效果好，钻孔施工难度降低，显著提升了煤矿瓦斯防治能力和管理水平。
-
关键词:
- 瓦斯抽采 /
- 穿层钻孔 /
- 精细化智能布孔 /
- 抽采半径 /
- 钻孔布置智能设计系统
Abstract:In order to ensure the safety of coal mine production and further improve the ability of coal mine gas control, based on the theory of gas flow in coal seam, starting with the analysis of effective extraction radius of gas, a mathematical model is established to determine the key indexes of fine design layout control of through-layer holes. The computer modeling technology is used to carry out the fine checking calculation of the borehole, and the development of the fine intelligent design system for the borehole distribution design of the coal seam gas pre-pumping in the bottom layer of the coal mine is completed. The system can accurately perceive and independently check the borehole compound calculation in the given area, so as to realize the less human and fine drilling design process, and the analysis and comparison with the traditional design are carried out. The research shows that the use of fine intelligent drilling design can maximize the equal density distribution of the borehole axis in the coal body, and make the drilling project less than the traditional design. It can be seen that the intelligent design of massive floor through-layer drilling makes the drilling construction and coal seam gas extraction effect is good, the construction difficulty is reduced and the coal mine gas prevention and control ability and management level are significantly improved.
-
在煤矿井下，煤层瓦斯压力测定（比如胶囊-黏液封孔等）和钻孔瓦斯涌出初速度测定均需要向钻孔内送入封孔器。当封孔器在钻孔内移动时，封孔器端头与钻孔残留煤渣相互作用；一方面，钻孔残留煤渣会阻碍封孔器移动，另一方面，受封孔器端头力学作用，煤渣出现堆积现象；如果堆积严重，封孔器难以快速到达钻孔预定位置，参数测定可能失败（比如钻孔瓦斯涌出初速度测定，要求2 min内将封孔器送入预定位置并密封钻孔）。
为减轻钻孔残留煤渣对封孔器移动的影响，学者们从排渣和减阻2个方面进行了研究。在排渣方面：刘涛[1]提出了环缝式引射器输送钻孔煤渣技术；王永龙等[2-3]提出了双动力低螺旋钻杆排渣技术和刻槽钻杆排渣技术；杜长胜等[4]提出了脉动通风与钻杆分风联合作用排渣技术，李国强等[5]提出了旋风分离除渣技术；李栋等[6]提出了射流排水排渣技术；张辉等[7]提出了泵吸反循环钻进排渣技术；潘竞涛等[8]提出了下行定向钻孔氮气泡沫幂律多相流携渣解堵技术；汪义龙等[9]提出了煤层定向钻孔气举排渣技术；李成成[10]提出了“逐级升压切缝、低压旋转排渣”的排渣技术；张宏杰等[11]提出了“高螺旋机械排渣为主、液动排渣为辅”的复合排渣技术；童碧等[12]提出了基于整体式螺旋钻杆的复合排渣工艺技术；何将福等[13]提出了三通道反循环排渣技术；张宏钧等[14]提出了螺旋钻杆与压风复合排渣技术。在减阻方面：齐黎明等[15]提出了在封孔器前端安设锥面端头的减阻技术；周福宝等[16]提出了让高压气流从钻孔孔壁与抽采管之间流出，从而减轻煤渣阻碍抽采管移动的技术方案。
如果排渣技术过度使用，会扰动钻孔孔壁并产生新的煤渣甚至于塌孔；由此可见，排渣技术虽然可降低钻孔残留煤渣数量，但不能将残留煤渣清除；因此，仅采用排渣技术是不够的，需补充应用减阻技术。在封孔器前端安设锥面端头可以有效降低残留煤渣阻力[15]，是一种简单、实用的减阻技术；封孔器锥面端头（简称锥面端头）与钻孔残留煤渣的力学作用及其减阻机理是该技术推广应用中亟待解决的基础理论问题，并且锥面端头设计也需要进一步优化，在公开的文献资料中，未见相关研究成果。为此，从理论上分析锥面端头与钻孔残留煤渣的力学作用，探索锥面端头减阻机理，并进行工程应用。
1. 锥面端头前方钻孔残留煤渣堆积状况分类
锥面端头前方残留煤渣堆积状况如图1所示。
由图1可以看出，随着锥面端头移动，锥面端头前方堆积的残留煤渣（简称堆积煤渣）越来越厚。根据堆积煤渣是否超过锥面端头锥顶，锥面端头前方钻孔残留煤渣堆积状况可分为2类：堆积煤渣未超过锥顶和堆积煤渣超过锥顶。
2. 锥面端头移动最小推力理论分析
2.1 堆积煤渣未超过锥顶时的最小推力
假定锥面端头在钻孔内呈水平状态，以锥面端头锥底最低点O为原点，锥面端头移动方向（锥面端头轴线方向）为x轴正方向，垂直向上为z轴正方向，y轴正方向垂直于平面xOz，并指向右侧，建立直角坐标系，锥面端头受力分析如图2所示。
在图2中，锥面CAOB为锥面端头与煤渣的接触面（简称接触面），O1点为锥底圆心，2θ为锥面角度；C点为锥面上接触面与非接触面分界线的顶点，位于x轴正上方；h为堆积煤渣厚度。
锥面端头受力如下：封孔器推力F1整体作用于x轴正方向；重力G整体作用于z轴负方向；煤渣压力F2（挤压应力σ的总称）垂直于接触面并指向锥面端头内部；煤渣摩擦阻力F3与接触面相切并垂直于z轴（锥面端头以近水平形式移动，并不断破坏堆积煤渣的稳定性，与滑块在固定斜面的移动有着本质区别）。
为便于受力分析，需对煤渣压力与煤渣摩擦阻力沿x轴、y轴、z轴3个方向进行分解，并求出各分力计算方法。
y轴、z轴方向分力微元挤压应力分析如图3所示。由于图2中锥面CAO和锥面CBO沿平面CDO对称分布，因此，取锥面CBO进行分析即可。先作2个平行于yOz平面的截面（间距为dx），再从圆锥的中心轴线作2个截面（夹角为dβ），在锥面CBO上取微元（面积为ds），并进行受力分析。
![]()
图 3 y轴、z轴方向分力微元挤压应力分析Figure 3. Extrusion stress analysis of differential element for y-axis and z-axis component of force根据图3（a），微元面积可表示为：
$$ \mathrm{d}s=\frac{\mathrm{d}x}{\mathrm{c}\mathrm{o}\mathrm{s}\;\varphi }（H-x）\frac{r}{H}\mathrm{d}\beta $$ (1) 式中：s为锥面CBO的面积，m2；x为x轴坐标，m；φ为沿x轴方向的锥面角度，（°）；H为圆锥高度，m；r为锥面端头锥底半径，m；β为夹角，（°）。
根据图3（b），微元承受的挤压应力可分解为平行于x轴的分应力dF2x和沿着截面指向圆心的分应力dF2yz，dF2yz可表示为：
$$ {\mathrm{d}}{F}_{2{yz}}=\sigma （H-x）\frac{r}{H}{\mathrm{d}}x{\mathrm{d}}\beta $$ (2) 式中：F2yz为锥面CBO的煤渣压力沿着截面指向圆心分力，N；σ为接触面挤压应力，Pa。
对F2yz进行分解，力分解示意图如图4所示。
根据图4，F2yz平行于y轴的分力F2y可表示为：
$$ F_{2{{{y}}}}=\int_0^{\frac{h}{\mathrm{t}\mathrm{a}\mathrm{n}\; \theta}}\; \sigma（H-x）\frac{r}{H}（1-\mathrm{cos}\; \alpha）\mathrm{d}x $$ (3) 式中：F2y为F2yz平行于y轴的分力（锥面CBO的煤渣压力沿y轴方向分力），N；h为堆积煤渣厚度，m；θ为锥面端头锥面角度的1/2值，（°）；α为弧线对应夹角，（°）。
根据三角函数关系，有：
$$ （H-x）\frac{r}{H}（1-\mathrm{c}\mathrm{o}\mathrm{s}\;\alpha ）=h-x\mathrm{t}\mathrm{a}\mathrm{n}\;\theta $$ (4) 将式（4）代入式（3）并积分，有：
$$ {F}_{2{y}}=\sigma \frac{{h}^{2}}{2\mathrm{t}\mathrm{a}\mathrm{n}\;\theta }=\sigma {S}_{\vartriangle CDO} $$ (5) 式中：${S}_{\vartriangle CDO} $为$\vartriangle $CDO的面积，m2。
$\vartriangle $CDO为锥面CBO沿y轴的投影，因此，因此，锥面CBO的煤渣压力沿y轴方向分力等于挤压应力σ与投影面积SCDO之积。
同理，F2yz平行于z轴的分力F2z可表示为：
$$ {F}_{2{z}}={\int }_{0}^{\frac{h}{\mathrm{t}\mathrm{a}\mathrm{n}\;\theta }}\sigma （H-x）\frac{r}{H}\mathrm{s}\mathrm{i}\mathrm{n}\;\mathrm{\alpha }\mathrm{d}x $$ (6) 式中：F2z为F2yz平行于z轴的分力（锥面CBO的煤渣压力沿z轴方向分力），N。
根据三角函数关系，有：
$$ （H-x）\frac{r}{H}\mathrm{s}\mathrm{i}\mathrm{n}\;\mathrm{\alpha }=\sqrt{2Rh-{h}^{2}}（1-\frac{\mathrm{t}\mathrm{a}\mathrm{n}\;\theta }{h}x） $$ (7) 将式（7）代入式（6）并积分，有：
$$ {F}_{2{z}}=\sigma \frac{h}{2\mathrm{t}\mathrm{a}\mathrm{n}\;\theta }\;\sqrt{2Rh-{h}^{2}}=\sigma {S}_{\vartriangle CBD} $$ (8) 式中：${S}_{\vartriangle CBD} $为三角形CBD的面积，m2。
$\vartriangle $CBD为锥面CBO沿z轴的投影，因此，锥面CBO的煤渣压力沿z轴方向分力等于挤压应力σ与投影面积SCBD之积。
x轴方向分力微元挤压应力分析图如图5所示。图3中平行于x轴的微元分应力dF2x是φ的函数，由于φ非固定值，不便求解；为此，先作2个平行于xOy平面的截面（间距为dz），再作2个平行于xOz平面的截面（间距为dy），在锥面CBO上取微元（面积为ds），并进行受力分析。
![]()
图 5 x轴方向分力微元挤压应力分析图Figure 5. Extrusion stress analysis of differential element for x-axis component of force
同理，图5中微元面积可表示为：
$$ \mathrm{d}s=\frac{\mathrm{d}y}{\mathrm{s}\mathrm{i}\mathrm{n}\;\varphi }\mathrm{d}z $$ (9) 式中：y为y轴坐标，m；z为z轴坐标，m。
图5中微元承受的挤压应力平行于x轴的分应力dF2x可表示为：
$$ \mathrm{d}{F}_{2{x}}=\sigma \mathrm{d}y\mathrm{d}z $$ (10) 式中：F2x为锥面CBO的煤渣压力沿x轴方向分力，N。
对式（10）进行积分，有：
$$ {F}_{2{x}}=\frac{\sigma }{2}（{r}^{2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\frac{r-h}{r}-\sqrt{2rh-{h}^{2}}（r-h））=\sigma {S }_{BDO} $$ (11) 式中：SBDO为割圆BDO的面积，m2。
割圆BDO为锥面CBO沿x轴的投影，因此，锥面CBO的煤渣压力沿x轴方向分力等于挤压应力σ与投影面积SBDO之积。
同理，锥面CBO的煤渣摩擦阻力在x轴、y轴2个方向的分力F3x、F3y等于挤压应力σ、摩擦阻力系数f和投影面积（投影平面与分力方向平行且包含z轴，投影面积分别为SCDO、SBDO）之积，可表示为：
$$ {F}_{3{x}}=\sigma f{S}_{CDO}=\mathrm{\sigma }f\frac{{h}^{2}}{2\mathrm{tan}\;\theta } $$ (12) $$ {F}_{3{y}}=\frac{\sigma }{2}f（{r}^{2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\frac{r-h}{r}-\sqrt{2rh-{h}^{2}}（r-h）） $$ (13) 式中：F3x为锥面CBO的煤渣摩擦阻力沿x轴方向分力，N；F3y为锥面CBO的煤渣摩擦阻力沿y轴方向分力，N；f为锥面端头与煤渣的最大静摩擦系数。
当封孔器推力F1达到一定数值（最小推力F）时，锥面端头才能突破煤渣阻力向前移动，x轴、y轴、z轴3个方向的受力均处于平衡状态。y轴方向受力呈对称分布，自然平衡；x轴、z轴方向受力平衡方程可表示为：
$$ F=2{F}_{2{x}}+2{F}_{3{x}} $$ (14) $$ G=2{F}_{2\textit{z}} $$ (15) 式中：F为锥面端头移动最小推力，N；G为锥面端头重力，N。
将式（8）、式（11）、式（12）代入式（14）和式（15），并解方程，有：
$$\begin{split} &\begin{gathered} F = G\left(\mathrm{t}\mathrm{a}\mathrm{n}\; \theta\left(\frac{r^2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\; \frac{r-h}{r}}{h\sqrt{2rh-h^2}} - \frac{r-h}{h}\right) + f\sqrt{\frac{h}{2r-h}}\right) \\ 0 < h \leqslant r \end{gathered}\\[-16pt]& \end{split} $$ (16) 根据式（16）可知，锥面端头移动最小推力F与端头重力G、端头锥面角度的一半值θ、端头锥面与煤渣的最大静摩擦系数f属于正相关，与堆积煤渣厚度h和端头锥底半径r的相关性，无法直接判定。
假设端头重力G为50 N，端头锥面角度的一半值θ为30°，最大静摩擦系数f为0.1，通过数值计算并绘制得到的锥面端头移动最小推力F随堆积煤渣厚度h和端头锥底半径r的变化曲线如图6所示。
![]()
图 6 锥面端头移动最小推力与堆积煤渣厚度和端头锥底半径的关系曲线Figure 6. Relation curves between minimum thrust of cone end movement and height of accumulated coal dregs and cone base radius of end根据图6可知：锥面端头移动最小推力F与堆积煤渣厚度h和端头锥底半径r也属于正相关。
2.2 堆积煤渣超过锥顶时的受力分析
当堆积煤渣超过锥顶时，根据是否超过锥面端头锥底最高点，可将残留煤渣堆积情况进一步划分，本研究仅分析未超过锥面端头锥底最高点的情形。
锥面端头与煤渣发生力学作用的面积相当于整个锥面与非接触面的面积之差，并忽略锥面端头锥面上方煤渣重力。在式（16）中，令h=r，求得的F值乘以2，即为整个锥面与煤渣接触条件下的锥面端头移动最小推力；再令h=2r−h，求得的F值，即为非接触面与煤渣接触条件下的锥面端头移动最小推力；上述两者之差即为堆积煤渣超过锥顶时的锥面端头移动最小推力F，如式（17）：
$$\begin{split} &\begin{gathered} F=G\mathrm{t}\mathrm{a}\mathrm{n}\;\theta \left(\pi +\frac{f}{\mathrm{t}\mathrm{a}\mathrm{n}\;\theta}\left(1-\sqrt{\frac{2r}{h}-1}\right)-\right.\\ \left.\left. \frac{{r}^{2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\;\frac{h-r}{r}}{\left(2r-h\right)\sqrt{2rh-{h}^{2}}}+\frac{h-r}{2r-h}\right)\right. \qquad r < h \leqslant 2r \end{gathered}\\[-18pt]& \end{split} $$ (17) 3. 锥面端头移动最小推力试验研究
锥面端头移动最小推力F的影响因素较多，因篇幅受限，仅试验研究锥面端头移动最小推力随端头锥面角度的变化规律，并验证理论分析结果的可靠性。
试验方案如下：采用弹簧秤牵拉带有锥面端头的封孔器并让其在含煤渣的管道内匀速移动，弹簧秤显示读数即为锥面端头移动最小推力；锥面角度分别是60°、45°、30°、20°、18°、15°，共6组试验。试验装置设计图如图7所示，锥面端头移动最小推力与锥面角度的关系曲线如图8所示。
![]()
图 8 锥面端头移动最小推力与锥面角度的关系曲线Figure 8. Relation curves between minimum thrust of cone end movement and conical surface angle由图8可知：锥面角度增加，锥面端头移动最小推力升高，并且上升速率加快；移动距离越远，上升速率加快趋势越明显。根据式（16），锥面端头移动最小推力F与tan θ成正比，tan θ为正切函数，随θ增大而升高并且上升速度逐渐加快。由此可见，试验研究结果与理论分析结果基本一致。
4. 锥面端头减阻机理
与平面端头相比，锥面端头可以通过接触面对堆积煤渣施加平行于y轴的侧向力；因此，可通过分析侧向力来探索锥面端头减阻机理。因篇幅受限，以堆积煤渣未超过锥顶的情形为例，进行分析。
堆积煤渣承受的侧向力Fy是锥面端头y轴方向受力的反作用力，方向由接触面指向堆积煤渣，并平行于y轴，有：
$$ {F}_{{y}}={F}_{2{y}}-{F}_{3{y}} $$ (18) 将式（5）、式（13）、式（15）代入式（18），有式（19）：
$$\begin{split} &\begin{gathered} {F}_{{y}}=G\frac{h}{2\sqrt{2rh-{h}^{2}}}-\frac{G\mathrm{t}\mathrm{a}\mathrm{n}\;\theta }{h\sqrt{2rh-{h}^{2}}}f（{r}^{2}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\;\frac{r-h}{r}-\\ \sqrt{2rh-{h}^{2}}（r-h）） \end{gathered}\\[-19pt]& \end{split} $$ (19) 式中：Fy为堆积煤渣承受的侧向力，N。
根据式（19）可知，θ越小，Fy越大，即锥面端头越尖，Fy越大。
与锥面端头相接触的煤渣，在侧向力Fy的推动下，向钻孔孔壁侧移动（或被压缩）；导致锥面端头通过后，锥面端头后方残留煤渣增加，锥面端头前方堆积煤渣减少，堆积煤渣厚度h降低；锥面端头越尖，侧向力Fy越大，堆积煤渣厚度h越低。
锥面端头移动的突破点通常位于接触面顶端（堆积煤渣未超过锥顶时，在C点；堆积煤渣超过锥顶，在锥面端头锥顶），如果接触面顶端承受的应力超过该点的堆积煤渣剪切应力，则堆积煤渣遭到破坏、锥面端头可向前移动。
由于堆积煤渣相邻颗粒之间具有一定的咬合作用，图9（b）的某片煤渣薄板受侧向力挤压后，受压效应向前传递（距离越远，效应越弱），导致该煤渣薄板至钻孔孔壁一侧应力升高，而至钻孔中心一侧应力下降（相当于1根受压弹簧，从某个位置施加新力后，受压一侧弹簧绷紧程度加强，而另一侧弹簧绷紧程度减弱）；虽然煤渣属于散体，单片煤渣薄板微观上的受压效应传递能力较低，但是，当众多煤渣薄板的微观受压效应传递累积起来时，宏观上可以在一定程度上影响应力分布。
在全体煤渣薄板受压效应传递综合作用下，从C点到钻孔孔壁（E1、E2）的堆积煤渣应力变化如下：靠近C点一侧应力下降，靠近钻孔孔壁（E1、E2）一侧应力上升，C点（位于钻孔中心，并且距侧向力最近）应力下降大。根据散体动力学理论[17]，摩尔库伦破坏准则适用于散体，堆积煤渣剪切应力与正应力成正比。因此，受侧向力挤压效应传递的影响，堆积煤渣C点及其邻近区域的剪切应力降低，C点下降值最大。
综上所述，锥面端头减阻机理如下：锥面端头越尖（θ越小），侧向力Fy越大，堆积煤渣厚度h越低、接触面顶端及其临近区域堆积煤渣剪切应力越小，堆积煤渣对锥面端头移动的阻碍能力越弱。
注：C点及其邻近区域堆积煤渣受力破坏后，堆积煤渣整体失去稳定性，靠近钻孔孔壁（E1、E2）一侧堆积煤渣应力自然得到释放。
5. 封孔器端头优化改进与现场试验
根据锥面端头移动最小推力与影响因素的关系，可从以下几个方面对锥面端头开展优化设计：①采用低密度材料制作锥面端头，降低端头重力；②适当减小端头锥面角度；③采用喷漆等措施提高端头锥面的光滑性，降低端头锥面与煤渣的最大静摩擦系数；④采用更细的封孔器，从而减小端头锥底半径。
在文献[15]中，将1个空心外罩（锥面角度约20°）安设于钻孔瓦斯涌出初速度测定装置的封孔器端头，端头由台阶式转变为锥面式；在此基础上，根据锥面端头优化设计思路，对封孔器端头作进一步改进。
根据图8，当锥面角度较低时，降低锥面角度改变锥面端头移动最小推力的作用不大；由于端头锥底半径与封孔器主体部分一致，而主体部分需要考虑膨胀性能、耐压性能和膨胀液输送、内置管道气体流动阻力等因素，截面尺寸（目前为38 mm）很难进一步缩小。因此，从如下2个方面对封孔器端头进行改进：①将空心外罩的制作材料由不锈钢改合金，减轻端头质量；②对封孔器锥面端头打蜡，降低端头锥面与煤渣的最大静摩擦系数。
在开滦矿区钱家营矿1355工作面进行了钻孔瓦斯涌出初速度测定现场试验，现场试验数据见表1。
表 1 现场试验数据Table 1. Experimental data in field test封孔器型号 最高送入孔深/m 孔深/m 时间/min 原始型 16 8 1.2 10 1.3 12 1.5 14 1.7 16 2.0 改进型 >20 8 0.9 10 1.0 12 1.2 14 1.3 16 1.5 18 1.7 20 1.9 由表1可知：改进型封孔器送入阻力小、推进速度快、送入钻孔深度大。
6. 结 语
1）锥面端头与煤渣接触面所承受的煤渣压力沿x轴、y轴、z轴的分力均等于挤压应力与投影面积之积；锥面端头与煤渣接触面所承受的摩擦阻力沿x轴、y轴的分力也均等于挤压应力、摩擦阻力系数和投影面积之积。
2）从理论上推导了锥面端头移动最小推力计算公式，它与端头质量、端头锥面角度、端头锥面与煤渣的最大静摩擦系数、堆积煤渣厚度和端头锥底半径均具有正相关性，为锥面端头优化设计指明了方向。
3）锥面端头移动最小推力与锥面角度呈正切函数关系，随锥面角度增大而升高并且上升速度逐渐加快。
4）通过侧向力分析，揭示了锥面端头减阻机理；锥面端头越尖，侧向力越大，堆积煤渣厚度越低、接触面顶端及其临近区域堆积煤渣剪切应力越小，堆积煤渣对锥面端头移动的阻碍能力越弱。
5）根据锥面端头优化设计思路改进后的封孔器端头，可以降低送入阻力、提高送入速度与孔深。
-
![]()
图 1 2类布孔方式关系图
Figure 1. Relationship diagram between two types of drill hole arrangement methods
![]()
图 2 钻孔见煤层顶板点等间距精细分析图
Figure 2. Fine analysis diagram of evenly spaced coal seam roof points observed through drilling
![]()
图 3 穿煤段钻孔轴线等垂距精细分析图
Figure 3. Fine analysis diagram of equal-vertical distance of borehole axis in coal section
![]()
图 4 单孔抽采煤层瓦斯有效影响范围模型
Figure 4. Model of effective influence range of coal seam gas by single hole extraction
![]()
图 8 煤体内精细化智能设计钻孔密度分布图
Figure 8. Fine intelligent design of drilling density distribution graph in coal body
![]()
图 9 见煤顶板点等间距设计钻孔密度分析剖面图
Figure 9. Cross section graph of borehole density analysis with equal spacing design for coal roof points
表 1 设计钻孔工程量对比表
Table 1 Comparison of drilling quantities
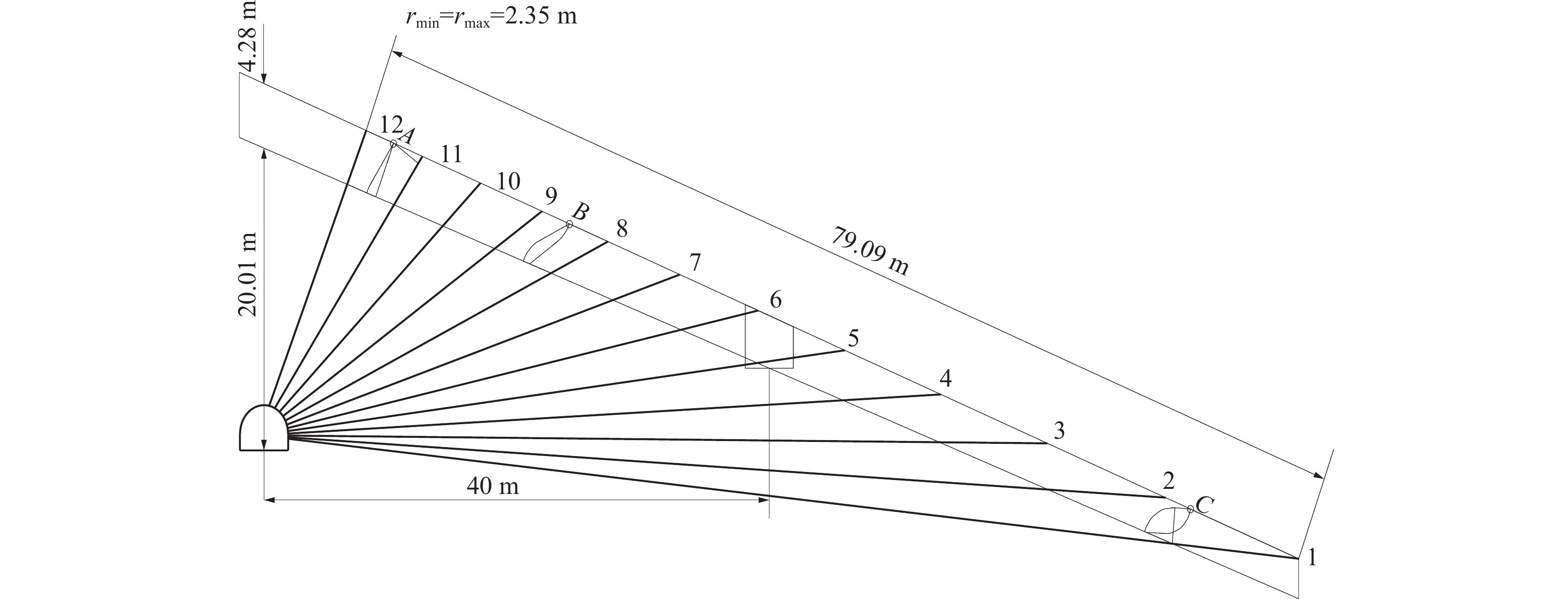
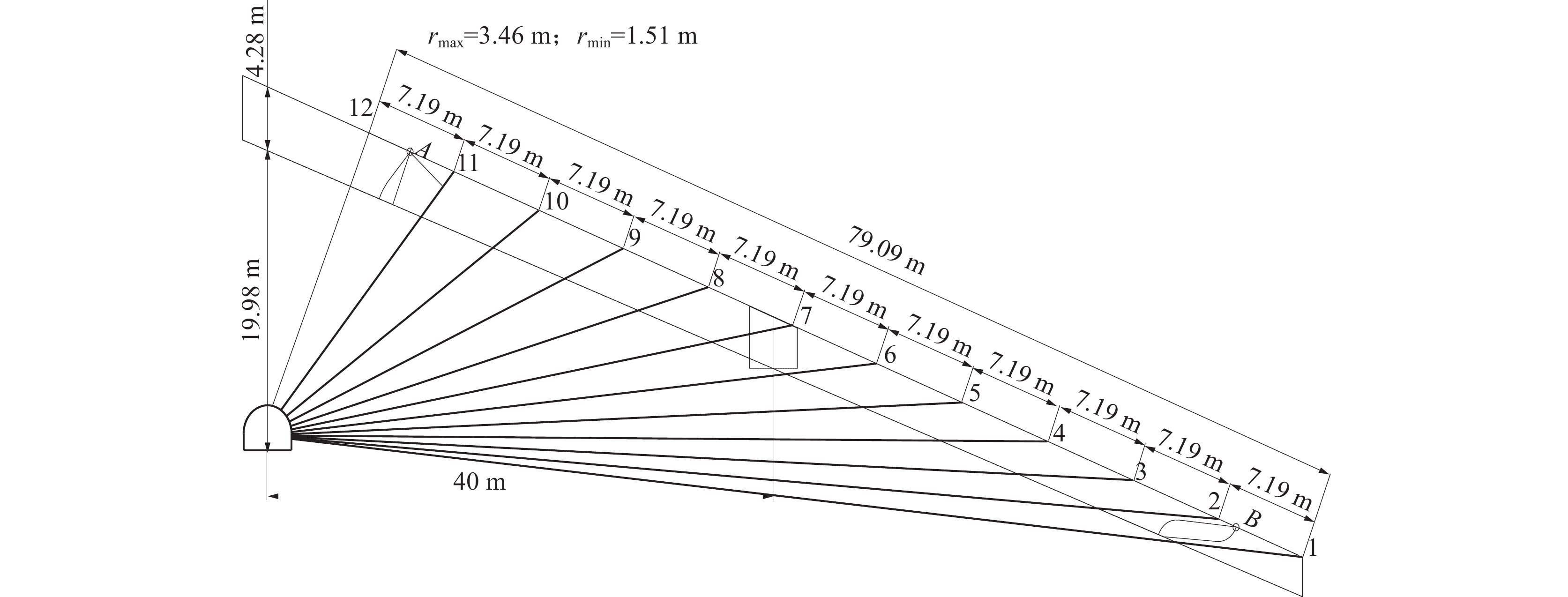
孔号 钻孔工程量/m 精细化设计 顶板等间距 1 80.402 80.402 2 69.600 73.515 3 60.125 66.583 4 51.745 59.757 5 44.414 53.123 6 38.065 46.485 7 32.663 40.257 8 28.155 34.299 9 24.583 28.847 10 21.968 24.214 11 20.353 20.995 12 19.767 19.767 合计 491.840 548.244 
下载: 导出CSV
-
[1] 中华人民共和国应急管理部,国家矿山安全监察管理局. 煤矿安全规程[M]. 北京:应急管理出版社,2022. [2] 张士岭. 普通钻孔智能设计系统研究与应用[J]. 煤炭工程,2019,51(6):149−152. ZHANG Shiling. Research and application of ordinary drilling intelligent design system[J]. Coal Engineering, 2019, 51(6): 149−152.
[3] 葛世荣,郝尚清,张世洪,等. 我国智能化采煤技术现状及待突破关键技术[J]. 煤炭科学技术,2020,48(7):28−46. GE Shirong, HAO Shangqing, ZHANG Shihong, et al. Status of intelligent coal mining technology and potential key technologies in China[J]. Coal Science and Technology, 2020, 48(7): 28−46.
[4] 王亮,孙毅民,褚鹏,等. 基于时空分布特征的煤层瓦斯测压准确性研究[J]. 中国安全科学学报,2021,31(2):40−47. WANG Liang, SUN Yimin, CHU Peng, et al. Study on accuracy of coal seam gas pressure measurement based on its spatial and temporal distribution characteristics[J]. China Safety Science Journal, 2021, 31(2): 40−47.
[5] 郝富昌,刘明举,孙丽娟. 瓦斯抽采半径确定方法的比较及存在问题研究[J]. 煤炭科学技术,2012,40(12):55−58. HAO Fuchang, LIU Mingju, SUN Lijuan. Study on comparison of methods to determine gas drainage radius and existed problems[J]. Coal Science and Technology, 2012, 40(12): 55−58.
[6] 徐遵玉. 穿层钻孔预抽煤层瓦斯有效半径考察方法研究[J]. 煤炭工程,2018,50(2):19−22. doi: 10.11799/ce201802005 XU Zunyu. Study on investigation method for effective drainage radius of drilling in coal seam gas pre-drainage[J]. Coal Engineering, 2018, 50(2): 19−22. doi: 10.11799/ce201802005
[7] 魏国营,秦宾宾. 煤体钻孔瓦斯有效抽采半径判定技术[J]. 辽宁工程技术大学学报(自然科学版),2013(6):754−758. WEI Guoying, QIN Binbin. Technology for determining effective drainage radius of coal seam drill hole[J]. Journal of Liaoning Technical University (Natural Science Edition), 2013(6): 754−758.
[8] 樊正兴. 基于抽采半径考察的回采工作面瓦斯预抽钻孔优化设计[J]. 煤炭工程,2019,51(6):103−107. FAN Zhengxing. Optimal design of gas pre-drainage boreholes in coal mining face based on investigation of drainage radius[J]. Coal Engineering, 2019, 51(6): 103−107.
[9] 袁亮. 淮南矿区煤矿煤层气抽采技术[J]. 中国煤层气,2006,3(1):7−9. YUAN Liang. Coal mine methane drainage technology in Huainan coal mining area[J]. China Coalbed Methane, 2006, 3(1): 7−9.
[10] 刘清泉,程远平,董骏,等. 煤层瓦斯流动理论简明教程[M]. 徐州:中国矿业大学出版社出版,2017. [11] 连昌宝,连杰. 多信息集成煤矿瓦斯防治钻孔工程自动化设计模型创建与展望[C]//2017年中国煤炭学会第五届瓦斯地质委员会第四次全国瓦斯地质学术年会论文集. 北京:中国煤炭学会,2017:103−111. [12] 张吉林,岳俊,谭瑶,等. 钻孔三维可视化系统构建与应用[J]. 煤炭技术,2017,36(10):106−108. ZHANG Jilin, YUE Jun, TAN Yao, et al. Constructionand application of 3D borehole visualization system[J]. Coal Technology, 2017, 36(10): 106−108.
[13] 李钢,范喜生,马丕梁,等. 基于MATLAB的本煤层瓦斯抽采钻孔间距设计[J]. 煤矿安全,2011,42(1):35−37. LI Gang, FAN Xisheng, MA Piliang, et al. The design for space of gas drainage drills of the coal seam based on MATLAB[J]. Safety in Coal Mines, 2011, 42(1): 35−37.
[14] 周世宁,林柏泉. 煤层瓦斯赋存与流动理论[M]. 北京:煤炭工业出版社,1999. [15] 国家煤矿安全监察局. 防治煤与瓦斯突出细则[M]. 北京:煤炭工业出版社,2019. [16] 国家安全生产监察管理总局,国家发展和改革委员会,国家能源局,等. 煤矿瓦斯抽采暂行规定[M]. 北京:煤炭工业出版社,2011. [17] 马国龙. 瓦斯抽出定向长钻孔智能设计方法及系统[J]. 煤矿安全,2017,48(5):103−106. MA Guolong. Intelligent design method and system for long directional gas drainage drilling[J]. Safety in Coal Mines, 2017, 48(5): 103−106.
[18] 徐乃忠,涂敏. 三维立体瓦斯抽采钻孔程序设计及应用[J]. 煤矿安全,2013,44(9):17−19. XU Naizhong, TU Min. Program design and application of three-dimensional gas extraction drilling[J]. Safety in Coal Mines, 2013, 44(9): 17−19.
计量
- 文章访问数: 30
- HTML全文浏览量: 3
- PDF下载量: 3
