Roof water inrush risk assessment based on LDA-RBF and comprehensive weighting method
-
摘要:
为了解决龙凤煤矿9号煤层开采过程中顶板突水危险性问题,采用线性判别分析法(LDA)构建1种LDA-RBF神经网络导水裂隙带发育高度预测模型,并基于改进CRITIC评价法结合层次分析法(AHP)建立了CRITIC-AHP综合赋权法,分别评价矿区顶板采裂危险性及含水层富水性等级;通过ArcGis地理信息处理技术,将采裂危险性分区与富水性分区叠加,得到9号煤层顶板突水危险性综合分区图。结果表明:LDA-RBF神经网络预测模型结构简单且拟合精度更高,9号煤层导水裂隙带发育预测高度为50.4 m,已超过区域内大部分含水层底界标高,表明大部分区域存在较高的采裂危险性;而改进后的综合赋权法避免了评价结果主客观性过强的问题,其富水性分区结果与钻孔实际涌水量相符;突水危险区主要在矿区中北部呈条状分布,这是该区域含水层富水性较强和采裂危险性较高共同作用的结果,因此,在实际开采中应对以上区域予以重视。
Abstract:In order to solve the problem of roof water inrush risk during the mining of No. 9 coal seam in Longfeng Coal Mine, an LDA-RBF neural network model for predicting the development height of water-conduction fracture zone was constructed by linear discriminant analysis (LDA), and a CRITIC-AHP comprehensive weighting method was established based on the improved CRITIC evaluation method combined with analytic hierarchy method (AHP) to evaluate the risk of roof cracking and the water richness level of the aquifer in the mining area. Through ArcGis geographic information processing technology, the cracking risk zone and the water-rich zone are superimposed to obtain a comprehensive zoning map of the water inrush risk of the roof of No.9 coal seam. The results show that the LDA-RBF neural network prediction model has a simple structure and higher fitting accuracy, and the development prediction height of the No.9 coal seam water-conducting fracture zone is 50.4 m, which has exceeded the bottom boundary level of most aquifers in the area, indicating that there is a high risk of cracking in most areas. The improved comprehensive weighting method avoids the problem of excessive subjectivity and objectivity of the evaluation results, and the water-rich zoning results are consistent with the actual water inflow of the borehole. Finally, the water inrush danger zone is mainly distributed in strips in the central and northern parts of the mining area, which is the result of the combined effect of strong water richness and high cracking risk of the aquifer in this area, indicating that the above areas should be paid attention to in actual mining.
-
煤矿水害是矿井安全生产中5大灾害之一,随着我国煤矿开采向深部发展,水害问题愈加严重[1],制约了煤矿的安全高效开采,因此,准确评价矿区突水危险性是水害防治与预警的关键工作之一。针对煤矿突水危险性评价问题,相关学者从不同角度做了大量工作。李博等[2]基于西南地区岩溶地下水赋存特征,构建了较为全面的西南地区煤层顶板岩溶含水层富水性评价指标体系;龙良良等[3]提出了层次分析法结合熵权法综合评价顶板突水危险性的方法;侯恩科等[4]采用随机森林算法对风化基岩含水层富水性进行预测,并结合围岩松动圈划分了巷道掘进顶板安全性分区;周全超等[5]通过拉格朗日乘子法改进层次分析法与熵权法,并引入富水性指数法构建了煤层顶板富水性评价模型;LIU等[6]基于专家评分法及突变理论预测了西北侏罗系煤田顶板突水综合评价风险,其成果为侏罗系煤田开采工作面参数的设计与优化提供了一定依据;XIE等[7]通过偏差平方和优化现有评价方法得到的主客观权值,有效提高了模型判别准确性。此外,顶板突水方法还有可拓聚类分析方法[8]、模糊可变集[9]、灰色关联法[10]、因子分析法[11]等。
上述学者对顶板突水危险性评价与预测研究做了大量贡献,并提出一系列评价方法,煤矿突水评价理论也日趋完善,但还存在一定的改进空间。首先,准确判别导水裂隙带的发育高度是顶板突水危险性评价结果合理的前提,经验公式法和相似模拟是目前应用较为广泛的2种导水裂隙带发育高度确定方法,但经验公式法与实测结果往往存在一定差异,相似模拟法存在工作量较大等问题,因此,寻求1种高效且准确的导水裂隙带发育高度确定方法尤为重要;其次,现有突水评价方法多从主观角度出发或过于依赖因素间数据的相互关系,导致评价结果存在一定的缺陷。
为此,针对上述问题及前人研究基础,以“三图法”[12]为基本理论,采用线性判别分析法对大量导水裂隙带实测高度样本降维并分类处理,通过RBF神经网络对处理后样本学习训练,构建LDA-RBF导水裂隙带发育高度预测模型,以量化顶板冒裂安全性;针对现有单一评价方法存在的主客观性过强问题,在引入CRITIC评价法的基础上对其进行改进,并结合层次分析法建立CRITIC-AHP综合赋权评价法,以评价顶板含水层富水等级;使用ArcGis绘制相关图层并叠加,得到顶板突水危险性分区预测结果,为矿区防治水措施制定提供指导意义。
1. 工程概况
龙凤煤矿地处黔北高原,区内岩溶发育但具有不均一性,矿区地层从老到新分别为:茅口组、龙潭组、长兴组,夜郎组沙堡湾段、玉龙山段、九级滩段。水文地质概化模型如图1所示。
夜郎组玉龙山段、长兴组、茅口组为可溶岩类,溶蚀裂隙发育,富水性强。区内地表断层不发育,除1条贯穿采区生产巷道断层导水性较好外,其余断层均不导水,且对煤矿开采影响较小。全区主采9#走向较为平缓,煤层倾角平均为7°;顶板岩性以砂岩、泥岩、泥质粉砂岩为主,顶板距上覆长兴组含水层底界一般不足60 m,开采裂隙极易导通上覆长兴组含水层,威胁工作面作业安全。2019年8月21日,龙凤煤矿9#煤层5914采面发生顶板事故,由于作业区域导通上覆长兴组含水层,导致顶板受浸泡失稳垮塌。因此,对9#煤层顶板突水危险性进行综合评价,有利于矿区制定针对性防治水措施。
2. 冒裂安全性评价
2.1 LDA-RBF神经网络模型的建立
RBF算法是1种前馈型神经网络模型[13],由输入层、隐含层、输出层组成,具有拟合精度高的特点,几乎能以任意精度逼近非线性函数,但当数据量较多时,可能导致其网络结构变得复杂且难以收敛,因此,需要对输入层数据做降维处理,以提高RBF收敛速度及预测精度。
由于导水裂隙带数据间存在不同顶板岩性结构类型差异,选用线性判别分析对样本数据降维,不同于主成分分析法,LDA在对原始数据降维处理时,可以在保持数据分类的前提下将初始数据维度减少,降低数据的复杂程度。为此,提出并构建了1种基于LDA-RBF的神经网络导水裂隙带高度预测模型,改进了多维数据输入时RBF神经网络结构较为复杂等问题。
根据前人研究成果[14-16]并结合矿区工程实际,选取开采厚度、开采深度、工作面斜长、煤层倾角、顶板覆岩结构,作为神经网络输入层参数的32组导水裂隙带高度实测样本集[17-18],根据直接顶岩性与基本顶岩性的不同组合将顶板类型赋值为Ⅰ(硬-硬)、Ⅱ(硬-软)、Ⅲ(软-硬)、Ⅳ(软-软)。国内部分矿区导水裂隙带实测数据见表1。
表 1 国内部分矿区导水裂隙带实测数据Table 1. The measured data of water conducting fracture zone in some mining areas in China编号 开采
深度/
m开采
厚度/
m工作面
斜长/
m煤层
倾角/
(°)顶板
类型Ⅲ导水裂隙
带高度/
m1# 89 2.00 114 7.0 Ⅰ 45.00 2# 117 3.40 205 2.0 Ⅲ 72.00 3# 89 2.03 69 7.0 Ⅱ 45.86 4# 282 4.00 71 8.0 Ⅲ 33.00 5# 328 2.00 78 7.0 Ⅱ 23.00 ︙ ︙ ︙ ︙ ︙ ︙ ︙ 30# 86 4.60 170 7.0 Ⅱ 53.00 31# 396 3.45 160 14.0 Ⅲ 26.70 32# 168 3.00 137 5.5 Ⅳ 27.50 建立初始样本集后,使用LDA降维法对表1样本降维,主要有以下流程:
1)求解类内散度矩阵SW。SW反映了相同顶板类型数据属性点的聚集程度,SW可按下式确定:
$$ {{\boldsymbol{S}}_{\mathrm{w}}} = \displaystyle\sum\limits_{j = 1}^k {\displaystyle\sum\limits_{x \in {X_j}} {(x - {\mu _j})(} } x - {\mu _j}{)^{\mathrm{T}}} $$ (1) 式中:k为样本种类;Xj为j类样本的集合(j=1,2,···,k);x为对应种类下的样本值;μj为j类样本均值向量。
2)求解类间散度矩阵Sb。Sb反映了不同顶板结构数据间的离散程度,Sb可按下式确定:
$$ {{\boldsymbol{S}}_{\mathrm{b}}} = \displaystyle\sum\limits_{j = 1}^k {{N_j}} ({\mu _j} -{\boldsymbol{ \mu}} ){({\mu _j} - {\boldsymbol{\mu }})^{\mathrm{T}}} $$ (2) 式中:Nj为j类样本个数(j=1,2,···,k);μ为所有样本均值向量。
3)计算矩阵S−1WSb,得到m个特征值及对应的m维特征向量,以顶板类型作为LDA需考虑的分类因素,将导水裂隙带发育高度作为神经网络预测模型输出值,故只需对开采深度、开采厚度、工作面斜长、煤层倾角共4维数据降维处理,得到4个特征值及其对应的特征向量。
4)提取最大的d个特征值及对应的特征向量组成的矩阵W。
5)组成降维后特征数据集Li=WTXi,降维后的样本数据集Z={Li,K},其中:Xi为初始数据,WT为矩阵W的转置矩阵。
上述流程由MATLAB编程实现,得到降维后各因素最大主特征值分别为0.400、0.290、7.31×10−17、0.040,前2个因素累计贡献率达到94.52%,因此,选取主特征值0.4、0.29作为最大主特征值,其对应的特征向量矩阵W分别为[−0.015 2, 1.000 0, −0.004 7, 0.045 0]、[0.024 2, 1.000 0, −0.027 3, 0.087 0],矩阵W表示初始数据以特征向量为方向投影。
将初始数据沿着特征向量W投影后,得到降维后的特征数据集Li,此时影响导水裂隙带发育高度的5维因素降至3维,减少了RBF神经网络输入层个数,有利于提高收敛速度。
本次采用MATLAB构建LDA-RBF神经网络模型对上述样本进行学习训练,将降维后的样本参数及顶板类型作为LDA-RBF神经网络的输入层,将导水裂隙带高度作为神经网络输出层。取前28维数据作为神经网络训练集样本,29至32维数据作为测试集样本。需要注意的是,RBF神经网络拟合精度受spread系数影响(spread>0),当spread系数减小时,训练集样本拟合较好,但过小存在对训练集过拟合问题,即对训练集拟合精度高,对测试集拟合精度低;当spread系数增大时,对测试集拟合精度较高。同理,较大的spread系数存在对测试集过拟合的问题,因此spread系数的选择需要同时兼顾训练集和测试集的精度,此外,不同神经网络结构的最佳spread参数不同,为筛选出最优spread参数,经过测试将spread系数从1增加到500并分别训练与检验。
2.2 预测结果及冒裂安全性分区
训练结果表明:当spread系数为188时,LDA-RBF神经网络模型拟合效果最好;当spread系数为137时,RBF神经网络模型拟合效果最好,其结果对比见表2。
表 2 LDA-RBF与RBF模型导水裂隙带高度实测值与预测值对比Table 2. Comparison between the measured and predicted values of the height of water-conducting fracture zone in LDA-RBF and RBF models样本
编号顶板
类型实测高度/
m预测高度/m 预测高度相对误差/% LDA-RBF RBF LDA-RBF RBF 29# 1 72.0 72.05 0.07 72.76 1.06 30# 2 53.0 50.18 5.32 42.08 20.60 31# 3 26.7 25.55 4.31 22.90 14.23 32# 4 27.5 25.67 6.65 30.12 9.52 预测结果表明:LDA-RBF神经网络模型预测模型优于RBF神经网络预测模型,LDA-RBF拟合结果平均相对误差为4.09%,而RBF平均相对误差为11.35%,且30号样本误差达20.6%,整体预测精度较低。
LDA-RBF神经网络预测值更加接近实测值,其在减少数据维度的同时大幅提高了网络预测精度。因此,基于LDA-RBF的神经网络导水裂隙带高度预测模型,根据龙凤煤矿生产资料,9#煤层某工作面斜长178 m,顶板结构类型为Ⅲ(软-硬),覆岩岩性为中硬,开采深度180 m,采高3 m,煤层倾角7°,通过LDA算法将降维后样本参数代入LDA-RBF神经网络模型预测得到导水裂隙带高度为48.42 m。导水裂隙带发育高度Hli经验公式为[19]:
$$ {H_{{\mathrm{li}}}} = \frac{{100\displaystyle\sum\limits M }}{{1.6\displaystyle\sum \limits M{ + 3.6} }} \pm 5.6 $$ (3) 式中:M为煤层的采高。
由式(3)可得龙凤煤矿9#煤层导水裂隙带理论计算高度为41.3 m,取LDA-RBF拟合平均相对误差4.09%,得到龙凤煤矿9#煤层工作面回采导水裂隙带预测高度为46.46~50.40 m,由此可见,经验公式与预测值存在一定误差,鉴于神经网络的拟合效果较好,取50.40 m作为龙凤煤矿9煤层的导水裂隙带发育高度。
根据地质资料,9#煤层上距离长兴组含水层底界为30~52 m,平均39 m,对比预测结果,掘进过程中大部分区域内导水裂隙将发育至长兴组含水层,因此,把导水裂隙带高度与煤层顶板到长兴组含水层底板距离进行对比,将未超过含水层底板标高区域划分为安全区,导水裂隙带对含水层扰动破坏越大,冒裂危险性越高[20];而长兴组厚度为39 m,因此分别按导水裂隙带贯穿长兴组含水层厚度比例阈值(0%、15.38%、30.76%、46.15%)绘图,使用ArcGis绘制的龙凤煤矿冒裂安全性分区图如图2所示。
3. 含水层富水性评价与分区
3.1 含水层富水性评价指标
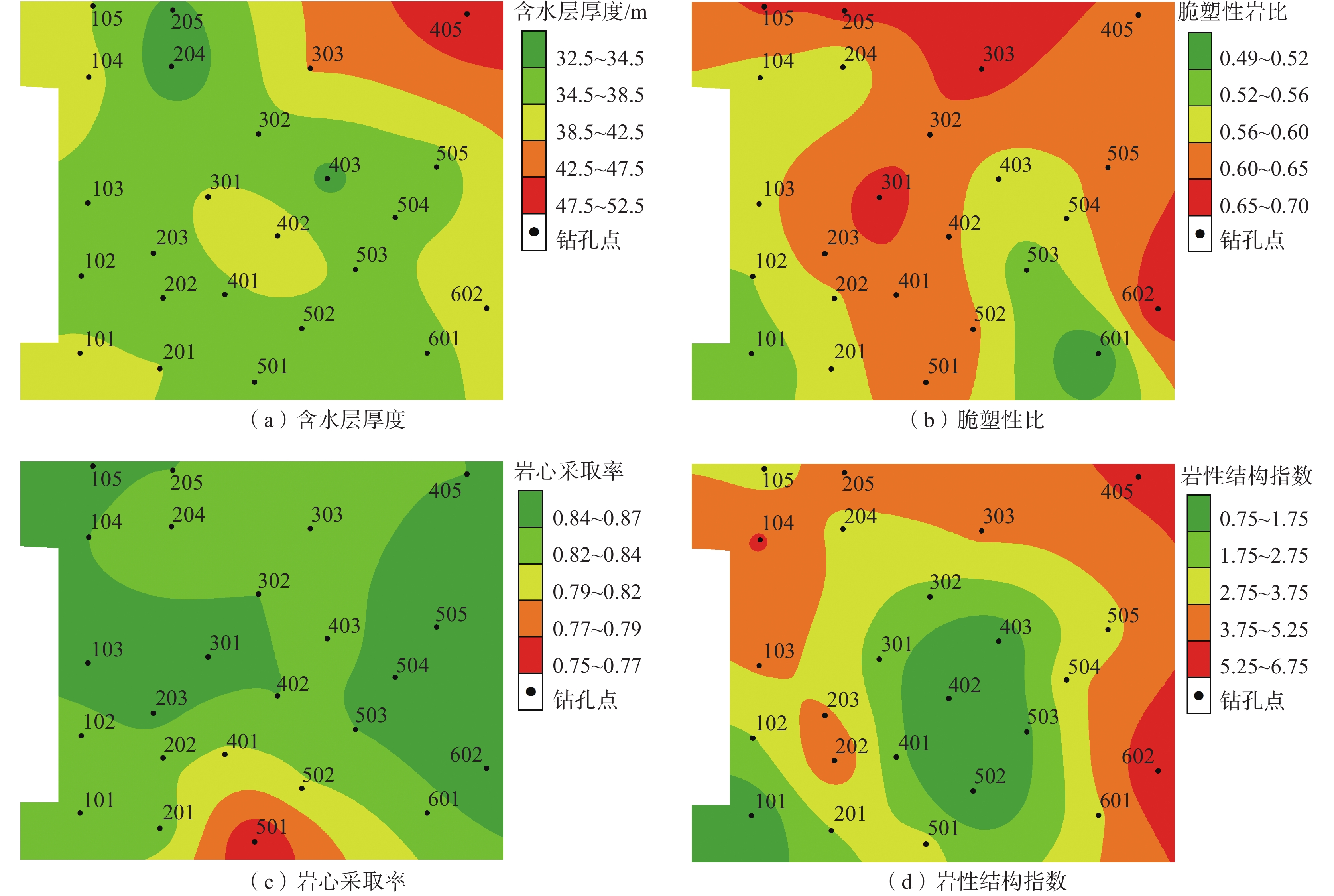
综合考虑各因素对含水层富水性影响,参考以往富水性评价经验,结合矿区现有地质资料,选取含水层厚度、脆塑性岩厚度比、岩心采取率、岩性结构系数作为含水层富水性主控因素。其中:含水层厚度反映储水空间大小,一定条件下,含水层厚度越大,富水性越强;脆塑性岩厚度比反映了地层结构中,受应力作用更易破碎,并增加导水性的脆性岩占比,比值越大,岩体越容易破碎,导水性越好;岩心采取率能代表岩层裂隙发育程度,岩心采取率越低则裂隙越发育。此外,一般而言,岩层中粒径较大的砂岩比粒径小的砂岩储水和导水性强,因此,以岩性结构指数表征砂岩发育特征,如式(4):
$$ K=\left(0.2a+0.7b+0.85c+d\right)e $$ (4) 式中:K为岩性结构指数;a、b、c、d分别为粉砂岩、细砂岩、中砂岩、粗砂岩厚度;e为结构系数。
结构系数值取决于岩层中砂岩厚度占比:①当占比大于70%时,取值为1;②当占比为70%~50%时,取值为0.8;③当占比为55%~45%时,取值为0.6;④当占比为45%~20%时,取值为0.4;⑤当占比小于20%时,取值为0.2。
按自然间断法做出的上述因素对应的各主控因素专题图层如图3[21-23]所示。
3.2 选取因素权重确定
为确定上述因素对含水层富水性的贡献程度,引入CRITIC评价法对主控因素赋权。CRITIC法是1种客观赋权法,主要考虑了数据间的波动性和冲突性,其中波动性可以认为是对比强度,用标准差表示,即某因素在不同钻孔中的数值差异,差异越大则权重越大;冲突性可以认为是不同因素间的相关性,不同因素的数据间相关系数越小,冲突性越小,权重也越小。
CRITIC评价法主要有以下流程:
1)对初始数据无量纲化。正向指标、逆向指标计算公式分别如式(5)和式(6):
$$ {X'_{ij}}=\frac{{X}_{ij}-{X}_{\min}}{{X}_{\max}-{X}_{\min}} $$ (5) $$ {X'_{ij}}=\frac{{X}_{ij}-{X}_{\min}}{{X}_{\max}-{X}_{\min}} $$ (6) 式中:$ {X'_{ij}} $为无量纲化值;Xij为对应的参数值;Xmax为参数中最大值;Xmin为参数中最小值,且此处对岩心采取率做逆向无量纲化,其余因素正向无量纲化。
2)计算数据间标准差。
$$ \overline {X}_{j}=\frac{1}{n}\displaystyle\sum\limits_{i=1}^{n}{X}_{ij} $$ (7) $$ {S}_{j}=\sqrt{\frac{\displaystyle\sum\limits_{i=1}^{n}{({X}_{ij}- \overline{X}_{j})}^{2}}{n-1}} $$ (8) 式中:$\overline {X}_{j} $为参数平均值;n为参数个数;Sj为第j个参数的标准差。
3)计算数据间相关系数。
$$ {f_j} = \displaystyle\sum\limits_{i = 1}^m {(1 - {r_{ij}})} $$ (9) 式中:fj为数据间冲突性;rij为不同指标间相关系数;m为主控因素个数,此处为4个。
4)计算信息量$ {C}_{j} $。
$$ {C}_{j}={S}_{j}\times {f}_{j} $$ (10) 5)确定因素权重$ {W}_{j} $。
$$\begin{split} &\;\\[-9pt] \begin{gathered}{W}_{j}=\frac{{C}_{j}}{\displaystyle\sum \limits_{j=1}^{m}{C}_{j}} \end{gathered}\\[-16pt]& \end{split}$$ (11) 使用MATLAB对上述流程编程,计算得到各因素权重值分别为:含水层厚度0.29,岩性结构指数0.30,脆塑性比0.18,岩心采取率0.23。
含水层厚度权重值为0.29,低于岩性结构指数权重,显然,这与前人研究结果及工程实际存在较大差异[24]。经过分析发现,在CRITIC算法流程中权重大小完全依赖于数据间的客观关系,而某些因素间其实并无直接关系,即CRITIC法默认不同因素间都存在相关性。因素间相关系数矩阵见表3。
表 3 因素间相关系数矩阵Table 3. Matrix of correlation coefficient between factors因素 含水层
厚度岩性结构
指数脆塑
性比岩心
采取率含水层厚度 1.000 0 −0.3515 0.5438 0.1004 岩性结构指数 −0.3515 1.000 0 0.3162 −0.2519 脆塑性比 0.5438 0.3162 1.000 0 −0.0914 岩心采取率 0.1004 −0.2519 −0.0941 1.000 0 根据因素之间的关系对相关系数矩阵进行如下修正:实际情况下含水层厚度与岩性结构指数并无直接关系,因此对其相关系数乘以修正系数0;同理,由于该矿含水层主要是石灰岩构成,因此,可以认为基于数据值计算得到的相关系数0.5438是合理的;对其乘以修正系数1,岩心采取率仅反映了岩石破碎程度,与含水层厚度并无直接关系;对其乘以修正系数0,以此类推,可以认为岩性结构指数及脆塑性比均与岩心采取率没有直接关系,而岩性结构指数与脆塑性比存在相关性,在MATLAB中按以上逻辑对原相关系数矩阵点乘以1个相关系数进行修正,相关系数修正矩阵见表4,修正后相关系数矩阵见表5。
表 4 相关系数修正矩阵Table 4. Correlation coefficient correction matrix因素 含水层
厚度岩性结构
指数脆塑性比 岩心
采取率含水层厚度 1 0 1 0 岩性结构指数 0 1 1 0 脆塑性比 1 1 1 0 岩心采取率 0 0 0 1 表 5 修正后相关系数矩阵Table 5. Corrected correlation coefficient matrix因素 含水层
厚度岩性结构
指数脆塑性比 岩心
采取率含水层厚度 1.000 0 0 0.543 8 0 岩性结构指数 0 1.000 0 0.316 2 0 脆塑性比 0.5438 0.312 6 1.000 0 0 岩心采取率 0 0 0 1 经过修正后,上述因素权重值分别为0.29、0.27、0.20、0.24,虽然结果较之前更加合理,但也揭示了客观评价法有时过于依赖数据的缺点。针对主客观评价法自有的局限性,在CRITIC法评价结果基础上,引入层次分析法构建1种CRITIC-AHP综合赋权法;AHP是1种主观评价方法,在征求专家意见的基础上,将不同因素按特征分类分层,并分别比较和打分量化,最后,将分值汇总构建因素矩阵,根据排序算法确定因素权重,并通过一致性检验标准判断权重是否符合逻辑。CRITIC-AHP法综合权重可按下式确定:
$$ {S _j} = \frac{{\sqrt {{\beta _j}{W_{gj}}} }}{{\displaystyle\sum\nolimits_{j = 1}^n {\sqrt {{\beta _j}{W_{gj}}} } }} $$ (12) 式中:Wgj为改进CRITIC法各权重值;βj为基于层次分析法的权重值。
综合赋权法的各主控因素权重值见表6。
表 6 各主控因素权重值Table 6. Weight value of each main control factor权重 含水层
厚度岩性结构
指数脆塑
性比岩心
采取率CRITIC权重 0.29 0.27 0.20 0.24 AHP权重 0.37 0.21 0.23 0.19 CRITIC-AHP组合权重 0.33 0.24 0.22 0.21 由表6可知:基于CRITIC-AHP的综合赋权法有效避免了单一评价法过于客观或主观的问题,其评价结果较为合理;含水层厚度权重值最大,是影响含水层富水性的最主要因素,而岩心采取率对富水性强弱贡献最小。
3.3 富水性分区与验证
根据上述各主控因素权重值,在建立的富水性评价模型基础上,引入富水性指数法,以评价矿区各钻孔处富水性指数值。富水性指数值代表了含水层富水程度,其值在0~1之间;数值越大,说明该处富水性越好。富水性指数Ⅵ可按式(13)进行确定[25-26]:
$$ \mathrm{V}\mathrm{I}=\displaystyle\sum \limits_{k=1}^{m}{W}_{k}{f}_{k}\left(x,y\right) $$ (13) 式中:Wk为各主控因素权重值;fk为各主控因素的值;x、y为地理坐标,表示钻孔的地理位置。
将上述各主控因素权重值代入式(13)得:
$$ \begin{split} &\begin{gathered} {\mathrm{VI}} = 0.33{f_1}(x,y) + 0.24{f_2}(x,y) + 0.22{f_3}(x,y) + \\ 0.21{f_4}(x,y) \end{gathered}\\[-16pt]& \end{split} $$ (14) 将无量纲化后的各主控因素值代入式(14),通过ArcGis自带的数据频率统计功能和自然间断法[27],将富水性由强至弱分为5个区:强富水性区(0.66~0.84)、较强富水性区(0.56~0.66)、中等富水性区(0.46~0.56)、较弱富水性区(0.36~0.46)、弱富水性区(0.26~0.36)。
利用ArcGis强大的空间分析功能得到的含水层富水性分区图如图4所示。
由图4可知:强富水性区主要分布在矿区东北方向,并在中西部呈长条状过渡。造成该现象的主要原因是:就含水层厚度等因素而言,矿区东北部数值明显高于其他区域,虽然岩层在矿区南部发育更为破碎,但在整个矿区范围内相差程度并不大(区内岩心采取率为0.752~0.872)。
为验证综合赋权法评价结果的合理性,以钻孔201、205、402长兴组含水层抽水试验结果验证含水层富水性,试验孔径均为110 mm,并对长兴组含水层以外地层下套管,避免和长兴组产生水力联系。
钻孔205在较长时间抽水后,水位下降速度仍然较慢,且在停止抽水后,迅速恢复至接近初始静止水位水平,证明该处水力补给较好;同时,钻孔205含水层富水性也明显高于其余2个钻孔,说明基于CRITIC-AHP综合赋权法的含水层富水性分区评价结果与实际水文勘探结果吻合,验证了该方法的准确性。
4. 顶板突水危险性评价
顶板突水可以认为是裂隙动态发育沟通上覆含水层的过程,即当采动裂隙顶端发育超过含水层底板标高时,导水通道形成,突水事故发生。首先,在结合矿区地质特点的基础上,充分征求专家意见,按上述研究结果提出了矿区突水危险性分区[20],不同的评价区划分标准不尽相同;其次,使用ArcGis对冒裂安全性分区图和富水性分区图进行叠加,并根据顶板突水划分标准对不同的区域进行筛选并赋予标示值;最后,将相同标示值的区域合并为1个区,最终得到9#煤层顶板突水危险性分区。顶板突水划分标准见表7,顶板突水危险性分区如图5所示。
表 7 顶板突水划分标准Table 7. Roof water bursting risk evaluation standard
富水性指数顶板突水分区 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ 0.26~0.36 安全 安全 安全 较安全 较安全 0.36~0.46 安全 安全 较安全 较安全 中等 0.46~0.56 安全 较安全 中等 中等 较危险 0.56~0.66 安全 中等 较危险 较危险 危险 0.66~0.84 安全 中等 较危险 危险 危险 注:Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ分别为导水裂隙带扰动破坏含水层距离<0 m、0~6 m、6~12 m、12~18 m、>18 m。 由图5可知:危险区主要集中在矿区中部呈条带状分布,这是该区域富水性较强与顶板隔水层较薄共同作用的结果,虽然矿区东北部富水性较好,但由于该区域冒裂安全性较低,因此,整体危险性较低;同理,西南区域富水性较弱,降低了较高采裂危险性带来的突水风险。
5. 结 语
1)基于实测样本,提出并构建LDA-RBF导水裂隙带发育高度预测模型,与传统RBF导水裂隙带模型相比,LDA-RBF结构简单但预测精度更高,平均相对误差为4.09%,确定龙凤煤矿9#煤层导水裂隙带预测高度为50.4 m。
2)根据预测结果,对比9#煤层顶板到含水层底界距离,得到龙凤煤矿冒裂安全性分区。结果表明:由于隔水层较薄,开采过程中大部分区域将超过含水层底界。
3)针对现有突水评价方法的自有局限性,引入并改进了CRITIC法,并结合层次分析法构建CRITIC-AHP综合赋权法评价含水层富水性,其评价结果与钻孔抽放水实验结果吻合,验证了该方法的合理性。
4)通过ArcGis绘制相关图层,并叠加采裂危险性分区图层与富水性分区图层,得到了龙凤煤矿9#煤层顶板突水危险性分区图,其危险区域主要在矿区中部呈条状分布并向四周过渡,矿区大部分区域突水危险性等级在过渡级以上,说明在实际开采过程中应对以上区域予以重视。
-
表 1 国内部分矿区导水裂隙带实测数据
Table 1 The measured data of water conducting fracture zone in some mining areas in China
编号 开采
深度/
m开采
厚度/
m工作面
斜长/
m煤层
倾角/
(°)顶板
类型Ⅲ导水裂隙
带高度/
m1# 89 2.00 114 7.0 Ⅰ 45.00 2# 117 3.40 205 2.0 Ⅲ 72.00 3# 89 2.03 69 7.0 Ⅱ 45.86 4# 282 4.00 71 8.0 Ⅲ 33.00 5# 328 2.00 78 7.0 Ⅱ 23.00 ︙ ︙ ︙ ︙ ︙ ︙ ︙ 30# 86 4.60 170 7.0 Ⅱ 53.00 31# 396 3.45 160 14.0 Ⅲ 26.70 32# 168 3.00 137 5.5 Ⅳ 27.50 表 2 LDA-RBF与RBF模型导水裂隙带高度实测值与预测值对比
Table 2 Comparison between the measured and predicted values of the height of water-conducting fracture zone in LDA-RBF and RBF models
样本
编号顶板
类型实测高度/
m预测高度/m 预测高度相对误差/% LDA-RBF RBF LDA-RBF RBF 29# 1 72.0 72.05 0.07 72.76 1.06 30# 2 53.0 50.18 5.32 42.08 20.60 31# 3 26.7 25.55 4.31 22.90 14.23 32# 4 27.5 25.67 6.65 30.12 9.52 表 3 因素间相关系数矩阵
Table 3 Matrix of correlation coefficient between factors
因素 含水层
厚度岩性结构
指数脆塑
性比岩心
采取率含水层厚度 1.000 0 −0.3515 0.5438 0.1004 岩性结构指数 −0.3515 1.000 0 0.3162 −0.2519 脆塑性比 0.5438 0.3162 1.000 0 −0.0914 岩心采取率 0.1004 −0.2519 −0.0941 1.000 0 表 4 相关系数修正矩阵
Table 4 Correlation coefficient correction matrix
因素 含水层
厚度岩性结构
指数脆塑性比 岩心
采取率含水层厚度 1 0 1 0 岩性结构指数 0 1 1 0 脆塑性比 1 1 1 0 岩心采取率 0 0 0 1 表 5 修正后相关系数矩阵
Table 5 Corrected correlation coefficient matrix
因素 含水层
厚度岩性结构
指数脆塑性比 岩心
采取率含水层厚度 1.000 0 0 0.543 8 0 岩性结构指数 0 1.000 0 0.316 2 0 脆塑性比 0.5438 0.312 6 1.000 0 0 岩心采取率 0 0 0 1 表 6 各主控因素权重值
Table 6 Weight value of each main control factor
权重 含水层
厚度岩性结构
指数脆塑
性比岩心
采取率CRITIC权重 0.29 0.27 0.20 0.24 AHP权重 0.37 0.21 0.23 0.19 CRITIC-AHP组合权重 0.33 0.24 0.22 0.21 表 7 顶板突水划分标准
Table 7 Roof water bursting risk evaluation standard
富水性指数顶板突水分区 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ 0.26~0.36 安全 安全 安全 较安全 较安全 0.36~0.46 安全 安全 较安全 较安全 中等 0.46~0.56 安全 较安全 中等 中等 较危险 0.56~0.66 安全 中等 较危险 较危险 危险 0.66~0.84 安全 中等 较危险 危险 危险 注:Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ分别为导水裂隙带扰动破坏含水层距离<0 m、0~6 m、6~12 m、12~18 m、>18 m。 -
[1] 史红邈,姚邦华,温志辉,等. 煤矿陷落柱突水主控因素研究[J]. 煤矿安全,2020,51(12):232−236. SHI Hongmiao, YAO Banghua, WEN Zhihui, et al. Study on main control factors for karst collapse column water inrush in coal mines[J]. Safety in Coal Mines, 2020, 51(12): 232−236.
[2] 李博,韦韬,刘子捷. 西南地区煤层顶板岩溶含水层富水性评价指标体系构建及突水危险性评价[J]. 煤炭学报,2022,47(S1):152−159. LI Bo, WEI Tao, LIU Zijie. Construction of evaluation index system for water abundance of karst aquifers and risk assessment of water inrush on coal seam roof in southwest China[J]. Journal of China Coal Society, 2022, 47(S1): 152−159.
[3] 龙良良,王生全,肖乐乐,等. 基于GIS的巨厚煤层顶板突水危险性预测[J]. 煤矿安全,2020,51(12):45−49. LONG Liangliang, WANG Shengquan, XIAO Lele, et al. Risk prediction of water inrush from roof of ultra thick coal seam based on GIS[J]. Safety in Coal Mines, 2020, 51(12): 45−49.
[4] 侯恩科,严迎新,文强,等. 巷道掘进顶板突水危险性预测研究[J]. 煤炭科学技术,2022,50(10):110−120. HOU Enke, YAN Yingxin, WEN Qiang, et al. Study on prediction of water inrush hazard in roof of roadwaydriving[J]. Coal Science and Technology, 2022, 50(10): 110−120.
[5] 周全超,张洪清,焦扬,等. 基于组合赋权法的煤层顶板突水危险性评价[J]. 科学技术与工程,2022,22(9):3497−3503. doi: 10.3969/j.issn.1671-1815.2022.09.011 ZHOU Quanchao, ZHANG Hongqing, JIAO Yang, et al. Evaluation of the risk of water inrush from coal roof based on combination weighting method[J]. Science Technology and Engineering, 2022, 22(9): 3497−3503. doi: 10.3969/j.issn.1671-1815.2022.09.011
[6] LIU Shiliang, LI Wenping. Fuzzy comprehensive risk evaluation of roof water inrush based on catastrophe theory in the Jassic coalfield of northwest China[J]. Journal of Intelligent & Fuzzy Systems, 2019(37): 2101−2111.
[7] XIE Daolei, HAN Jing, ZHANG Huide, et al. Risk assessment of water inrush from coal seam roof based on combination weighting set pair analysis[J]. Sustainability, 2022, 14(19): 11978. doi: 10.3390/su141911978
[8] 刘年平,赵春侠,王宏图,等. 煤层底板突水危险性的可拓聚类预测方法研究[J]. 矿业安全与环保,2016,43(2):63−66. doi: 10.3969/j.issn.1008-4495.2016.02.016 LIU Nianping, ZHAO Chunxia, WANG Hongtu, et al. Research on extension clustering prediction method for coal seam floor water inrush risk[J]. Mining Safety & Environmental Protection, 2016, 43(2): 63−66. doi: 10.3969/j.issn.1008-4495.2016.02.016
[9] 王心义,姚孟杰,张建国,等. 基于改进AHP法与模糊可变集理论的煤层底板突水危险性评价[J]. 采矿与安全工程学报,2019,36(3):558−565. WANG Xinyi, YAO Mengjie, ZHANG Jianguo, et al. Evaluation of water bursting in coal seam floor based on improved AHP and fuzzy variable set theory[J]. Journal of Mining & Safety Engineering, 2019, 36(3): 558−565.
[10] 尹尚先,徐维,尹慧超,等. 深部开采底板厚隔水层突水危险性评价方法研究[J]. 煤炭科学技术,2020,48(1):83−89. YIN Shangxian, XU Wei, YIN Huichao, et al. Study on risk assessment method of water inrush from thick floor aquifuge in deep mining[J]. Coal Science and Technology, 2020, 48(1): 83−89.
[11] 盖秋凯,黄磊,赵霖. 基于因子分析法的焦作矿区底板突水模型研究[J]. 煤炭工程,2021,53(1):123−127. GAI Qiukai, HUANG Lei, ZHAO Lin. Floor water inrush model of Jiaozuo mining area based on factor analysis[J]. Coal Engineering, 2021, 53(1): 123−127.
[12] 武强,黄晓玲,董东林,等. 评价煤层顶板涌(突)水条件的“三图-双预测法”[J]. 煤炭学报,2000(1):60−65. doi: 10.3321/j.issn:0253-9993.2000.01.014 WU Qiang, HUANG Xiaoling, DONG Donglin, et al. “Three maps two predictions” method to evaluate water bursting coditions on roof coal[J]. Journal of China Coal Society, 2000(1): 60−65. doi: 10.3321/j.issn:0253-9993.2000.01.014
[13] WU Qiang, SHEN Jianjun, LIU Weitao, et al. A RBFNN-based method for the prediction of the developedheight of a water-conductive fractured zone for fullymechanized mining with sublevel caving[J]. Arabian Journal of Geosciences, 2010(7): 172.
[14] 郭均中. 上覆岩层导水裂隙带发育高度预测研究[D]. 三河:华北科技学院,2018. [15] 李振华,许延春,李龙飞,等. 基于BP神经网络的导水裂隙带高度预测[J]. 采矿与安全工程学报,2015,32(6):905−910. LI Zhenhua, XU Yanchun, LI Longfei, et al. Forecast of the height of water flowing fractured zone based on BP neural networks[J]. Journal of Mining & Safety Engineering, 2015, 32(6): 905−910.
[16] 施龙青,吴洪斌,李永雷,等. 导水裂隙带发育高度预测的PCA-GA-Elman优化模型[J]. 河南理工大学学报(自然科学版),2021,40(4):10−18. SHI Longqing, WU Hongbin, LI Yonglei, et al. Optimization model of PCA-GA-Elman for development height prediction of water-conducting fissure zone[J]. Journal of Henan Polytechnic University (Natural Science), 2021, 40(4): 10−18.
[17] BI Yaoshan, WU Jiwen, ZHAI Xiaorong, et al. A prediction model for the height of the water-conducting fractured zone in the roof of coal mines based on factoranalysis and RBF neural network[J]. Arabian Journal ofGeosciences, 2022, 15(3): 241. doi: 10.1007/s12517-022-09523-3
[18] 赵德星. 基于Elman神经网络的导水裂隙带高度预测模型[J]. 山西煤炭,2022,42(2):8−14. doi: 10.3969/j.issn.1672-5050.2022.02.002 ZHAO Dexing. Prediction model for height of water flowing fractured zones based on Elman neural network[J]. Shanxi Coal, 2022, 42(2): 8−14. doi: 10.3969/j.issn.1672-5050.2022.02.002
[19] 姚文涛,寇天昊,樊斌,等. 采动覆岩离层注浆对矿井安全的影响评价[J]. 煤炭技术,2022,41(8):170−174. YAO Wentao, KOU Tianhao, FAN Bin, et al. Influence evaluation of mining-induced strata separation grouting on mine safety[J]. Coal Technology, 2022, 41(8): 170−174.
[20] 武强,许珂,张维. 再论煤层顶板涌(突)水危险性预测评价的“三图-双预测法”[J]. 煤炭学报,2016,41(6):1341−1347. WU Qiang, XU Ke, ZHANG Wei. Further research on “three maps-two predictions” method for prediction on coalseam roof water bursting risk[J]. Journal of China Coal Society, 2016, 41(6): 1341−1347.
[21] 王晓振,许家林,韩红凯,等. 顶板导水裂隙高度随采厚的台阶式发育特征[J]. 煤炭学报,2019,44(12):3740−3749. WANG Xiaozhen, XU Jialin, HAN Hongkai, et al. Stepped development characteristic of water flowing fracture heightwith variation of mining thickness[J]. Journal of China Coal Society, 2019, 44(12): 3740−3749.
[22] 郭文兵,娄高中. 覆岩破坏充分采动程度定义及判别方法[J]. 煤炭学报,2019,44(3):755−766. GUO Wenbing, LOU Gaozhong. Definition and distinguishing method of critical mining degree of overburden failure[J]. Journal of China Coal Society, 2019, 44(3): 755−766.
[23] 李哲,陈嘉思,宫厚健,等. 煤层直接顶板弱富水性含水层涌(突)水危险性评价[J]. 煤矿安全,2018,49(7):181−184. LI Zhe, CHEN Jiasi, GONG Houjian, et al. Risk evaluation of water inrush in poor water yield capacity aquifer of coal seam direct roof[J]. Safety in Coal Mines, 2018, 49(7): 181−184.
[24] SUN Zhenming, BAO Wenpeng. Comprehensive water inrush risk assessment method for coal seam roof[J]. Stainability, 2022, 14(17): 10475. doi: 10.3390/su141710475
[25] 肖乐乐,牛超,代革联,等. 基于富水性结构指数法的直罗组地层富水性评价[J]. 煤炭科学技术,2018,46(11):207−213. XIAO Lele, NIU Chao, DAI Gelian, et al. Evaluation of water abundance in Zhiluo formation based watery structure index method[J]. Coal Science and Technology, 2018, 46(11): 207−213.
[26] 薛建坤. 基于分形理论的富水性指数法在含水层富水性评价中的应用[J]. 煤矿安全,2020,51(2):197−201. XUE Jiankun. Application of water-rich index method based on fractal theory in water-rich evaluation of aquifer[J]. Safety in Coal Mines, 2020, 51(2): 197−201.
[27] LI Ruipeng, ZHENG Lulin, Xie Jin, et al. Assessment of water inrush from coal floor based on karst fractal-vulnerability index method[J]. Mathematical Problems in Engineerig, 2022(8): 1−12.
-
期刊类型引用(1)
1. 范铭今,陈军涛,古海龙,唐道增,韩港,张树强,李光强. 西部矿区可注断层破碎带注浆加固特性试验研究. 煤矿安全. 2025(01): 155-163 .  本站查看
本站查看
其他类型引用(0)




 下载:
下载: