Mechanical properties and energy dissipation law of saturated coal samples under dynamic loading
-
摘要:
为探究饱水煤样在动态加载下的力学特性和能量变化特征，采用直径50 mm的分离式霍普金森杆装置（SHPB）对饱水和自然状态2种煤样开展冲击加载试验，分析含水状态对煤样的动态强度、应变、损伤和能量传递效率的影响。结果表明：在应变率14.25~59.57 s−1内，水体对煤样动态强度具有双重作用，表现为低应变率弱化和高应变率强化；相同冲击载荷下，自然、饱水煤的变形差异显著，最大应变相差38.46%；煤样含水状态显著影响能量传递效率，其中自然和饱水煤样的能耗密度均与入射能呈线性增长关系，且自然煤能量反射率大于饱水煤能量反射率，自然煤透射率小于饱水煤透射率，耗散率二者近似相等。
Abstract:To investigate the mechanical properties and energy variation characteristics of saturated coal samples under dynamic loading, a 50 mm diameter split Hopkinson rod device (SHPB) was used to conduct impact loading tests on both saturated and natural coal samples, and to analyze influence of water content on the dynamic strength, strain, damage, and energy transfer efficiency of coal samples. The results show that within the strain rate range of 14.25 s−1 to 59.57 s−1, water has a dual effect on the dynamic strength of coal samples, manifested as low strain rate weakening and high strain rate strengthening; under the same impact load, there is a significant difference in deformation between natural coal and saturated coal, with a maximum strain difference of 38.46%; the water content of coal samples significantly affects the energy transfer efficiency, where the energy consumption density of both natural and saturated coal samples increases linearly with incident energy, and the energy reflectance of natural coal is more than that of saturated coal, and the transmittance of natural coal is less than that of saturated coal, and the dissipation rate is approximately equal.
-
煤炭是我国主要能源和重要的工业原料，煤炭安全稳定供应关系到国民经济发展全局，但煤矿瓦斯灾害长期制约着煤炭产业健康发展[1-3]。长钻孔是治理瓦斯的有效手段之一，与传统钻孔方式相比较，具有抽采体积分数大、抽放时间长等优点[4-7]。但并非钻孔长度越长，瓦斯抽采效果越好。由于钻孔长度过长，在瓦斯流动过程中存在负压衰减现象，对钻孔周围瓦斯流动造成影响，进而影响瓦斯连续高效抽采，造成残余瓦斯分布不均[8-9]。因此，研究负压衰减效应下长钻孔抽采时的煤层残余瓦斯分布规律具有重要意义。
众多学者对这一问题进行了大量研究，取得了较为丰富的研究成果。江成等[10]分析了抽采过程邻近层瓦斯压力演化与煤层变形关系，得出邻近层瓦斯压力衰减呈近似直线；李路广等[11]为了提高矿井瓦斯抽采钻孔施工效率和煤层瓦斯的抽采效果，依据千米定向钻机轨迹可控、过程可溯的特点，通过工业试验实现了对煤与瓦斯突出风险的有效管控，提高了瓦斯抽采效率；冀超辉等[12]在乌冬煤矿进行了特厚急倾斜煤层抽采应用，建立了一套针对特厚急倾斜煤层瓦斯抽采技术；翟成等[13]在祁东煤矿采用高位钻孔抽放技术解决了瓦斯超限问题；毕慧杰等[14]采用理论计算和数值模拟的方法研究了采动裂隙演化规律，计算出合理的施工位置，达到提高了抽采纯量的效果；李宏等[15]为进一步提高采空区裂隙带瓦斯抽采效率，提出了一种大直径顶板定向长钻孔瓦斯抽采技术，取得了经济、高效的现场应用效果；王广宏[16]根据榆树田煤矿实际情况建立抽采流固模型，分析了钻孔负压、长度等钻孔参数对瓦斯抽采的影响；徐超等[17]基于COMSOL数值模拟软件和理论计算方法，建立煤层瓦斯扩散—渗流模型，分析了钻孔内各区段沿程阻力损失和抽采钻孔内负压衰减的影响因素；王兆丰等[18]、李杰[19]、宋建军[20]通过理论分析和现场试验，对顺层钻孔孔内负压分布规律也开展了大量的研究工作。
综上所述，目前针对负压衰减效应下长钻孔抽采时煤层瓦斯残余量分布规律的研究较少。因此，采用数值模拟方法，结合瓦斯-空气模型与钻孔负压衰减方程，阐明长钻孔抽采下煤层残余瓦斯分布规律，以期为优化瓦斯抽采钻孔布置、提高瓦斯抽采效率等方面提供理论支撑。
1. 长钻孔瓦斯抽采模型
1.1 渗透率和孔隙率方程
在理想状态煤体内部瓦斯压力下降，煤体基质将会产生收缩变形，煤体孔隙体积增大。根据相关研究可知，煤体发生瓦斯解吸收缩应变εp计算如下[21]：
$$ {\varepsilon _p} = \frac{{4ac{\rho _{\mathrm{v}}}RT}}{{9{V_{\mathrm{m}}}{K_{\mathrm{m}}}}}\ln \left( {1 + b{p_{\mathrm{m}}}} \right) $$ (1) 式中：a为吸附常数，m3/t；b为吸附常数，MPa−1；c为煤可燃部分质量，kg；ρv为煤的视密度，kg/m3；R为理想气体常数；T为温度，K；Vm为标准气体摩尔体积，L/mol；Km为基质弹性模量，GPa；pm为煤基质瓦斯压力，MPa。
煤体基质吸收瓦斯收缩变形为可逆过程，当煤体瓦斯压力由初始瓦斯压力p0降至pm，基质收缩应变$ \Delta {\varepsilon _p} $为：
$$ \Delta {\varepsilon _p} = {\varepsilon _{{p_0}}} - {\varepsilon _{{p_{\text{m}}}}} = \frac{{4ac{\rho _{\mathrm{v}}}RT}}{{9{V_{\mathrm{m}}}{K_{\mathrm{m}}}}}\ln \left( {\frac{{1 + b{p_0}}}{{1 + b{p_{\mathrm{m}}}}}} \right) $$ (2) 式中：$ {\varepsilon _{p_0}} $为初始应变；$ {\varepsilon _{p_{\mathrm{m}}}} $为压力为pm时的应变。
假设瓦斯解吸不影响煤体体积，将式（2）代入孔隙率计算公式，得到瓦斯解吸后煤体孔隙率φm为：
$$ {\varphi _{\mathrm{m}}} = {\varphi _0} + \Delta {\varepsilon _p} = {\varphi _0} + \frac{{4ac{\rho _{\mathrm{v}}}RT}}{{9{V_{\mathrm{m}}}{K_{\mathrm{m}}}}}\ln \left( {\frac{{1 + b{p_0}}}{{1 + b{p_{\mathrm{m}}}}}} \right) $$ (3) 式中：φ0为初始孔隙率。
Kozeny-Carman方程关于孔隙率与渗透性的方程为[22]：
$$ k = \frac{{\rho g{d^2}{\varphi ^3}}}{{180\mu {{\left( {1 - \varphi } \right)}^2}}} $$ (4) 式中：k为动态渗透率，m²；g为重力常量，m/s²；ρ为煤的密度，kg/m³；d为固体颗粒平均直径，m；μ为气体黏度，Pa·s；$\varphi $为孔隙率。
将式（3）代入式（4）可以得到基质渗透率km为：
$$ {k_{\mathrm{m}}} = {k_0}{\left\{ {1 + \frac{{4ac{\rho _{\mathrm{v}}}RT}}{{9{V_{\mathrm{m}}}{K_{\mathrm{m}}}}}\ln \left( {\frac{{1 + b{p_0}}}{{1 + b{p_{\mathrm{m}}}}}} \right)} \right\}^3} $$ (5) 式中：k0为初始渗透率，m2。
1.2 渗透率动态演化方程
考虑有效应力对孔隙率的影响，双重介质中的孔隙率表达式可定义为：
$$ {\varphi _{\mathrm{m}}} = \frac{{{V_{\mathrm{p}}}}}{{{V_{\mathrm{t}}}}} = \frac{{{V_{{\mathrm{p}}0}} - \Delta V}}{{{V_{{\mathrm{t}}0}} - \Delta V}} = \frac{{{\varphi _0} - {\varepsilon _{\mathrm{v}}}}}{{1 - {\varepsilon _{\mathrm{v}}}}} $$ (6) 式中：Vp为煤变形前后的孔隙体积，m3；Vt为孔隙体积，m3；Vp0为煤变形前的孔隙体积，m3；Vt0为初始孔隙体积，m3；ɛv为体积应变；ΔV为孔隙体积变化量，m3。
煤体瓦斯压力由p0降至p1，空气压力由0升至p2，将应变代入式（5），得到多孔介质孔隙变化方程：
$$ \begin{split} & \begin{gathered} \varphi = {\varphi _0} - \frac{{a\left( {1 - {\varphi _0}} \right)\left( {{p_0} - {p_1} + {p_2}} \right)}}{{{K_{\mathrm{f}}} - a\left( {{p_0} - {p_1} + {p_2}} \right)}} +\\ \frac{{4ac{\rho _{\mathrm{v}}}RT\left[ {\ln \left( {1 + b{p_0}} \right) - \ln \left( {1 + b{p_{\mathrm{m}}}} \right)} \right]}}{{9{V_{\mathrm{m}}}{K_{\mathrm{m}}}\left[ {{K_{\mathrm{f}}} - a\left( {{p_0} - {p_1} + {p_2}} \right)} \right]}} \end{gathered} \\[-14pt]& \end{split} $$ (7) 考虑基质收缩与有效应力，得到基质渗透率动态演化方程：
$$\begin{split} & \begin{gathered} k = {k_0}{\left( {\frac{\varphi }{{{\varphi _0}}}} \right)^3} = {k_0}\left\{ {1 - \frac{{a\left( {1 - {\varphi _0}} \right)\left( {{p_0} - {p_1} + {p_2}} \right)}}{{{K_{\mathrm{f}}} - a\left( {{p_0} - {p_1} + {p_2}} \right)}}}+ \right. \\ {\left. { \frac{{4ac{\rho _{\mathrm{v}}}RT\left[ {\ln \left( {1 + b{p_0}} \right) - \ln \left( {1 + b{p_{\mathrm{m}}}} \right)} \right]}}{{9{V_{\mathrm{m}}}{K_{\mathrm{m}}}\left[ {{K_{\mathrm{f}}} - a\left( {{p_0} - {p_1} + {p_2}} \right)} \right]}}} \right\}^3} \end{gathered} \\[-14pt] & \end{split} $$ (8) 1.3 瓦斯流动方程
瓦斯−空气双气体系统中，只考虑气体在多孔介质扩散，控制方程与单一气体在多孔物质相似。其物质交换方程可表示为[23]：
$$ {Q_{\mathrm{m}}} = {D_t}\tau \left( {{c_{\mathrm{m}}} - {\rho _{\mathrm{f}}}} \right) = {D_t}\frac{{3{\pi ^2}}}{{{L^2}}}\left( {{c_{\mathrm{m}}} - {\rho _{\mathrm{f}}}} \right) $$ (9) 式中：Qm为基质与孔隙裂隙的气体交换量，m³/s；Dt为流体扩散系数，m2/s；τ为形状因子；cm、ρf分别为基质与孔隙裂隙中的流体密度，kg/m3；L为基质的孔径，m。
流体扩散系数可表示为：
$$ {D_t} = {D_0}{{\mathrm{e}}^{ - \xi t}} + {D_{\mathrm{r}}} $$ (10) 式中：D0为气体初始扩散系数，m2/s；ξ为衰减系数；t为时间，s；Dr为剩余气体扩散系数，m2/s。
将气体压强公式与式(10)代入式(9)，得到质量交换方程的控制方程：
$$ {Q_{\mathrm{m}}} = \frac{{3{\pi ^2}{M_{\mathrm{c}}}\left( {{p_{\mathrm{n}}} - {p_{\mathrm{f}}}} \right)\left[ {{D_0}{{\mathrm{e}}^{ - \xi t}} + {D_{\mathrm{r}}}} \right]}}{{{L^2}RT}} $$ (11) 式中：Mc为甲烷摩尔质量，kg/mol；pn为基质中流体压力，MPa；pf为孔隙中流体压力，MPa。
单位质量煤基质含气量可表示为：
$$ {m_{\mathrm{p}}} = \frac{{abp\rho {M_{\mathrm{c}}}}}{{\left( {1 + bp} \right){V_{\mathrm{m}}}}} + {\varphi _{\mathrm{p}}}\frac{{{M_{\mathrm{c}}}p}}{{RT}} $$ (12) 将式（10）和式（11）代入质量守恒方程得到煤体裂隙瓦斯压力分布方程，即：
$$ \begin{split} & \begin{gathered} \frac{\partial }{{\partial t}}\left( {\frac{{{M_{\mathrm{c}}}{\rho _{\mathrm{c}}}}}{{{V_{\mathrm{m}}}}} \cdot \frac{{{V_{\mathrm{L}}}{p_{\mathrm{m}}}}}{{{p_{\mathrm{L}}} + {p_{\mathrm{m}}}}} + \phi m\frac{{{M_{\mathrm{c}}}{p_{\mathrm{m}}}}}{{RT}}} \right)= \\ - \frac{{3{\pi ^2}{M_{\mathrm{c}}}\left( {{p_{\mathrm{m}}} - {p_{\mathrm{f}}}} \right)\left[ {{D_0}{{\mathrm{e}}^{ - \xi t}} + {D_{\mathrm{r}}}} \right]}}{{{L^2}RT}} \end{gathered} \\[-14pt]& \end{split} $$ (13) 1.4 煤变形方程
随着埋深的增加，煤体受到地应力与瓦斯压力共同作用。煤体变形方程可用Navier-Stokes方程表示[24]：
$$ G{u_{i,jj}} + \frac{G}{{1 - 2v}}{u_{j,ji}} - {\alpha _{\mathrm{m}}}{p_{\mathrm{m}}} - {k_{\mathrm{f}}}{\varepsilon _{s,i}} + {F_i} = 0 $$ (14) 式中：G为剪切模量，G=E/2(1+υ)，GPa；E为弹性模量，GPa；υ为泊松比；kf为裂隙的Biot’s系数；αm为煤基质的Biot’s系数；εs,i为基质最大应变；Fi为体积力分量。
1.5 压损计算
假设钻孔全部处于煤体中，为方便分析，沿着钻孔长度方向将钻孔分割为若干个控制单元，顺层钻孔控制单元示意图如图1所示。
钻孔中煤体压力损失由沿程阻力损失和压降损失组成，其中压降损失由加速度压降和局部压降组成，沿程损失是由流体流动与管道壁面形成的阻力；加速度压降是抽采过程流体质量不断变化，当截面相同，流体流量越大，速度越大。在速度增加过程中伴随部分能量损失；局部压降是由钻孔内部截面发生变化形成是能量损失，如钻孔变形，塌孔等。其理论控制单元压力损失公式为[23]：
$$ \begin{split} & \begin{gathered} \frac{{{\mathrm{d}}p\left( x \right)}}{{{\mathrm{d}}x}} = \Delta {p_{{\mathrm{yc}}}} + \Delta {p_{{\mathrm{yj}}}} = \frac{{2{f_i}\rho {{\left[ {2Q\left( x \right) + q\left( x \right)} \right]}^2}}}{{{\pi ^2}{D^5}}}+ \\ \frac{{16\rho \left[ {{q^2}\left( x \right) + 2Q\left( x \right)q\left( x \right)} \right]}}{{{\pi ^2}{D^4}}} \end{gathered} \\[-14pt]& \end{split} $$ (15) 式中：pyc为钻孔沿程阻力损失；pyj为钻孔压降；p(x)为距离孔口x处钻孔内部气体压力，MPa；q(x)为距离孔口x处瓦斯涌出量，m³；Q(x)为距离孔口x处钻孔内瓦斯气体流量，m3/s；x为距孔口距离，m；fi为孔壁摩擦修正系数；D为钻孔直径，m。
2. 钻孔附近残余瓦斯分布
钻孔周围煤体残存瓦斯含量与煤层瓦斯压力存在对应关系，而煤体瓦斯压力与煤体受到的压力差有关。越靠近钻孔煤体瓦斯与钻孔形成的压力差越大，煤体瓦斯降低越多，使得煤体吸附-解吸平衡破坏，更多吸附瓦斯解吸为游离瓦斯，煤体瓦斯含量降低。因此，在钻孔横截面瓦斯呈对数函数趋势。由于钻孔存在抽采负压衰减现象，孔口抽采负压低于孔底，因此理论分析钻孔深度残余瓦斯含量也呈现对数函数分布。钻孔附近残余瓦斯含量示意图如图2所示。
3. 煤层残余瓦斯含量模拟
3.1 模型建立和边界条件设置
为了研究负压衰减效应下抽采长钻孔残余瓦斯分布规律，根据工程地质背景，建立数值模型。三维模型尺寸为60 m×300 m ×11 m（宽×深×高），其中，中间层设置3 m厚煤层，在煤层的顶部设置4 m厚顶板，底部设置4 m厚底板。在模型内部x方向14 m处，开挖1条巷道；巷道沿y轴开挖，巷道长60 m，宽4 m。沿x轴在巷道中部设置钻孔，钻孔初始长度为150 m，直径为37.5 mm。模型网格划分示意图如图3所示。
由于贵州地区地表地貌不平整，不同位置上覆岩层厚度不同，受到的垂直应力也不同，为了简化计算，上覆岩层厚度取研究巷道埋深平均值。整个模型采用自由四面体进行划分，选择与达西定律和一般形式偏微分方程的2个物理场初始设置值一致，根据岩层密度简易计算出应在模型上方施加8 MPa垂直应力，模型下方采用固定约束，四周指定位移方向并施加3 MPa水平应力，巷道内部采用自由边界。初始模型中设置20 m为钻孔封孔长度，封孔材料膨胀后将对钻孔周围施加应力，因此在该位置钻孔受到1.5 MPa封孔压力，其余抽采段钻孔周围采用自由边界，并施加13 kPa抽采负压。瓦斯抽采模型参数见表1。
表 1 瓦斯抽采模型参数表Table 1. Gas extraction model parameters table输入参数 数值 输入参数 数值 初始孔隙率/% 3 初始渗透率/m2 1.189 9×10−17 煤密度/（kg·m−3） 1 400 瓦斯动力黏度/（Pa·s） 1.05×10−6 煤的泊松比 0.29 初始瓦斯压力/MPa 1.4 煤弹性模量/MPa 2 713 煤层温度/K 293.15 初始瓦斯扩散系数/
（m2·s−1）5.48×10−12 煤体骨架
弹性模量/MPa5 139 吸附常数b/MPa−1 2 吸附常数a/（m3·t−1） 35 3.2 数值模拟结果
不同抽采时间煤体残余瓦斯含量如图4所示，各时间段延钻孔长度方向煤层残存瓦斯含量曲线如图5所示。
![]()
图 4 不同抽采时间煤体残余瓦斯含量Figure 4. Residual gas content of coal body at different extraction times![]()
图 5 各时间段延钻孔长度方向煤层残存瓦斯含量曲线Figure 5. Curves of residual gas content in coal seams with drilling length at different time periods由数值模拟结果可知，随着抽采不断进行，钻孔周围瓦斯含量不断降低，并且范围不断扩大。观测各图钻孔处瓦斯含量，钻孔孔口处瓦斯含量要低于孔底，并且越到抽采后期越明显。这是由于钻孔内部负压受到衰减作用，负压分布不是均匀的，越靠近孔底负压衰减越多，最终造成孔底瓦斯残余含量高于孔口。
3.3 沿钻孔走向残余瓦斯分布
不同测线瓦斯残余含量如图6所示。由图6可知，随着抽采的进行，钻孔附近瓦斯含量不断降低，钻孔深部瓦斯含量也存在降低现象。钻孔初期，抽采段初始位置瓦斯含量与其他位置相差不大，但在抽采后期差距不断增大。由于在封孔段末端煤体受到封孔材料压力，使得煤体压实，孔隙率减小，瓦斯在附近运移更加困难，瓦斯流动阻力增大，使得封孔段末端含量变化存在“滞后”现象。
通过前面理论分析可知，在长钻孔抽采过程存在抽采负压衰减现象，在短钻孔抽采过程中，负压衰减引起的瓦斯残存量差异较小，当钻孔深度达到一定长度时抽采负压衰减成为不可忽略的因素。抽采钻孔由于孔壁的粗糙性以及钻孔不断流入钻孔瓦斯等因素影响，越靠近孔底抽采负压损失越大，由于抽采动力由负压及煤层压力共同决定。根据现场实际工程情况，煤层压力在同一区域内变化不大，因此抽采负压衰减影响抽采效果。靠近封孔段瓦斯损失越小，压力梯度越大，影响范围越广。
4. 现场试验
试验选取在贵州林华煤矿进行，该矿位于贵州省金沙县西部，9#煤层位于龙潭组的中部，上段的底部，层位稳定，是井田内厚度最大的中厚煤层，区内主要可采煤层，硫分低，为优质无烟煤，9#煤层平均厚度为2.98 m。为验证模拟抽采后煤体残余瓦斯分布趋势，在该煤矿20915瓦斯治理专用巷瓦斯抽采达标位置钻取2个钻孔，分别测试钻孔40、50、60 m处瓦斯含量，共钻取1#、2# 2个取样孔，取样孔距离抽采孔0.5 m左右，为防止2个取样孔距离太近造成的测试误差，2个取样孔间距为10 m。取样过程采用ZDY4200钻机，配合使用96 mm钻头，取样过程采用风排渣，按照井下瓦斯含量测定要求严格控制取样时间。不同取样深度残余瓦斯含量如图7所示。
由图7可知，随着取样深度的增加，煤层瓦斯残余含量也随之增加。其中，1#钻孔在深度为40~60 m处，残余瓦斯含量在3.95~4.3 m3/t之间；2# 钻孔在深度为40~60 m处，残余瓦斯含量在4.3~5.7 m3/t之间；2个钻孔的残余瓦斯含量呈对数函数分布，1# 钻孔取样深度与残余量关系为y=
1.0373 ln(x)+0.2708 ，拟合度达到0.943 0；2# 钻孔取样深度与残余瓦斯含量关系为y=2.9321 ×ln(x)−6.5214 ，拟合度达到0.9572 。现场测试数据与模拟数据存在一定差异，是由于实际情况影响钻孔抽采因素过多，模拟过程忽略了部分因素，并且实际抽采过程负压不断变化，各支管负压也不相同，最终使得各位置残余瓦斯含量不同。总体而言，现场实测结果与理论分析结果相吻合。5. 结 语
1）钻孔横截面残余瓦斯呈对数函数趋势。由于钻孔存在抽采负压衰减现象，孔口抽采负压低于孔底，因此理论分析钻孔深度残余瓦斯含量也呈现对数函数分布。
2）由数值模拟可知，在封孔段末端煤体受到封孔材料压力，使得煤体压实，孔隙率减小，瓦斯在附近运移更加困难，瓦斯流动阻力增大，使得封孔段末端含量变化存在“滞后”现象。
3）现场实测结果表明，钻孔取得的残余瓦斯含量呈对数函数分布，1#钻孔取样深度与残余量关系为y=
1.0373 ln(x)+0.1708 ，拟合度达到0.9430 ；2#钻孔取样深度与残余量关系为y=2.9321 ln(x)−6.5214 ，拟合度达到0.9572 ，与理论分析结果相吻合。 -
![]()
图 4 饱水煤与自然煤动态抗压强度−应变率特征
Figure 4. Dynamic compressive strength strain rate characteristics of saturated coal and natural coal
![]()
图 9 不同状态煤样入射能与能耗密度关系图
Figure 9. Relation between incident energy and energy consumption density of coal samples in different states
![]()
图 10 不同含水状态煤样能量变化率
Figure 10. Energy change rate of coal samples with different water content conditions
表 1 煤样基本物理力学参数
Table 1 Basic physical and mechanical parameters of coal samples
密度/
(kg·m−3)弹性
模量/
GPa泊松比 单轴抗压
强度/
MPa单轴抗拉
强度/
MPa弹性能量
指数1 520 1.76 0.25 28.45 1.92 12.14 
下载: 导出CSV
表 2 动态加载下自然煤和饱水煤力学结果汇总
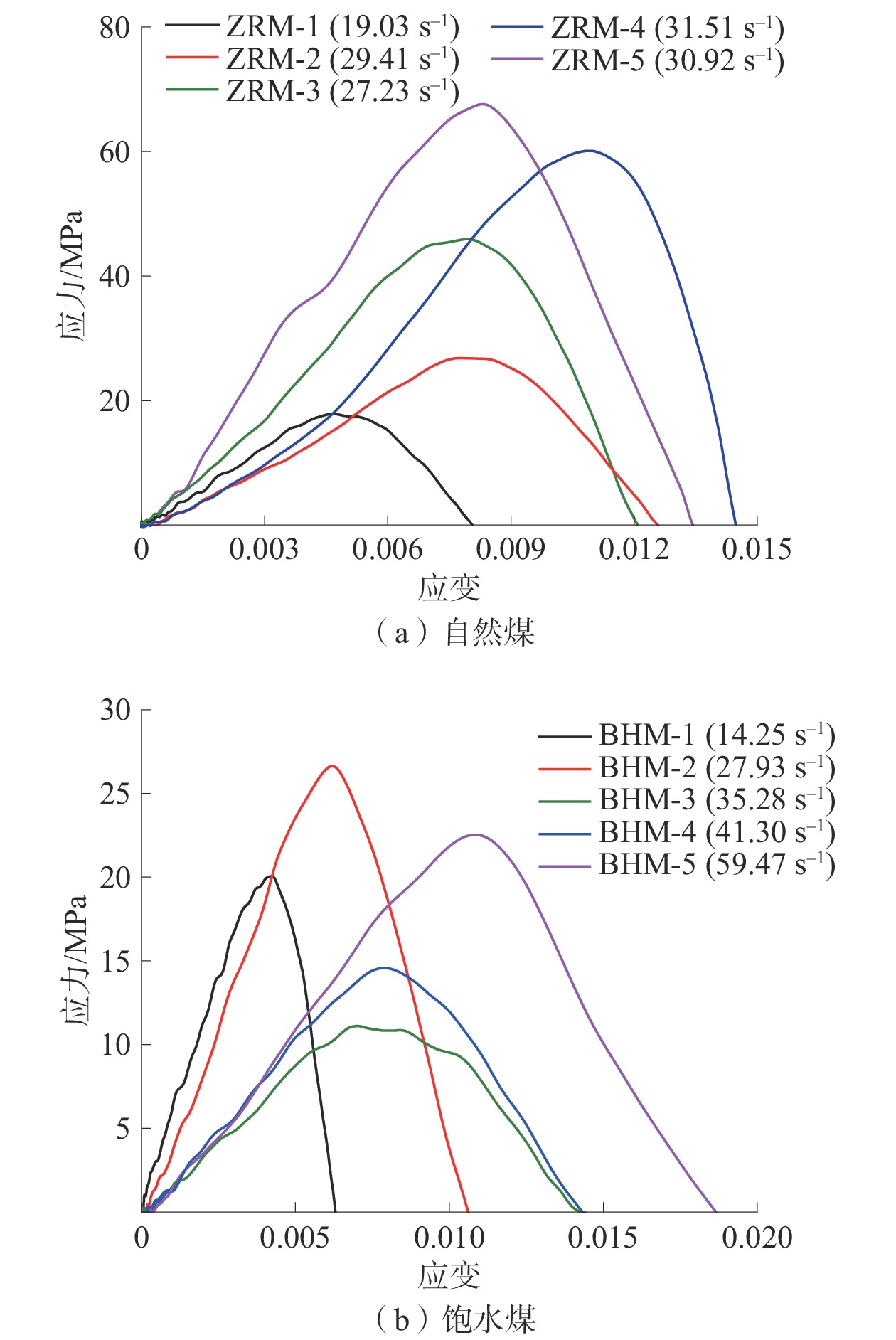
Table 2 Summary of mechanical results of natural coal and saturated coal under dynamic loading
煤样
状态煤样
编号冲击气压/
MPa冲击速度/
(m·s−1)应变率/
s−1抗压强度/
MPa弹性模量/
GPa自然煤 ZRM-1 0.1 3.76 19.03 18.46 3.98 ZRM-2 0.1 5.30 29.41 27.70 3.15 ZRM-3 0.1 6.00 27.23 46.64 6.06 ZRM-4 0.1 6.59 31.51 60.73 4.84 ZRM-5 0.1 8.00 30.92 68.51 9.37 饱水煤 BHM-1 0.1 3.84 14.25 20.41 5.56 BHM-2 0.1 5.30 27.93 26.63 4.59 BHM-3 0.1 6.01 35.28 11.66 1.60 BHM-4 0.1 7.15 41.30 15.06 1.99 BHM-5 0.1 7.46 59.47 22.53 2.19
下载: 导出CSV
-
[1] 蔡国军,程宇航,仲闯,等. 千枚岩饱水状态下软化效应试验分析[J]. 科学技术与工程,2021,21(8):3032−3038. CAI Guojun, CHENG Yuhang, ZHONG Chuang, et al. Experimental on softening effect of phyllite in saturated water[J]. Science Technology and Engineering, 2021, 21(8): 3032−3038.
[2] 郭军,冯国瑞,郭育霞,等. 饱和水煌斑岩单轴压缩力学特性变化及其微观机理[J]. 煤炭学报,2015,40(2):323−330. GUO Jun, FENG Guorui, GUO Yuxia, et al. Mechanical property variation under dynamic uniaxial compression and micro-mechanism of lamprophyre in saturated state[J]. Journal of China Coal Society, 2015, 40(2): 323−330.
[3] 王斌,李夕兵,尹土兵,等. 饱水砂岩动态强度的SHPB试验研究[J]. 岩石力学与工程学报,2010,29(5):1003−1009. WANG Bin, LI Xibing, YIN Shibing, et al. Split Hopkinson pressure bar (SHPB) experiments on dynamic strength of water-saturated sandstone[J]. Chinese Journal of rock mechanics and engineering, 2010, 29(5): 1003−1009.
[4] 王斌,李夕兵. 单轴荷载下饱水岩石静态和动态抗压强度的细观力学分析[J]. 爆炸与冲击,2012,32(4):423−431. WANG Bin, LI Xibing. Mesomechanics analysis of static compressive strength and dynamic compressive strength of water-saturated rock under uniaxial load[J]. Explosion and Shock Waves, 2012, 32(4): 423−431.
[5] HUANG Sheng, XIA Kaiwen, YAN Fei, et al. An experimental study of the rate dependence of tensile strength softening of Longyou sandstone[J]. Rock Mechanics and Rock Engineering, 2010, 43: 677−683. doi: 10.1007/s00603-010-0083-8
[6] 张亚宾,周建,艾蕊,等. 冲击载荷下石灰石力学特性与能耗规律研究[J]. 工程爆破,2022,28(2):15−20. ZHANG Yabin, ZHOU Jian, AI Rui, et al. Study on mechanical properties and energy consumption law of limestone under impact load[J]. Engineering Blasting, 2022, 28(2): 15−20.
[7] 赵立财. 饱水砂岩力学性质软化试验研究[J]. 地下空间与工程学报,2022,18(1):154−162. ZHAO Licai. Experimental study on mechanical property softening of water saturated sandstone[J]. Chinese Journal of Underground Space and Engineering, 2022, 18(1): 154−162.
[8] 郑广辉,许金余,王鹏,等. 水-岩耦合作用下红砂岩应变率效应研究[J]. 地下空间与工程学报,2017,13(1):79−85. ZHENG Guanghui, XU Jinyu, WANG Peng, et al. Research on strain rate effects of red-sandstone under water-rock coupling[J]. Chinese Journal of Underground Space and Engineering, 2017, 13(1): 79−85.
[9] 王凯,蒋一峰,徐超. 不同含水率煤体单轴压缩力学特性及损伤统计模型研究[J]. 岩石力学与工程学报,2018,37(5):1070−1079. WANG Kai, JIANG Yifeng, XU Chao. Mechanical properties and statistical damage model of coal with different moisture contents under uniaxial compression[J]. Chinese Journal of rock mechanics and engineering, 2018, 37(5): 1070−1079.
[10] 陈同庆,沈荣喜,李红儒,等. 自然和饱水煤样巴西劈裂过程声发射幅频特征试验[J]. 工矿自动化,2019,45(12):40−44. CHEN Tongqing, SHEN Rongxi, LI Hongru, et al. Experiment of amplitude and frequency feature of acoustic emission during Brazilian splitting testing of natural and saturated coal samples[J]. Industry and Mine Automation, 2019, 45(12): 40−44.
[11] 王文,李化敏,袁瑞甫,等. 动静组合加载含水煤样的力学特征及细观力学分析[J]. 煤炭学报,2016,41(3):611−617. WANG Wen, LI Huamin, YUAN Ruifu, et al. Micromechanics analysis and mechanical characteristics of water-saturated coal samples under coupled static-dynamic loads[J]. Journal of China Coal Society, 2016, 41(3): 611−617.
[12] 靳涛,连清旺. 饱和含水率对煤冲击层理效应影响研究[J]. 煤炭技术,2022,41(11):113−116. JIN Tao, LIAN Qingwang. Study on influence of saturated moisture content on coal impactbedding effect[J]. Coal Technology, 2022, 41(11): 113−116.
[13] 吴拥政,孙卓越,付玉凯. 三维动静加载下不同长径比煤样力学特性及能量耗散规律[J]. 岩石力学与工程学报,2022,41(5):877−888. WU Yongzheng, SUN Zhuoyue, FU Yukai. Mechanical properties and energy dissipation law of coal samples with different length diameter ratio under three-dimensional dynamic and static loading[J]. Chinese Journal of rock mechanics and engineering, 2022, 41(5): 877−888.
[14] ZHOU Yingxin, XIA Kaiwen, LI Xibing, et al. Suggested methods for determining the dynamic strength parameters and mode-I fracture toughness of rock materials[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 49(1): 105−112.
[15] 解北京,栾铮,陈冬新,等. 不同长径比煤样动力学特征及本构模型[J]. 矿业科学学报,2023,8(2):190−201. XIE Beijing, LUAN Zheng, CHEN Dongxin, et al. Dynamic characteristics and constitutive model of coal samples with different length diameter ratio[J]. Journal of Mining Science and Technology, 2023, 8(2): 190−201.
[16] 王海龙,李庆斌. 饱和混凝土静动力抗压强度变化的细观力学机理[J]. 水利学报,2006,37(8):958−962. WANG Hailong, LI Qingbin. Micro-mechanism of static and dynamic strengths for saturated concrete[J]. Journal of hydraulic engineering, 2006, 37(8): 958−962.
[17] 洪亮,李夕兵,马春德,等. 岩石动态强度及其应变率灵敏性的尺寸效应研究[J]. 岩石力学与工程学报,2008,27(3):526−533. HONG Liang, LI Xibing, MA Chunde, et al. Study on size effect of rock dynamic strength and strain rate sensitivity[J]. Chinese Journal of rock mechanics and engineering, 2008, 27(3): 526−533.
[18] ZHENG Dan, LI Qingbin. An explanation for rate effect of concrete strength based on fracture toughness including free water viscosity[J]. Engineering Fracture Mechanics, 2004, 71(16/17): 2319−2327.
[19] ROSSI P, MIER V J G M, BOULAY C, et al. The dynamic behavior of concrete: influence of free water[J]. Materials and Structures, 1992, 25(9): 509−514. doi: 10.1007/BF02472446
[20] ZHOU Zilong, CAI Xin, ZHAO Yuan, et al. Strength characteristics of dry and saturated rock at different strain rates[J]. Transactions of Nonferrous Metals Society of China, 2016, 26(7): 1919−1925. doi: 10.1016/S1003-6326(16)64314-5
[21] 金解放,余雄,钟依禄. 不同含水率红砂岩冲击过程中的能量耗散特性[J]. 有色金属科学与工程,2021,12(5):69−80. JIN Jiefang, YU Xiong, ZHONG Yilu. Energy dissipation characteristics of red sandstone with different water content during impact loading[J]. Nonferrous Metals Science and Engineering, 2021, 12(5): 69−80.
[22] BIAN Kang, LIU Jian, ZHANG Wei, et al. Mechanical behavior and damage constitutive model of rock subjected to water-weakening effect and uniaxial loading[J]. Rock Mechanics and Rock Engineering, 2019, 52(1): 97−106. doi: 10.1007/s00603-018-1580-4
[23] RAVICHANDRAN G, SUBHASH G. Critical appraisal of limiting strain rates for compression testing ceramics in a split Hopkinson pressure bar[J]. Journal of the American Ceramic Society, 1994, 77(1): 263−267. doi: 10.1111/j.1151-2916.1994.tb06987.x
[24] 郜欣,徐颖,李成杰,等. 不同应力比的循环荷载下砂岩变形损伤特性研究[J]. 中国安全生产科学技术,2021,17(11):60−64. GAO Xin, XU Ying, LI Chengjie, et al. Research on deformation and damage characteristics of sandstone under cyclic load with different stress ratios[J]. Journal of Safety Science and Technology, 2021, 17(11): 60−64.
[25] 张慧梅,陈世官,王磊,等. 扰动冲击下弱胶结红砂岩的能量耗散与分形特征[J]. 岩土工程学报,2020,39(9):1750−176. ZHANG Huimei, CHEN Shiguan, WANG Lei, et al. Energy dissipation and fractal characteristics of weakly cemented red sandstone under disturbance impact[J]. Chinese Journal of Geotechnical Engineering, 2020, 39(9): 1750−176.
[26] 王磊,袁秋鹏,谢广祥,等. 冲击载荷下煤样能量耗散与破碎分形的长径比效应[J]. 煤炭学报,2022,47(4):1534−1546. WANG Lei, YUAN Qiupeng, XIE Guangxiang, et al. Length-diameter ratio effect of energy dissipation and fractals of coal samples under impact loading[J]. Journal of China Coal Society, 2022, 47(4): 1534−1546.
[27] 解北京,于瑞星,陈冬新,等. 动载下石灰岩能耗指标影响因素研究[J]. 中国安全生产科学技术,2022,18(11):62−70. XIE Beijing, YU Ruixing, CHEN Dongxin, et al. Study on influencing factors of energy consumption index of limestone under dynamic load[J]. Journal of Safety Science and Technology, 2022, 18(11): 62−70.
[28] 宋常胜,王文,刘凯,等. 真三轴动静组合加载饱水煤样能量耗散特征[J]. 煤炭学报,2022,47(5):2011−2026. SONG Changsheng, WANG Wen, LIU Kai, et al. Energy dissipation characteristics of water saturated coal samples under true triaxial dynamic and static combined loading[J]. Journal of China Coal Society, 2022, 47(5): 2011−2026.
[29] 苏承东,孙玉宁,张振华,等. 饱水对煤层顶板砂岩单轴压缩破坏能量影响的分析[J]. 实验力学,2017,32(2):223−231. doi: 10.7520/1001-4888-16-118 SU Chengdong, SUN Yuning, ZHANG Zhenhua, et al. On the effect of water-saturated state on failure energy of sandstone from coal seam roof subjected to uniaxial compression[J]. Journal of Experimental Mechanics, 2017, 32(2): 223−231. doi: 10.7520/1001-4888-16-118
-
期刊类型引用(1)
1. 董志伟，杨世瑜，白帆，程晓强. 综采工作面瓦斯分源抽采技术研究与应用. 当代化工研究. 2025(03): 121-123 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 21
- HTML全文浏览量: 4
- PDF下载量: 1
- 被引次数: 1
