我国页岩气资源丰富，但是页岩气储层同时存在渗透性差、开采难度高等特点^[1-5]。为此，众多学者为有效提高页岩气储层的渗透性而进行研究并提出多种开采技术。其中，水力压裂技术为应用最为广泛的技术^[6-12]。为了优化水力压裂技术对页岩气储层渗透性的改造，有必要探究在对页岩气井进行水力压裂过程时影响其裂缝扩展的影响因素，特别是页岩气储层中含有层理构造时其水力裂缝扩展行为的影响因素。KAHRAMAN S等^[13]采用岩石脆塑性及断裂韧性等参数对储层的可压裂性进行评价；赵争光等^[14]采用地面微震技术证实储层的岩性是影响其水力裂缝扩展的重要因素；刘建中等^[15]采用物理模拟实验的方法发现水力裂缝在压裂后的延伸过程中会逐渐沿着垂直于最小水平主应力的方向扩展；门晓溪^[16]通过数值模拟发现储层中的层理角越大，其起裂压力越大；李晓等^[17]采用实验室试验的方法，得到层理倾角小于30°时页岩破裂所需破裂压力大，且破坏形态差异大的试验结果；HENG S等^[18]通过试验发现，在水力压裂过程中当水力裂缝和层理面相交时，穿透层理延伸的水力裂缝的缝高延伸速率显著低于沿层理扩展的水力裂缝；侯冰等^[19]采用实验室试验的方法，发现复杂的地质条件、脆性、发育的层理面和天然裂缝等会导致页岩在压裂后形成具有非平面、不对称和多分支行为的复杂水力裂缝网络。根据以上研究可知，鲜有针对施工参数（注液速率、液体黏度）对含层理页岩水力压裂过程中其水力裂缝扩展行为的影响规律研究。同时，考虑到理论分析无法对水力压裂过程中所产生的复杂裂缝进行合理解释，以及实验室研究无法进行基于工程尺度的水力压裂实验研究^[20-22]，采用离散元法对含层理页岩水力压裂过程中其水力裂缝的扩展行为进行数值模拟研究，以揭示液体黏度和注液速率对其影响规律。

1.   水力压裂控制方程

页岩气储层的水力压裂过程是一个涉及孔隙、裂缝、流体、应力等多相介质的复杂流固耦合问题，而块体离散元方法在模拟裂缝内的流固耦合行为上具有较高的优势。综合考虑本次数值模拟的研究目的可知，其控制方程主要涉及裂缝破坏的判定、节理内流体的流动及相关求解方程。

1.1   裂缝破坏判定

块体离散元方法通过块体间的节理面来模拟裂缝，节理面的破坏表示裂缝的开启。节理的本构模型为库伦滑移节理模型。在模型中均考虑了剪切和张拉失效，同时也考虑了节理的膨胀。在块体离散元方法中节理通过接触来描述，在弹性阶段，接触之间通过法向刚度与切向刚度来描述。节理的法向力学行为可表示为^[23]：

式中：$ \Delta {F}^{{\rm{n}}} $为法向力增量，N；$ {K}_{{\rm{n}}} $为法向刚度，N/m；$ \Delta {U}^{{\rm{n}}} $为法向位移增量，m；$ {A}_{{\rm{c}}} $为接触的面积，m²。

其剪切行为可以表示为^[23]：

式中：$ \Delta {F}_{i}^{{\rm{S}}} $为剪应力增量，MPa；$ {K}_{\mathrm{S}} $为切向刚度，N/m；$ \Delta {U}_{i}^{{\rm{S}}} $为切向位移增量，m。

节理（未发生滑移或开裂）的法向拉力的最大值$ {T}_{\mathrm{m}\mathrm{a}\mathrm{x}} $为：

式中：T为抗拉强度，MPa。

节理允许的最大剪切力$ {F}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{s}} $为：

式中：c为节理的黏聚力，MPa；$ \phi $为节理的摩擦角，（°）。

当节理上的力超过其抗拉或抗剪强度后，接触失效，同时节理的抗拉强度以及黏聚力变为 0。此时节理面上的最大拉力和最大剪切力可表示为：

这种失效后的强度的瞬间损失为节理面的“位移-弱化”行为。此时块体间新的接触力将会被更新（假设法向力压为正）。对于张拉失效，接触力的更新方式为：若$ {F}^{{\rm{n}}} < {T}_{{\rm{max}}} $，则法向力$ {F}^{{\rm{n}}}=0 $，剪切力$ {F}_{i}^{{\rm{S}}}=0 $；对于剪切失效，接触力的更新方式为：若$ {F}^{{\rm{n}}} > {F}_{{\rm{max}}}^{{\rm{s}}} $，则剪切力变为$ {F}_{i}^{{\rm{s}}}:={F}_{i}^{{\rm{s}}}\times {F}_{{\rm{max}}}^{{\rm{s}}} \div {F}^{{\rm{s}}} $，其中，剪切力$ {F}^{{\rm{s}}}={\left({F}_{i}^{{\rm{s}}}{F}_{i}^{{\rm{s}}}\right)}^{1/2} $。

剪切膨胀只发生在滑移模式。此时，剪切位移增量$ \Delta {U}^{{\rm{s}}} $可表示为：

剪切位移会引起法向的位移变化，其关系可由膨胀角$ \theta $来表征：

式中：$\Delta {U}^{{\rm{n}}}\left({\rm{dil}}\right)$为膨胀引起的法向位移。

此时法向力应该综合考虑膨胀的影响，法向力变为：

1.2   节理内流体流动

节理内的流体流动符合N-S方程。当2个面近似平行的非渗透面，且流体为不可压缩流体时，N-S方程可以简化为雷诺方程^[23]：

式中：u为平面上一点$ {x}_{i} $处的非渗透边界的距离，$ u=u\left({x}_{i}\right) $；h为水头高度，m；$ \rho $为流体密度，kg/m³；$ \mu $为流体黏度，Pa∙s；$ g $为重力加速度，m/s²。

根据式（11）可得到流体的流速V_i方程为：

式中：$ {u}^{2}/12\mathrm{为}\mathrm{单}\mathrm{裂}\mathrm{缝}\mathrm{渗}\mathrm{透} $；$k_{\rm{H}} $为水力传导率，${k}_{{\rm{H}}}={u}^{3}\rho g/12\mu$。

1.3   数值求解

在水力压裂中假设裂缝扩展行为主要由近尖端行为和流体整体体积平衡决定，裂缝扩展过程中主要有3种能量耗散方式：流体流动过程中的黏性能耗散、产生新裂缝（岩石断裂）所需的能量耗散以及流体滤失产生的能量耗散。对此，DONTSOV等^[23]给出了断裂韧度、流体黏度和滤失的圆盘状水力裂缝解模型。

以DONTSOV等提出的求解模型为基础并进行简化，在不考虑流体虑失的条件下，可得到黏性控制机制下裂缝开度$ {w}_{{\rm{m}}}\left(\rho ,t\right) $和裂缝半长$ {R}_{{\rm{m}}}\left(t\right) $的解析解分别为：

式中：$ {\mu }{{'}} $为与流体黏度相关参数，$ {\mu }{{'}}=12\mu $；$ {E}{{'}} $为与杨氏模量$ E $相关的参数，$ {E}{{'}}=E/\left(1-{v}^{2}\right) $，v为泊松比；$ {Q}_{0} $为注液速率，mL/s；t为注液时间，s。

而在断裂韧度控制机制下裂缝开度$ {w}_{{\rm{k}}}\left(\rho ,t\right) $和裂缝半长$ {R}_{{\rm{K}}}\left(t\right) $的解析解分别为：

式中：$ {K}{{'}} $为与岩石Ⅰ型断裂韧度$ {K}_{{\rm{IC}}} $相关的参数，$ {K}{{'}}=4\sqrt{2/\pi }{K}_{{\rm{IC}}} $。

2.   模型验证

为了验证块体离散元方法在模拟水力压裂中的可行性，基于上述2种控制机制的求解方式，分别选取一定的页岩属性参数来进行模拟，并将数值计算所得到的裂缝开度分布值与理论解进行对比。数值模拟参数见表1，数值模拟结果与理论解对比如图1。

表  1  数值模拟参数

Table  1.  List of numerical simulation parameters

控制机制	E' /Pa	µ' /（Pa·s）	K' /Pa	Q0 /（mL·s−1）	t /s
黏度	2.1117×1010	0.12	4.6117×106	1	1.5
韧性	2.1117×1010	1.2	4.6117×106	20	1.5

下载: 导出CSV 

| 显示表格

图  1  数值模拟结果与理论解对比

Figure  1.  Comparison between numerical simulation results and theoretical solutions

下载: 全尺寸图片 幻灯片

从图1可以看出，无论是黏度控制机制，还是韧性控制机制，采用块体离散元方法模拟所得到的裂缝开度分布的数值解与Donstov所建立的近似理论解匹配度极高。因此，可以认为，块体离散元法在页岩水力压裂中可以较好地模拟裂缝的扩展行为。

3.   水力裂缝扩展行为数值模拟

3.1   数值模型

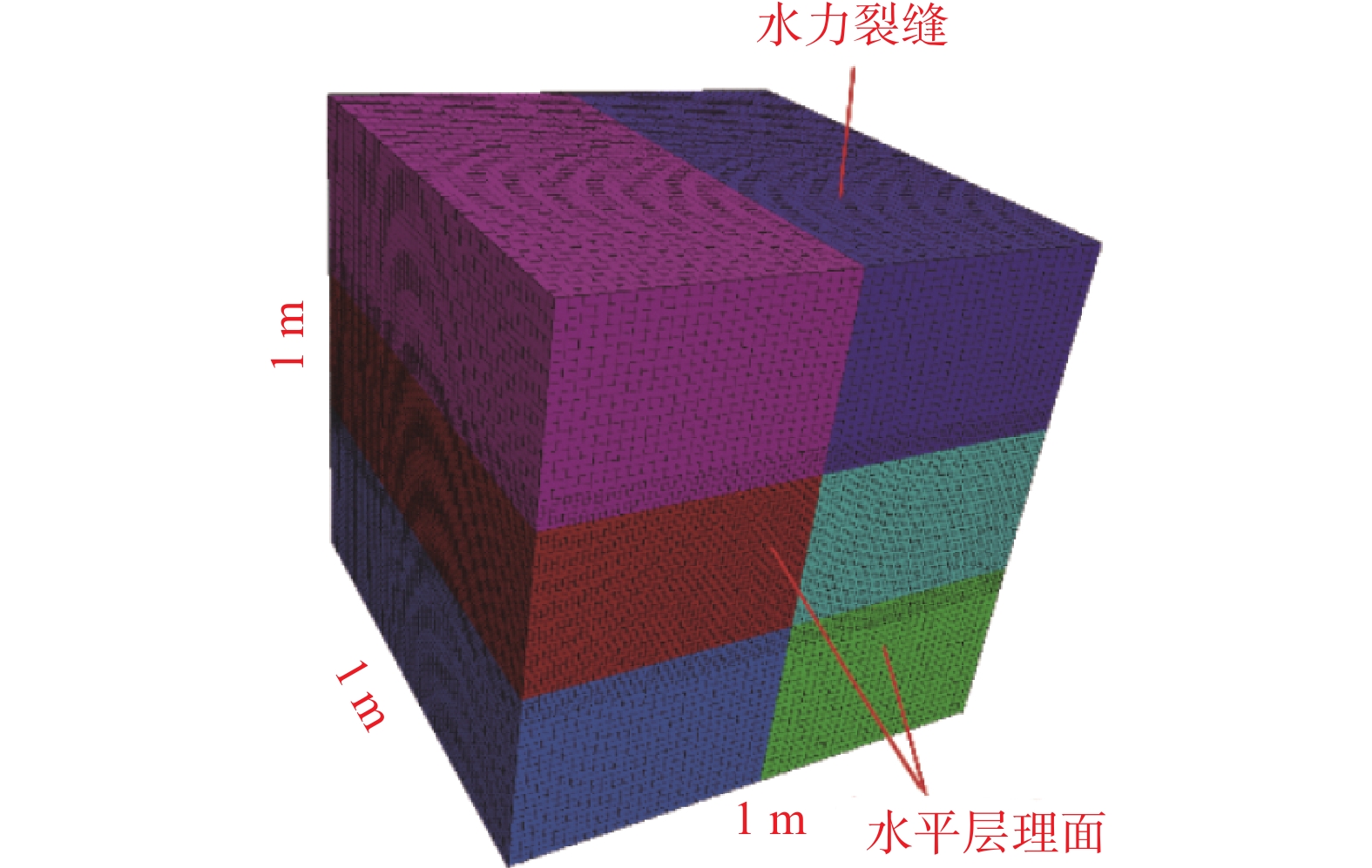
主要研究含层理页岩在水力压裂过程中，压裂液黏度及注液速率对水力裂缝扩展行为的影响，故建立数值模型，数值模型如图2。

图  2  数值模型

Figure  2.  Numerical model

下载: 全尺寸图片 幻灯片

模型尺寸为1.0 m×1.0 m×1.0 m，模型中包含1个垂向节理和2个水平节理。其中，垂向节理则作为预置的水力裂缝，用以模拟水力裂缝的竖向扩展；水平节理用来模拟2个水平层理面，2个层理面间距0.3 m。注入点设置在垂向节理面的中心位置，注入点距离2个水平层理面的距离相等。为了提高计算精度，在节理面附近进行网格加密。

此外，为了排除其他影响因素对模拟结果的影响，模拟中的地应力设置为均匀地应力（σ_x=σ_y=σ_z=20 MPa），节理参数设定为固定值（抗拉强度为10 MPa，黏聚力为5 MPa，摩擦角为20°），地层的流体压力设定为10 MPa。页岩的物理力学参数设定值分别为：密度2 600 kg/m³，弹性模量20 GPa，泊松比0.25。

3.2   数值模拟结果

3.2.1   压裂液黏度

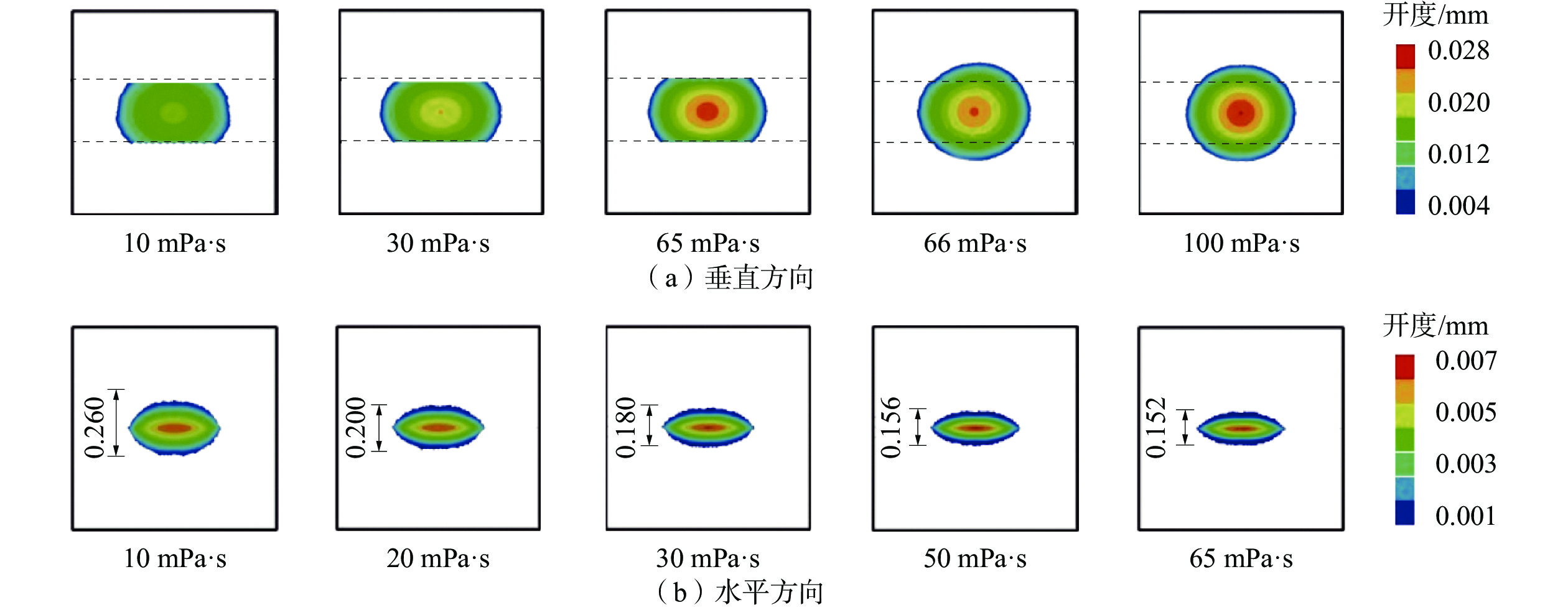
为探究压裂液黏度对水力裂缝扩展行为的影响规律，将注液速率设置为3 mL/s，分别模拟不同压裂液黏度（10～100 mPa·s，）下水力裂缝的扩展行为，不同压裂液黏度时水力裂缝在竖向的扩展行为（注液速率为3 mL/s）如图3。

图  3  不同压裂液黏度时水力裂缝在竖向的扩展行为（注液速率为3 mL/s）

Figure  3.  Vertical expansion behaviors of hydraulic fractures under different fracturing fluid viscosity conditions (liquid injection rate is 3 mL/s)

下载: 全尺寸图片 幻灯片

从图3可以看出：当压裂液黏度不超过 65 mPa·s时，水力裂缝未能穿过层理，且裂缝高度受到限制；当压裂液黏度不低于66 mPa·s时，水力裂缝穿过层理面并继续竖向扩展，且裂缝高度不受限制。这说明压裂液黏度会影响水力裂缝的穿层能力，低黏度有利于水力裂缝转向层理扩展，而高黏度则有利于水力裂缝穿过层理。进而分析可知，压裂液黏度对水力裂缝穿层行为的影响主要包含3点：①压裂液黏度会影响水力裂缝的分布形态，较低的压裂液黏度有利于水力裂缝转向，沿着水平层里面扩展，较高的压裂液黏度则有利于水力裂缝的穿层，沿着竖向延伸；②压裂液黏度会影响裂缝的开度，压裂液黏度较低时，裂缝开度较小且变化梯度较小，随着压裂液黏度的增加，裂缝开度也会随之增加，裂缝开度的分布梯度也会随之增大；③压裂液黏度会影响水力裂缝在水平层理面内的扩展，较低的压裂液黏度有助于水力裂缝沿水平层理面延伸，压裂液黏度越低，裂缝沿水平层理面的延伸距离越大。

3.2.2   注液速率

为探究注液速率对水力裂缝穿层能力的影响规律，在注液速率为3 mL/s的基础上，模拟1组注液速率为30 mL/s时不同压裂液黏度条件下水力裂缝的扩展行为，并采用对比不同注液速率下水力裂缝在竖向的扩展来对其进行分析，不同压裂液黏度时水力裂缝在竖向的扩展行为（注液速率为30 mL/s）如图4。

图  4  不同压裂液黏度时水力裂缝在竖向的扩展行为（注液速率为30 mL/s）

Figure  4.  Vertical expansion behaviors of hydraulic fractures under different fracturing fluid viscosity conditions (liquid injection rate is 30 mL/s)

下载: 全尺寸图片 幻灯片

从图4可以看出，当注液速率为30 mL/s时，水力裂缝的穿层能力同样表现出随其压裂液黏度的增加而增加的变化规律。此外，结合图3可知，注液速率为3 mL/s时影响水力裂缝穿过层理的压裂液黏度界限介于65～66 mPa·s之间，而注液速率为30 mL/s时影响水力裂缝穿过层理的压裂液黏度界限则介于8～9 mPa·s之间，这说明注液速率的增大，有效提高了水力裂缝的穿层能力，即大的注液速率更有利于水力裂缝穿过层理面。同时，当注液速率分别为3 mL/s和30 mL/s时，压裂液黏度为100 mPa·s时的裂缝开度分别为0.24 mm和0.37 mm，这说明随着注液速率的增大，裂缝开度也随之增加。

3.2.3   裂缝内压力分布

在模型中布置4个监测水力裂缝内压力的观测点，以便分析裂缝内的压力分布特征。观测点分布示意图如图5，其中，点1为注入点所在位置，点4位于竖向节理和横向节理的相交线上。

图  5  观测点分布示意图

Figure  5.  Distribution diagram of observation points

下载: 全尺寸图片 幻灯片

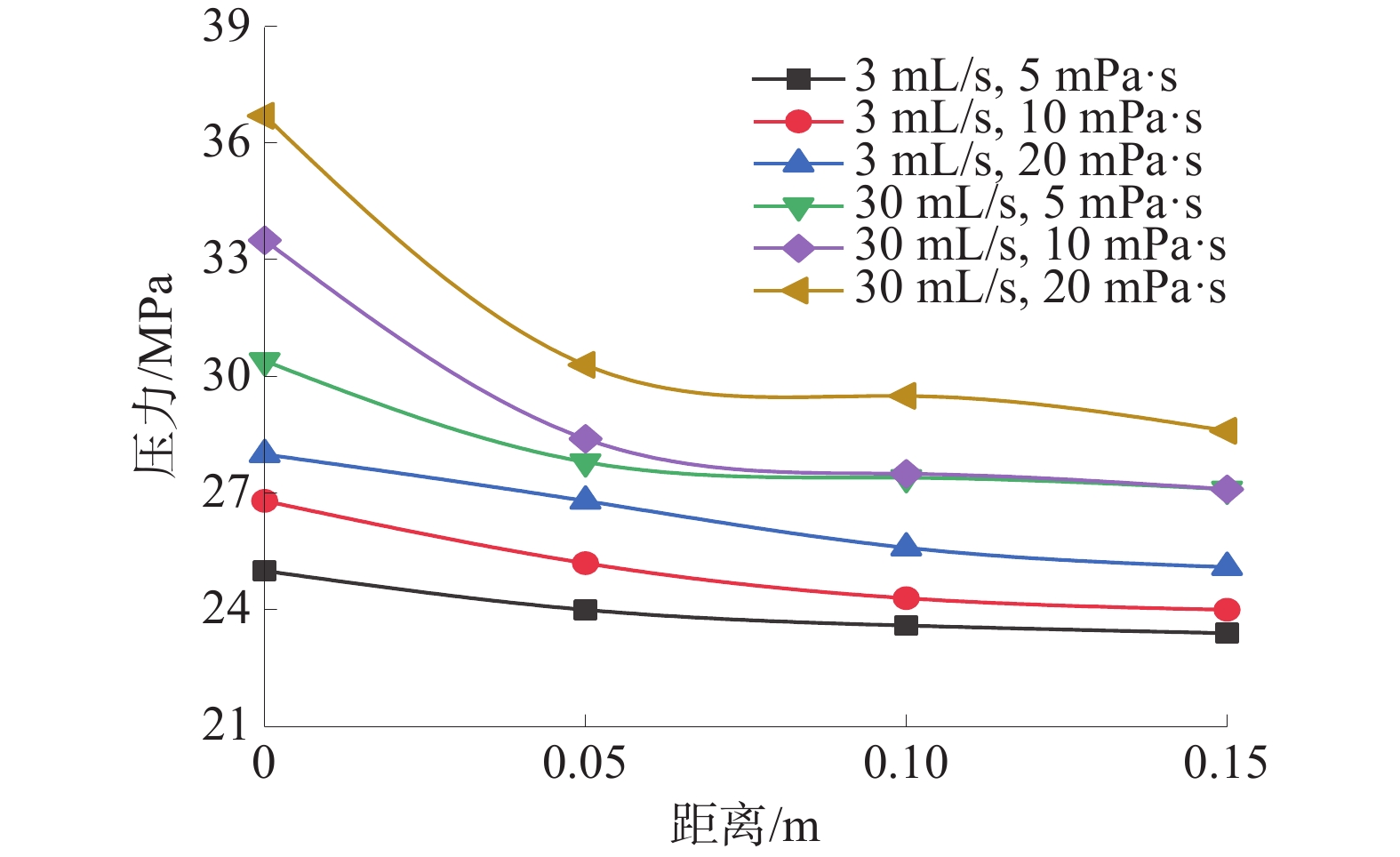
不同压裂液黏度及不同注液速率下，裂缝内的压力分布曲线如图6。

图  6  裂缝内的压力分布曲线

Figure  6.  Pressure distribution curves in fracture

下载: 全尺寸图片 幻灯片

从图6可以看出：裂缝内的压力从注入点向外逐渐降低，且在点 1 到点 2 之间（0.00～0.05 m）压力曲线的变化梯度最大，压力降低较快；而随着裂缝的不断扩展，向外侧压力衰减逐渐减慢；同时也可以看出，随着压裂液黏度和注液速率的上升，缝内压力逐渐上升，且分布越来越不均匀。

4.   结　语

1）基于块体离散元方法所建立的数值模型能够有效计算含节理页岩气储层水力压裂过程中的裂缝扩展问题。

2）较低的压裂液黏度和注液速率时，裂缝内压力较低且分布比较均匀，水力裂缝更倾向于转向层理扩展；较高的压裂液黏度和注液速率时，裂缝内压力较高且分布差异大，此时水力裂缝更趋向于穿过层理面竖向扩展。

3）裂缝内的压力从注入点向外逐渐降低，且随着裂缝的不断扩展，向外侧压力衰减逐渐减慢。