Study on micro-seismic detection in coalbed methane based on multiscale neural network
-
摘要:
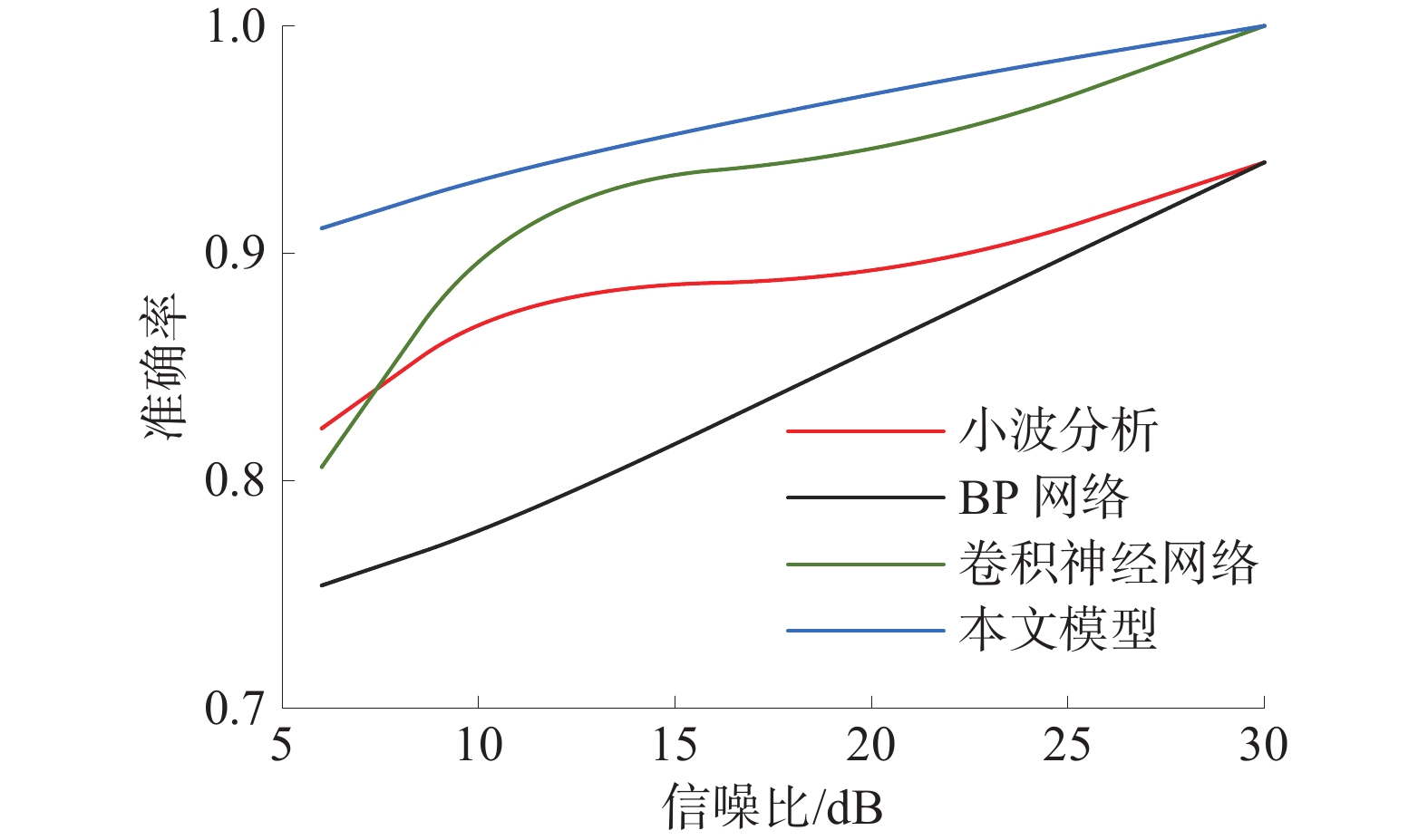
在煤层气勘探开发中,通过微地震监测技术掌握裂缝走向,调整采煤巷道位置、方位对安全生产具有重要意义。因此,提出一种基于多尺度卷积神经网络的微地震检测方法,较好地解决了在强干扰环境下的弱信号识别的问题。研究表明:在不同强度的噪声干扰下,本文方法的检测精确率和召回率均优于小波分析法、BP网络和卷积神经网络等方法,且具有较好的抗噪性。当信噪比大于6 dB时,模型检测召回率可达到90%以上,精确率可达到92.1%以上。通过黑龙江某地区实际煤层气微地震监测数据的验证,模型具有良好表现。
Abstract:In the exploration of coalbed methane, it is of great significance for safe production to master the direction of artificial fractures and adjust the position and orientation of coal mining roadway through micro-seismic monitoring technology. In this paper, a micro-seismic detection method based on a multi-scale convolutional neural network is proposed, which better solves the problem of weak signal recognition in a strong interference environment. The results show that the detection precision and recall rate of the proposed method is better than those of wavelet analysis, BP network, and convolutional neural network under different intensities of noise interference, and have good noise immunity. When the signal-to-noise ratio is greater than 6 dB, the model detection recall rate can reach more than 90%, the accuracy rate can reach more than 92.1%, and the model has good performance through the verification of the actual coal-bed methane micro-seismic monitoring data in a certain area of Heilongjiang Province.
-
Keywords:
- coalbed methane /
- micro-seismic detection /
- neural network /
- certainty factor /
- multiscale detection
-
CO气体无色无味,不易察觉,当超过一定浓度时存在爆炸危险,对井下工作人员的健康造成威胁,是煤矿开采过程中的安全隐患[1-2]。采用 CO 分析仪对煤矿 CO 进行及时的检测预报[3-5],对煤矿的安全生产具有重要的作用。针对 CO 分析仪的抗干扰能力进行研究,提高 CO 气体分析仪的可靠性及精度[6],为煤矿的安全生产提供保障。
目前,气体检测技术手段[7-9]主要包括催化燃烧式、热导式、光干涉式、电化学式等各类分析仪检测技术,以及色谱分析技术、光谱分析技术(傅里叶变换红外光谱FTIR、非分散红外光谱NDIR、可调谐半导体激光吸收光谱TDLAS、紫外差分吸收光谱UV-DOAS等)。国内外相关学者针对CO灾害气体选用不同的光谱分析技术,在提高气体检测精度和交叉干扰方面开展了大量的研究工作。TELEZHKO V M等[10]综述了气体分析仪用于测量工作区空气中有毒物质含量的优缺点;伍龙等[11]利用NDIR技术对煤矿井下CO进行定量探测,配合最小二乘法测量相对误差均小于5%,并提出对实验装置进行加热处理,可以降低反射池中的水汽含量,进而将水汽干扰降到最低;TAN等[12]利用NDIR技术对不同浓度范围的CO开展实验研究,提高了气体检测精度,检测误差降低到±0.05%;杜京义等[13]在温度和压力不稳定的情况下检测痕量CO浓度,针对测试出现的偏差,采用BP神经网络以及GA和PSO算法优化BP神经网络3种模型对CO浓度做出温压补偿,最后得出PSO优化BP神经网络效果最佳,测试相对误差缩小到1.55%;田富超[14]在检测煤矿井下气体浓度时建立了温度补偿后的矿用NDIR气体分析仪浓度计算模型,修正了传统意义上的朗伯比尔定律,降低了煤矿井下气体浓度受温度变化影响产生的误差,使得检测气体的精确度和可靠性取得了明显的改善;石锦涛[15]开展了高精度有毒有害气体的浓度检测技术研究,研发了可以同时测量多组分有毒有害气体浓度的检测样机,对CO气体进行低浓度检测,精度达到了0.1×10−6级别,单点光谱响应时间为0.001 368 s,非线性度为0.155 84;王前进等[16]提出的支持向量回归模型,在高浓度CH4环境下,微量CO气体绝对误差低于2×10−6;梁运涛等[17]、TIAN等[18]提出了不同温差下零点校正吸光度温度补偿方法,建立了温度补偿后矿用NDIR分析仪浓度定量分析模型,大大降低了因环境温度变化产生的系统误差;赵晓虎等[19]利用多路复用的锁相技术,设计了一套可以在线监测CO等煤自燃指标性气体的系统,并且在实验室分别测试得出系统对CO气体最低检出限可达0.12%。
以上学者选用了不同技术手段,在提高CO气体检测精度、灵敏度和降低测试误差方面取得了很大的成就,但是在复杂工况下分析精度欠缺,现有的温度补偿方法存在未考虑到现实环境温度变化复杂的问题,比如矿井生产环境会受季节更替影响,使得矿井温度一年四季会发生很大变化,进而导致分析仪产生较大偏差,不能准确分析待测气体组分和浓度。因此,搭建了试验平台,开展了分析仪精度分析测试,在变温条件下开展了不同体积分数CO气体分析仪温度补偿验证试验,进而建立了GA优化BP神经网络算法,有效降低了不同环境温度下气体浓度测试误差,提高了气体测试精度。
1. 实 验
1.1 实验平台
实验平台主要包括CO气体分析仪、标准气体、高精度配气仪以及数据采集平台。CO气体分析仪工作原理基于NDIR技术,量程为0~
1000 ×10−6,设置气体流经分析仪的流量为500 mL/min,避免气体流速太快带走热量,使分析仪内部温度发生明显变化。标准待测CO气体体积分数为1000 ×10−6,N2体积分数为99.999%,首先经过高精度配气仪,配比所需不同体积分数的目标气体;接着目标气体经过PU管进入CO分析仪;最后排出分析仪。数据采集平台将CO分析仪信号输出端与数据采集平台连接,可以实时传输分析仪测试气体的体积分数、分析仪温度以及测量次数。实验平台如图1所示,平台可以完成分析仪的标校和测试过程,为进一步分析气体精度和稳定性提供数据支撑。1.2 实验步骤
1)检查设备状态。分析仪开机预热30 min,确保吸收池温度参数基本保持不变。
2)测试前对分析仪标定。配比标准气体:采用高纯N2作为背景气体,使用高精度配气仪配比CO标准混合气体;仪器标零:通入的N2体积分数为99.999% ,标零之前,CO气体分析仪数据在0上下漂移;标零后,标定数据全部归零;仪器标量程:标量程时为确保待测气体精确性,最好选用满量程80%的标准气体,即选用的标准CO气体体积分数为800×10−6,在进气口先后通入N2、CO、N2,控制气体流速为500 mL/min,选择不同体积分数的CO气体通气5 min,待分析仪输出示数稳定后,点击标量程。
3)标校结束后,对分析仪精度和稳定性进行测试,采用类似于标量程的方法,通入配制好的待测气体,每组待测气体重复测试不低于360次,每次测试需要0.6 s完成,测试完毕后使用背景气体吹扫,排出分析仪内部残余的杂质气体。
1.3 分析方法
分析方法主要包括对比分析硬件温度补偿前后的误差,进而确定合适的补偿温度,通过改变环境温度,验证硬件温度补偿的可靠性,发现环境温度变化对硬件温度补偿后的传感器精度测试偏差较大,进而提出一种GA-BP神经网络补偿方法,并对比分析补偿前后的精度,发现神经网络补偿以后的传感器精度显著提高,最终实现井下不同环境温度条件下CO的精准测试,实验分析过程如图2所示。
根据式(1)~式(4)分别计算第$ i $次测试的绝对误差Wi、平均绝对误差值MAE、均方误差MSE和均方根误差RMSE。
$$ W_{i}=X_{i}-C $$ (1) $$ \mathrm{MAE}=\left|\sum_{i=1}^{i=a}X_i-nC\right|/n $$ (2) $$ {\mathrm{M S E}}=\sum_{i=1}^{i=n}\left(X_{{i}}-C\right)^{2} / n $$ (3) $$ {\mathrm{R M S E}}=\sqrt{\sum_{i=1}^{i=n}\left(X_{{i}}-C\right)^{2} / n} $$ (4) 式中:n为测试次数;Xi为第i次的测试体积分数值(i≤n,$ {i} \in N^{+} $),10−6;C为标准气体实际体积分数,10−6;Wi为第i次测试的绝对误差,10−6;MAE为平均绝对误差值,10−6;MSE为均方误差,(10−6)2;RMSE为均方根误差,10−6。
2. 实验结果
实验根据MT/T 757—2019《煤矿自然发火束管监测系统通用技术条件》[20] 进行,煤矿火灾气体监测仪器主要技术指标见表1。
表 1 煤矿火灾气体监测仪器主要技术指标Table 1. Standard technical indexes of fire gas monitoring system气体 体积分数
测量范围/10−6最大允许误差 CO 0~ 1000 0~100×10−6:±4×10−6 >100×10−6~500×10−6:±真值的5%
>500×10−6:±真值的6%2.1 加热温度
将未加热的CO分析仪分别放入高、低温试验箱,调节加热温度范围为25~55 ℃,测试温度每间隔5 ℃开展1组实验,选取标准CO气体体积分数为800×10−6,不同条件下的测试总时间为30 min,每组测试时间间隔5 min,求解多次测试结果的平均值得到测试结果,确保实验结果的准确性和可靠性,经过实验测试发现,分析仪精度随环境温度的变化而变化。分析仪加热温度对其测试精度的影响如图3所示。
通过多次测试发现:CO分析仪在加热温度为25~55 ℃范围内得到的CO体积分数测试值在700×10−6~950×10−6之间;加热温度为45 ℃时,得到的CO体积分数测试值最接近CO体积分数真实值800×10−6;其他加热温度下的体积分数测试绝对误差逐渐朝着45 ℃收敛。因此,CO分析仪的最佳工作温度为45 ℃。
2.2 温度补偿前后分析仪的精度
采用搭建的试验平台,对CO分析仪精度和稳定性开展实验测试,CO标准气体体积分数分别为10×10−6、100×10−6、500×10−6,每组分别进行360次重复性测试,确保实验数据的稳定性,分别得到了分析仪未加热补偿前和补偿后加热温度保持在45 ℃后理想的测试结果,测试结果如图4所示。
由图4可知:通过多次重复测试,温度补偿前,CO体积分数为10×10−6时的测量基本误差在(10~140)×10−6之间;CO体积分数为100×10−6时的测量基本误差在0~35×10−6之间;CO体积分数为500×10−6 时的测量基本误差在(100~140)×10−6之间,不满足MT/T 757—2019《煤矿自然发火束管监测系统通用技术条件》(表1)要求的最大允许误差。温度补偿后,CO体积分数为10×10−6 时的测量基本误差在0~3.5×10−6之间,CO体积分数为100×10−6时的测量基本误差在0~4.9×10−6之间,CO体积分数为500×10−6 时的测量基本误差在0~9×10−6之间,加热以后的CO分析仪对应体积分数下测试结果均优于表1中要求的最大允许误差,分析仪检测精度明显提高。
CO分析仪在稳定环境条件下,通过内部的恒温加热装置,使吸收池温度控制在45 ℃的恒定范围内,确保环境气体在流经吸收池的温度几乎不变,保证了温度补偿系数几乎不发生改变,进而可以达到气体检测精度高,检测下限低的效果。然而,煤矿环境条件往往更加复杂,需要进一步开展变温条件下分析仪温度补偿验证试验。
2.3 分析仪精度验证
实际应用过程中,添加恒温加热装置的分析仪在极度寒冷的环境下,往往不能满足前文提到的使分析仪内部温度恒定保持在45 ℃左右,这样就使得加温后稳定的温度补偿系数再次发生变化,导致分析仪测试精度再次发生偏移。基于此种现状,开展在高低温试验箱模拟环境温度,将稳定加热到45 ℃的CO分析仪放入高低温试验箱,调节环境温度为−15~45 ℃,每隔5 ℃开展1次系统测试,通过改变环境温度,测试分析仪的精度和稳定性。
选用真实CO体积分数分别为0、200×10−6、400×10−6、600×10−6、800×10−6、
1000 ×10−6开展实验测试,待测试数据稳定后,记录环境温度、CO分析仪温度以及CO分析仪体积分数测试结果。选取1 000组现场实验测试数据的平均值为最终测试CO平均体积分数,CO分析仪现场测试结果见表2。表 2 CO分析仪现场测试结果Table 2. Field test results of CO sensor环境
温度/℃分析仪
温度/℃测试CO体积分数/10−6 真实CO体积
分数为0真实CO体积分数为
200×10−6真实CO体积分数为
400×10−6真实CO体积分数为
600×10−6真实CO体积分数为
800×10−6真实CO体积
分数为1000 ×10−6−15 36.86 0.031 167.374 345.342 523.763 705.240 888.562 −10 41.67 0.100 188.799 380.130 564.312 734.173 926.701 −5 42.74 0.065 189.413 382.619 573.535 756.333 945.001 0 43.81 0.032 182.439 369.799 557.956 740.229 930.621 5 43.97 0.085 191.736 386.633 580.773 768.975 951.167 10 44.14 0.140 193.445 388.158 578.787 759.458 939.032 15 44.30 0.084 188.776 380.256 566.457 747.424 927.255 20 44.47 0.028 184.107 372.355 554.126 735.390 915.477 25 44.63 0.032 189.284 391.139 589.060 789.507 975.881 30 44.75 0.031 189.058 380.820 573.404 749.894 944.670 35 44.96 0.032 187.496 380.209 571.560 766.234 953.314 40 45.05 0.030 190.026 385.108 582.758 778.493 963.301 45 46.26 0.066 189.042 385.634 576.686 761.840 951.291 在CO分析仪内部添加独立的控温加热装置,可以最大限度地克服环境温度变化(比如环境温度−15 ℃,分析仪温度可达36.86 ℃),CO 温度拟合曲线如图5所示。随着环境温度T1的升高,分析仪温度T2上升趋势逐渐变平缓,采用线性公式拟合,拟合度高达
0.97702 。环境温度对分析仪测试精度的影响曲线如图6所示。从图6可以看出,环境温度对分析仪精度影响没有表现出非常明显的规律,在同一温度下,不同体积分数气体测试值变化规律一致,CO气体体积分数越大,环境温度对分析仪测试精度影响越大。
3. 数值模型
分析仪固定加热温度补偿技术,在一定程度上使得红外分析仪精度得到了显著提升,可以应用于环境温度相对稳定的工作场景中。然而,煤矿环境温度变化复杂,倘若使用硬件加热温度补偿的方式,可能导致分析仪出现信息误报,安全无小事,须引起高度重视。因此,还需要进一步开展分析仪精度优化研究。基于此,开展人工神经网络分析仪精度优选方法研究,建立一种GA-BP神经网络温度补偿模型,并选取小样本数据加以训练,以期达到煤矿气体检测数据优化、体积分数修正、信息融合等效果,最大程度降低分析仪精度受外界环境温度变化的影响。
3.1 GA-BP神经网络模型
人工神经网络(Artificial Neural Network,ANN)是建立在生物神经网络基础上的数据处理模型。模型将计算大量人工神经元的组合关系,根据外界约束条件调整自身的结构功能,通过改变神经元之间的权值对输入数据建立模型,利用模型约束输出数据,进而解决复杂非线性关系等实际问题。
误差反向传播(Error back propagation, BP)神经网络结构是一种多层传播的前向网络,学习方式为有监督学习网络。建立BP神经网络需要确定BP神经网络层数、每层神经元个数以及各层之间的权值系数,接着训练输入输出样本集,调整BP神经网络的权值和阈值,进而实现给定的输入、输出映射关系,给出正确的输出值。BP网络包含输入层、输出层和隐含层。设置输入层节点t(t=N)个,隐含层节点j(j≥5)个,输出层节点k(k=2)个,多层的网络设计,可以完成更复杂的求解任务。双隐含层的BP神经网络结构如图7所示。
遗传算法 (Genetic Algorithm,GA)[21]是通过借助模型仿真运算,将如何解决问题的具体过程转化为达尔文进化论中染色体遗传基因选择、交叉、变异的具体过程。在处理优化问题时,GA能够体现出更快更准确地优化效果[22],GA运算过程如图8所示。
单独的BP神经网络存在分类效果差、收敛速率慢、预测数据过拟合等问题。对此,提出GA-BP神经网络的多参量补偿方法,这种模型相比于其他分析方法的特点是:融合了神经网络的非线性拟合能力和遗传算法的全局搜索能力;遗传算法可以用于优化神经网络的权重和结构,以获得更好的性能。遗传算法是一种全局搜索算法,它可以帮助模型避免陷入局部最优解;BP神经网络以及其改进版本通常需要大量的训练数据,而GA-BP模型可以在有限的数据情况下表现出色;模型可以自适应地调整神经网络的结构和参数,以适应不同的温度补偿问题。GA-BP模型具有自适应性,减少了对人工参数调整的依赖。通过全局搜索和数据驱动方法,可以更好地泛化到未见的数据,从而提高了模型的实用性。GA-BP神经网络技术原理如图9所示。
将输入数据初始值经BP神经网络编码得出BP神经网络的权值、阈值长度,通过GA、BP神经网络进行多次迭代,获取最优权值、阈值,即不断更新BP神经网络的阈值、权值。通过GA-BP神经网络温度补偿优化模型对现场试验中得到的温度、体积分数测试值和体积分数真实值进行数据融合,计算全局最优结果。具体步骤如下:
1)数据清零初始化。
2)确定输入数据并进行预处理,导入待分析数据,将数据按特征指标进行划分,将温度、体积分数测试值作为输入数据,体积分数真实值作为输出数据,统计全部样本数目为N个,设定测试样本数目为w个,训练样本数目计算为(N-w)个。
3)划分BP神经网络的训练集与测试集。
4)得出初始BP神经网络权值阈值长度,获取输入层、输出层、隐含层节点个数。本文输入数据包含温度、体积分数测试值,因此确定输入层的节点数为2。输出数据包含体积分数真实值,确定输出层的节点数为1。在满足BP神经网络精度的前提下,确定隐含层节点个数的基本原则是尽量使用紧凑结构,即隐含层节点尽可能少。经过计算,测试得出最佳的隐含层节点数为12,相应的均方误差为
0.033156 。5)GA神经网络对初始值编码,构建最佳隐含层节点的BP神经网络。
6)初始值训练得到的绝对误差值作为GA神经网络适应度值。初始化种群规模设定70,迭代次数固定100次,交叉概率为0.8,变异概率设置为0.001[23],确定自变量个数以及上下限。调用GA函数,即依次调用轮盘赌选择、两点交叉和高斯变异函数,对样本适应度值进行求解,得出的适应度变化曲线如图10所示。
7)获取最优权值阈值。
8)训练GA-BP神经网络温度补偿模型。
9)测试GA-BP神经网络。
10)绘制CO仿真结果对比图。
3.2 小样本训练
针对CO气体分析仪在变温条件下得出的结果,利用传统的线性化修正方法是不可能的,为进一步提高分析仪在不同环境温度条件下测试精度,需要基于神经网络[24]对其精度进一步温度补偿,建立误差分析模型,使其可以满足在−15~45 ℃工作环境下的测试要求。提出一种基于GA-BP神经网络[25-26]的多参量补偿方法。将硬件温度补偿后的CO分析仪置于环境温度为25 ℃的条件下,对真实CO体积分数0、200×10−6、400×10−6、600×10−6、800×10−6、
1000 ×10−6开展测试,获取多组有效数据。利用MATLAB软件附带的随机选用函数挑选不同真实体积分数下若干组测试体积分数作为GA-BP神经网络温度补偿模型测试样本,剩余数据作为温度补偿模型的训练样本,开展CO分析仪温度补偿小样本训练。将训练小样本数据代入GA-BP优化算法运算过程中,经过仿真计算,当网络训练次数达到第
26745 次时,获得如所示最优的小样本仿真训练结果,即对应不同CO气体真实体积分数的BP预测值和GA-BP预测值,通过对比分析温度补偿模型的预测值和CO气体体积分数真实值之间的误差,确定神经网络训练的效果。CO训练样本见表3,CO训练效果如图11所示。表 3 CO训练样本Table 3. CO training samples样本
编号温度/
℃CO体积分数
测试平均值/10−6CO体积分数
真实值/10−6BP
预测值/10−6GA-BP
预测值/10−61 25 0.02943 0 21.4473 0.62143 2 25 171.40335 200 187.0858 201.94588 3 25 350.92902 400 391.9408 402.63002 4 25 528.84245 600 609.6235 596.44115 5 25 710.04265 800 804.1568 800.61630 6 25 880.59182 1000 1011.6112 996.81648 由图11可知:在训练的6个小样本中,以CO体积分数真实值为自变量,BP神经网络预测值、GA-BP神经网络预测值、实验测试值的拟合直线斜率分别为1.00、1.00、0.89,截距分别为2.9、1.93、−2.31,GA-BP神经网络预测值和BP神经网络预测值的拟合直线斜率均为1,而GA-BP神经网络预测值拟合直线截距更低,与全量程范围内的CO气体体积分数真实值贴合度更高,直观形象地说明GA-BP神经网络对于CO温度补偿的训练效果更佳。
3.3 优化算法误差分析
通过GA-BP神经网络初始权重和阈值优化,利用优化模型对验证试验中得到的温度、体积分数测试值和体积分数真实值进行数据融合,得到相应的仿真结果。CO样品组成见表4。
表 4 CO样品组成Table 4. CO samples composition样本编号 环境温度/℃ CO体积分数测试值/10−6 CO体积分数真实值/10−6 1 −15 0.0997 0 2 −10 0.0851 0 3 −5 0.2815 0 4 0 0.0319 0 $\vdots $ $\vdots $ $\vdots $ $\vdots $ 76 35 927.2545 1000 77 40 944.6701 1000 78 45 890.1425 1000 表4中样本编号1、4、7…75、78为测试集,其他点的测得体积分数为训练集。选取52组等距样本数据(占样本总数的2/3)进行训练建模,选取26组未参与训练的数据(占样本总数的1/3)进行模型性能检验。分别调用BP神经网络和GA-BP神经网络,参考气体体积分数的真实值,得到试验结果,CO优化对比如图12所示。
从2种方法的优化精度和稳定性来看,单独使用BP神经网络存在优化数据误差大、不连续点跳变、过拟合等问题。对于CO气体,单独使用BP神经网络补偿效果较差,而GA-BP对不同体积分数CO的补偿效果较好,这进一步说明GA-BP具有更广泛的适用性。神经网络算法误差分析如图13所示。
从图13补偿结果得出,初始的实验测试值得到的MAE值为
32.5127 ×10−6,标准BP神经网络修正CO的MAE值为27.3574 ×10−6,经GA-BP神经网络修正CO的MAE值为14.3751 ×10−6,对比分析补偿结果可以得出,2种神经网络对于实验测试值具有优化效果,GA-BP神经网络得到的MAE值较标准BP神经网络降低了12.9823 ×10−6,精度提高了47.5%。同时从MSE和RMSE的数据也可以得出GA-BP神经网络在灾害气体检测中的可行性,且能够提高分析仪检测精度,减少误报概率,通过此种方式可以实现煤矿不同环境温度条件下CO体积分数的精准化检测。4. 结 语
1)搭建了试验测试平台,涵盖温度补偿前、恒温加热测试、温度补偿后以及不同测试环境温度条件的红外气体分析仪实验平台;介绍了实验测试的方法,提出了数据误差分析的方法。
2)确定了CO分析仪最优的加热温度为45 ℃,并以3种不同体积分数的CO标准气体开展了分析仪硬件温度补偿前后对比分析。结果表明,在45 ℃条件下选用CO(体积分数10×10−6~500×10−6)标准气体进行了精度测试,计算CO气体绝对误差仅为0~9×10−6,误差优于煤矿火灾气体监测仪器主要技术指标规定的最大允许误差,测试结果稳定可靠。
3)对加热到45 ℃的CO分析仪开展模拟验证实验,发现CO分析仪测试精度受温度影响明显。基于此现象,建立了GA-BP神经网络模型,利用优化模型对验证试验中得到的温度、体积分数测试值和体积分数真实值进行数据融合,并且计算得出GA-BP神经网络得到的MAE值较标准BP神经网络降低了
12.9823 ×10−6,精度提高了47.5%,进而确保了CO分析仪的稳定性和精度,为火灾气体实时在线监测提供了一定的技术支撑。 -
表 1 模型检测结果
Table 1 Detection results of model
噪声大小/dB TP FN TN FP ACC/% 无噪声 400 0 400 0 100 21 390 10 389 11 97.38 11 373 27 377 23 93.75 6 360 40 369 31 91.13 注:TP为真实值为1,预测值为1;FN为真实值为1,预测值为0;TN为真实值为0,预测值为0;FP为真实值为0,预测值为1。 表 2 不同方法在不同噪声强度下的精确率
Table 2 Accuracy rates of different methods under different noise intensities
噪声大小/dB 无噪声 21 11 6 小波分析法 0.942 1.000 0.994 0.862 BP网络 0.942 0.877 0.794 0.751 CNN模型 1.000 0.954 0.926 0.804 本文方法 1.000 0.973 0.942 0.921 表 3 不同方法在不同噪声强度下的召回率
Table 3 Recall rates of different methods under different noise intensities
噪声大小/dB 无噪声 21 11 6 小波分析法 0.938 0.778 0.775 0.768 BP网络 0.938 0.853 0.763 0.76 CNN模型 1.000 0.933 0.932 0.81 本文方法 1.000 0.975 0.933 0.90 -
[1] 谭辰阳,张占松,周雪晴,等. 基于随机森林算法的煤层气产能模式识别模型[J]. 煤矿安全,2022,53(2):170−178. TAN Chenyang, ZHANG Zhansong, ZHOU Xueqing, et al. Pattern recognition model of coalbed methane productivity based in random forest algorithm[J]. Safety in Coal Mines, 2022, 53(2): 170−178.
[2] 金之钧,张金川,唐玄. 非常规天然气成藏体系[J]. 天然气工业,2021,41(8):58−68. JIN Zhijun, ZHANG Jinchuan, TANG Xuan. Unconventional natural gas accumulation system[J]. Natural Gas Industry, 2021, 41(8): 58−68.
[3] 侯玮,霍海鹰,田端信,等. 基于微震监测的煤矿防治水预测方法[J]. 煤矿安全,2013,44(9):143−145. HOU Wei, HUO Haiying, TIAN Duanxin, et al. The prediction method of mine water prevention and control based on microseismic monitoring[J]. Safety in Coal Mines, 2013, 44(9): 143−145.
[4] MAXWELL S C, RUTLEDGE J, JONES R, et al. Petroleum reservoir characterization using downhole microseismic monitoring[J]. Geophysics, 2010, 75(5): 129−137.
[5] 张岩,李新月,王斌,等. 基于联合深度学习的地震数据随机噪声压制[J]. 石油地球物理勘探,2021,56(1):9−25. ZHANG Yan, LI Xinyue, WANG Bin, et al. Randomnoise suppression of seismic data based on joint deep learning[J]. Oil Geophysical Prospecting, 2021, 56(1): 9−25.
[6] 田峰. 地面微地震压裂监测技术在煤层气开发中的应用[J]. 中国煤炭地质,2018,30(8):75−78. doi: 10.3969/j.issn.1674-1803.2018.08.14 TIAN Feng. Application of surface microseismic fracturing monitoring technology in CBM exploitation[J]. Coal Geology of China, 2018, 30(8): 75−78. doi: 10.3969/j.issn.1674-1803.2018.08.14
[7] 王秀荣,赵镨,程彦,等. 淮南地区煤层气压裂地面微震监测技术研究[J]. 中国煤炭地质,2021,33(10):140−147. doi: 10.3969/j.issn.1674-1803.2021.10.27 WANG Xiurong, ZHAO Pu, CHENG Yan, et al. Study on CBM fracturing surface microseismic monitoring technology in Huainan Area[J]. Coal Geology of China, 2021, 33(10): 140−147. doi: 10.3969/j.issn.1674-1803.2021.10.27
[8] 宋维琪,吕世超. 基于小波分解与Akaike信息准则的微地震初至拾取方法[J]. 石油物探,2011,50(1):14−21. doi: 10.3969/j.issn.1000-1441.2011.01.002 SONG Weiqi, LV Shichao. Automatic detection method of microseismic event based on wavelet decomposition and Akaike information criteria[J]. Geophysical Prospecting for Petroleum, 2011, 50(1): 14−21. doi: 10.3969/j.issn.1000-1441.2011.01.002
[9] 刘栋,李夕兵,刘志祥,等. 基于STSNN聚类算法的用沙坝矿微震事件活动特征研究[J]. 中国安全生产科学技术,2017,13(2):74−78. LIU Dong, LI Xibin, LIU Zhixiang, et al. Study on activity characteristics of microseismic events in Yongshaba Mine based on STSNN clustering algorithm[J]. Journal of Safety Science and Technology, 2017, 13(2): 74−78.
[10] 王维波,徐西龙,盛立,等. 卷积神经网络微地震事件检测[J]. 石油地球物理勘探,2020,55(5):939−949. WANG Weibo, XU Xilong, SHENG li, et al. Microseismic event detection based on convolution neural network[J]. Oil Geophysical Prospecting, 2020, 55(5): 939−949.
[11] 翟尚,喻志超,谭玉阳,等. 基于波形聚类分析的微地震监测事件类型判别及应用[J]. 北京大学学报(自然科学版),2020,56(3):406−416. ZHAI Shang, YU Zhichao, TAN Yuyang, et al. Microseismic monitoring events classification based on waveform clustering analysis and application[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2020, 56(3): 406−416.
[12] COVA David,刘洋,丁成震,等. 人工智能和视速度约束的地震波初至拾取方法[J]. 石油地球物理勘探,2021,56(3):419−435. COVA David, LIU Yang, DING Chengzhen, et al. First break picking method based on artificial intelligence and apparent velocity constraint[J]. Oil Geophysical Prospecting, 2021, 56(3): 419−435.
[13] 蔡振宇,盖增喜. 人工智能在拾取地震P波初至中的应用-以汶川地震余震序列为例[J]. 北京大学学报(自然科学版),2019,55(3):451−460. CAI Zhenyu, GE Zengxi. Using artificial intelligence to pick P-wave first arrival of the microseisms: taking the aftershock sequence of Wenchuan earthquake as an example[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2019, 55(3): 451−460.
[14] TU M. Gesture Detection and Recognition Based on Pyramid Frequency Feature Fusion Module and Multiscale Attention in Human Computer Interaction[J]. Mathematical Problems in Engineering, 2021, 2021(7): 1−10.
[15] LIU W, ANGUELOV D, ERHAN D, et al. SSD: Single shot multi box detector[C]// Computer Vision-ECCV2016. Springer, Cham: Springer International Publishing, 2016: 21-37.
[16] CAI Z, FAN Q, FERIS R S, et al. A unified multi-scale deep convolutional neural network for fast object detection[C]// Computer Vision-ECCV2016. Springer, Cham: Springer International Publishing, 2016: 354-370.
[17] ARTUN Emre,KULGA Burak. 基于模糊推理的致密砂岩气储集层重复压裂井选择方法[J]. 石油勘探与开发,2020,47(2):383−389. doi: 10.11698/PED.2020.02.17 ARTUN Emre, KULGA Burak. Selection of candidate wells for re-fracturing in tight gas sand reservoirs using fuzzy inference[J]. Petroleum Exploration and Development, 2020, 47(2): 383−389. doi: 10.11698/PED.2020.02.17




 下载:
下载: