瓦斯是导致煤矿安全事故发生的主要危险因素之一，瓦斯涌出量的精准预测是预防煤矿瓦斯灾害事故发生的重要前提^[1]。瓦斯涌出量预测方面，传统的矿山统计法、分源预测法、瓦斯地质统计法和类比法等预测周期相对较短，且未考虑瓦斯涌出的动态非线性特征^[2-3]。

近年来，为解决这一问题，基于机器学习算法的瓦斯涌出量动态预测得到快速发展，主要分为考虑影响因素和时间序列2类预测方法^[4-7]。由瓦斯涌出量预测影响因素建立的多因素指标预测方法，因各煤矿的基本情况千差万别，导致影响瓦斯涌出量预测的指标权重也大相径庭，且对不易量化的影响因素难以确定，加之瓦斯涌出量预测影响因素众多，使得构建的预测模型与实际情况仍有一定差距。因此，诸多学者对瓦斯涌出量时间序列预测展开了研究和分析。潘结南等^[8]提出了R/S时间序列分析方法，并应用于矿井瓦斯涌出量预测；黄文标等^[9]针对存在于传统线性预测方法的问题，建立了基于最大Lyapunov指数的瓦斯涌出量时间序列预测模型；李润求等^[10]建立了采煤工作面瓦斯涌出量时间序列预测的EMD-Elman方法，有效显示采煤工作面瓦斯涌出量的波动性、周期性和趋势性等非线性特征，降低了瓦斯涌出量非平稳性对预测结果的影响，具有较高的预测精度；施式亮等^[11]建立了预测瓦斯涌出量的EMD-PSO-SVM方法，其对非平稳时间序列预测有较强的适用性；撒占友等^[12]提出一种基于经验模态分解（EMD）和ARMA时间序列的综合分析方法，建立EMD-ARMA预测模型，对矿井瓦斯涌出量及其变化趋势进行了预测；王永文^[13]构建了基于HHT-CS-ELM的瓦斯涌出量动态预测模型，证明了该模型具有较高的预测精度和泛化能力；林海飞等^[14]构建了STL-EEMD-GA-SVR预测模型（SEGS），通过与其他模型的精度评价指标进行对比分析，SEGS模型最优，可以准确预测采煤工作面的瓦斯涌出量。

上述预测模型均考虑了瓦斯涌出量非平稳、非线性的数据特征对预测精度的影响。为了进一步提高瓦斯涌出量预测精度，利用VMD与CEEMDAN处理非线性、非平稳序列的优点，结合BiLSTM对时间序列有着良好的学习、记忆和预测性能，并针对BiLSTM模型中的超参数难以确定且耗时较长的问题，将贝叶斯优化算法（BO）引入BiLSTM中确定模型超参数，以充分发挥模型的最大性能，从而建立基于二次分解和贝叶斯优化BiLSTM的采煤工作面瓦斯涌出量预测模型（VMD-CEEMDAN-BO-BiLSTM）；以陕西彬长某矿采煤工作面绝对瓦斯涌出量监测数据为例进行建模和预测分析，并选取5组机器学习算法作为对照模型，通过各模型预测结果的对比分析来验证本文所建模型的稳定性、可靠性和优越性。

1.   模型原理

1.1   二次分解

1.1.1   变分模态分解

变分模态分解（VMD）^[15]是一种自适应分解方法，可以有效降低瓦斯涌出量时序数据的非平稳性。具体步骤如下：

1）根据预先设定的分解个数k，对原始信号f（t）进行分解，得到的各分量具有中心频率的有限带宽，用希尔伯特变换解析信号后，将信号平移到基带并混合中心频率估计信号带宽，使得各分量的估计带宽最小，且各分量之和与原始信号相同。变分模型函数为：

式中：$ \left\{ {{\mu _k}} \right\} $、$ \left\{ {{\omega _k}} \right\} $分别为分解后第k个本征模态分量和中心频率的集合；$ \delta \left( t \right) $为脉冲函数；$ \phi $为虚数单位；$ {\mu _k}\left( t \right) $为模态函数；k为分解得到的模态数。

2）引入拉格朗日乘法算子λ和二次惩罚因子α，将式（1）转化为增广拉格朗日函数L（$ \left\{ {{\mu _k}} \right\} $,$ \left\{ {{\omega _k}} \right\} $,λ），其公式为：

3）本征模态分量和中心频率的迭代更新公式如下：

式中：$\hat f\left( \omega \right)$、${\hat \mu _k}\left( \omega \right)$、$\hat \lambda \left( \omega \right)$分别为$f\left( t \right)$、${\mu _k}\left( t \right)$、$\lambda \left( t \right)$的傅里叶变换。

通过以上步骤，完成原始信号的变分模态分解，其中模态分量个数$ k $对模型的预测精度有较大影响，若$ k $值过大会导致数据被过度分解，造成模态混叠问题，而$ k $值过小则会导致VMD欠分解，使子序列无法完全表征原始数据的特征。

1.1.2   自适应噪声完备经验模态分解

自适应噪声完备经验模态分解（CEEMDAN）是一种在EMD和EEMD方法的基础上改进的信号分解方法。经验模态分解（EMD）方法在信号分解过程中会出现模态混叠现象^[16]。WU等^[17]基于EMD提出了集合经验模态分解（EEMD）方法，但分解后残留的白噪声导致分解具有较差的完整性。而CEEMDAN方法通过多次在每一个分解阶段中加入自适应的高斯白噪声，有效解决了EMD和EEMD方法模态混叠问题以及重构序列中存在残留噪声的现象，具有较好的分解完整性，能对原始信号进行精确重构。该算法的实现过程如下：

1）将待分解的信号$ x\left( t \right) $添加$ N $次均值为0的高斯白噪声序列，构造共$ N $次实验的待分解序列$ {x_i}\left( t \right)\left( {i = 1,2, \cdot \cdot \cdot ,N} \right) $。

式中：$ \varepsilon $为高斯白噪声权值系数；$ {\chi _i}\left( t \right) $为第$ i $次添加的白噪声序列。

2）对$ {x_i}\left( t \right) $采用EMD方法进行信号分解，得到第1个IMF模态分量以及第1个唯一残余分量$ {r_1}\left( t \right) $。

3）将分解得到的第$ j\left( {j = 2,3, \cdot \cdot \cdot ,N} \right) $阶段残余分量添加噪声继续应用EMD进行分解。

4）重复执行步骤3），直至满足终止条件。终止准则为余量信号极值点数至多不超过2个。最终，原始信号序列被分解为$ N $个模态分量和残差项$ R\left( t \right) $。

1.2   双向长短期记忆网络（BiLSTM）

长短期记忆网络（LSTM）考虑了输入和输出之间的时间关系，在瓦斯涌出量预测中得到了一定应用^[18]，LSTM单元分别由输入门、遗忘门、和输出门组成，具体为：

式中：$ {i_t} $、$ {f_t} $、$ {o_t} $分别为输入门限值、遗忘门限值和输出门限值；$ \sigma $为sigmoid激活函数；$ {{\boldsymbol{W}}_i} $、$ {{\boldsymbol{W}}_f} $、$ {{\boldsymbol{W}}_O} $分别为输入门、遗忘门、输出门的权重矩阵；$ {x_t} $、$ {h_t} $分别为输入和输出序列；$ {b_i} $、$ {b_f} $、$ {b_o} $为常数。

LSTM单元在时间t内的中间状态$ {C_t} $由$ {\tilde C_t} $和$ {C_{t - 1}} $确定，最终得到该单元在时段t的预测值$ {h_t} $，具体由下式给出：

式中：tanh为双曲正切激活函数； $ {{\boldsymbol{W}}_c} $为中间状态的权重矩阵；$ {b_{\mathrm{c}}} $为常数；$ \otimes $为矩阵乘积运算符。

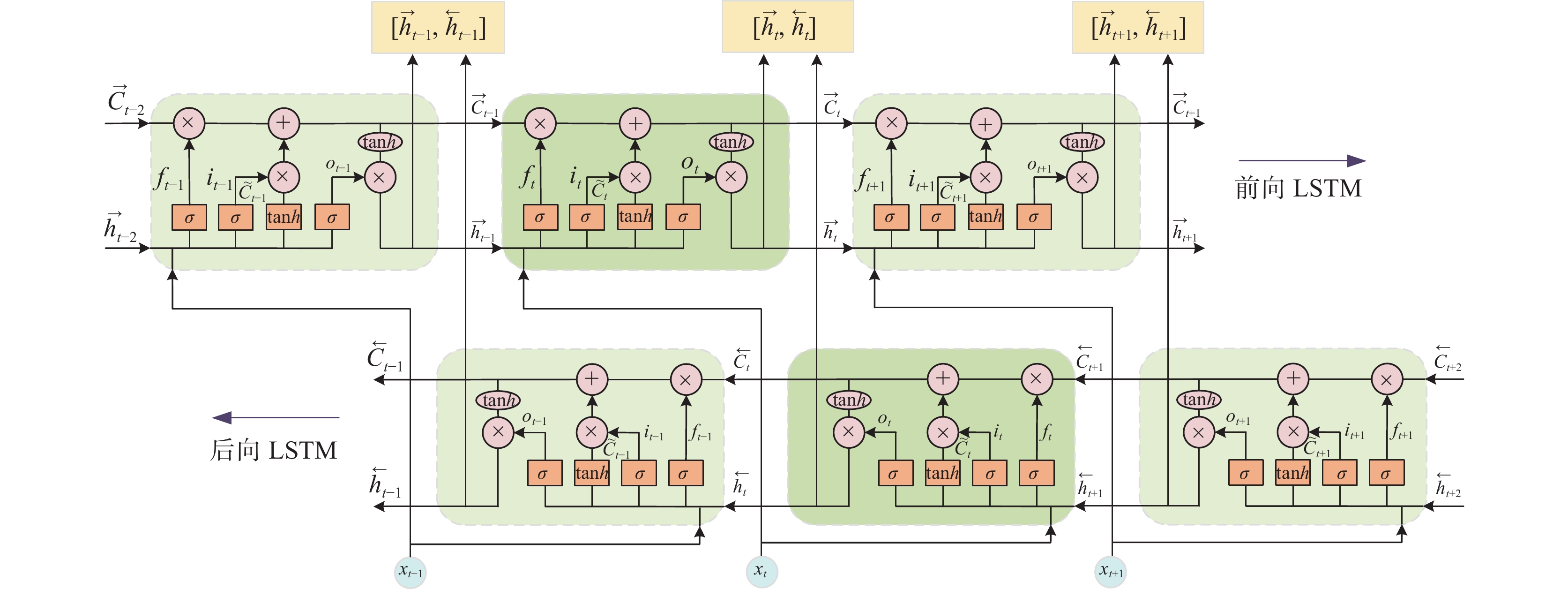
双向长短期记忆网络（BiLSTM）是由前向LSTM和后向LSTM共同组成的，前向LSTM获取输入时间序列的过去信息，后向LSTM获取输入时间序列的未来信息，可对时序数据的正向和逆向信息进行同时处理，因此能够更加深入的挖掘瓦斯涌出量数据中所包含的时序信息^[19]，因此选取其作为本文时序预测模型的核心算法。BiLSTM神经网络结构如图1所示。

图  1  BiLSTM神经网络结构

Figure  1.  Structure of BiLSTM neural network

下载: 全尺寸图片 幻灯片

BiLSTM模型输出为形如$ \left[ {{{\vec h}_t},{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{h} }_t}} \right] $的数组，为得到瓦斯涌出量最终预测值$ {y_t} $，需通过式(17)中的函数y_t进行合成。

式中：$ \varphi $为合成函数，可为sigmoid、relu、tanh等函数或线性加权操作。

1.3   贝叶斯优化算法（BO）

贝叶斯优化算法因具有收敛速度快、性能好、可扩展性强等优点被广泛应用于超参数的自动寻优。其基本原理为贝叶斯定理估计目标函数的后验分布，然后根据对目标函数过去的评估结果建立代理模型，找到下1个最小目标值的超参数组合。贝叶斯定理估计目标函数如式(18)：

式中：$ p\left( {l\left| D \right.} \right) $为$ l $的后验概率；$ l $为目标函数；$ D $为已观测参数和观测值的集合，$ D = \left\{ \left( {{x_1},{z_1}} \right), \left( {{x_2},{z_2}} \right), \cdot \cdot \cdot ,\left( {{x_t},{z_t}} \right) \right\} $；$ {x_t} $为观测参数；z_t为观测值；$ p\left( l \right) $为$ l $的先验概率；$ P\left( {\left. D \right|l} \right) $为$ l $的似然分布；$ p\left( D \right) $为$ l $的边际似然分布。

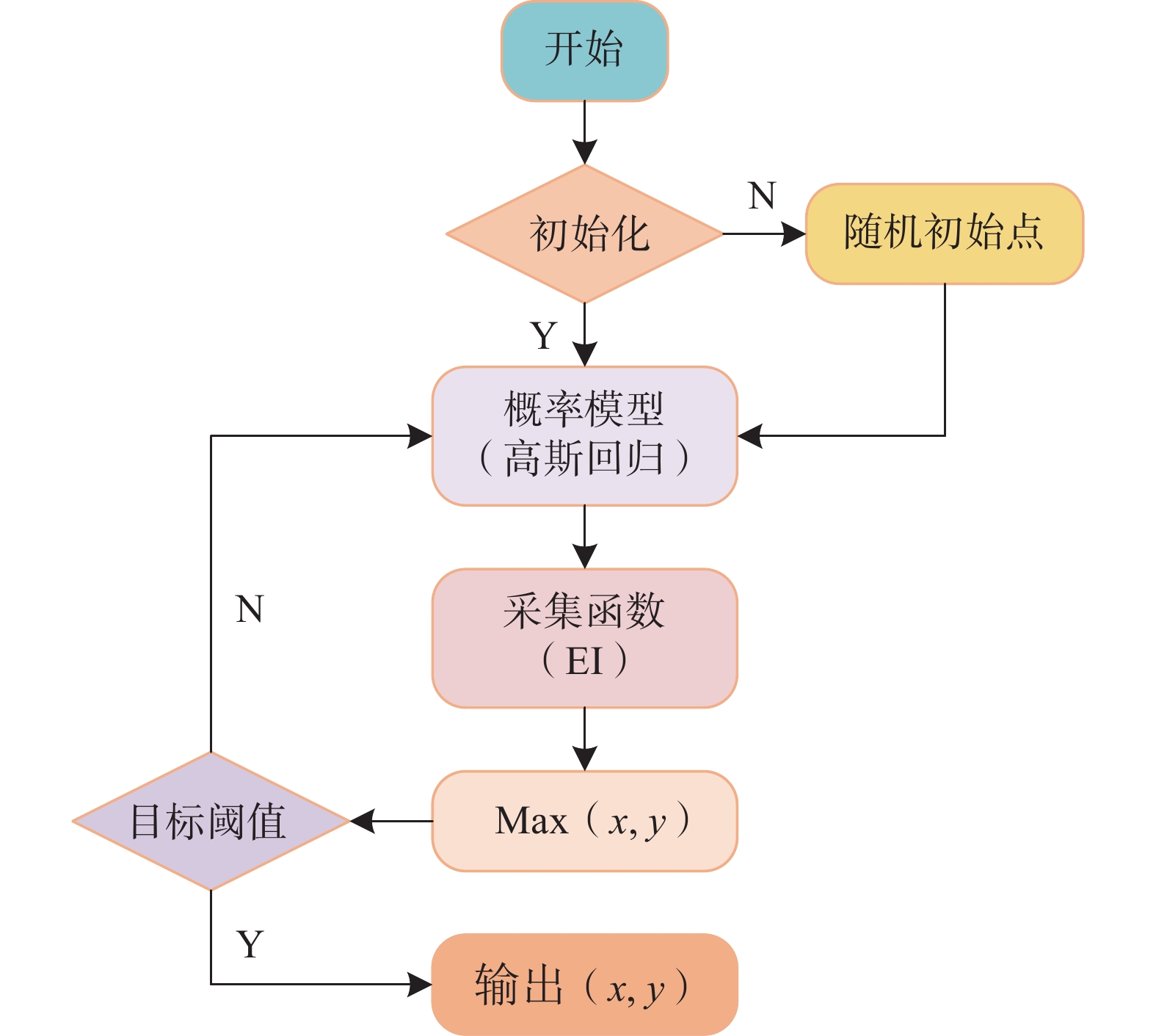
贝叶斯优化算法有2个核心部分：概率模型和采集函数。文中概率模型采用高斯过程（GP）回归，采集函数选择预期改进（EI）函数。贝叶斯优化过程如图2所示。

图  2  贝叶斯优化过程

Figure  2.  Process of Bayesian optimization

下载: 全尺寸图片 幻灯片

高斯过程（GP）是指随机变量的1个集合，是贝叶斯优化算法中应用最普遍的概率模型^[20]。高斯过程的核心是由1个均值函数$ \upsilon \left( x \right) $和1个半正定协方差函数$ g\left( {x,x} \right) $共同构成的，其形式如下：

式中：$ \upsilon \left( x \right) = E\left( {l\left( x \right)} \right) $；$ E\left( {l\left( x \right)} \right) $为$ l\left( x \right) $的数学期望，一般均值函数$ \upsilon \left( x \right) $为0；$ l\left( x \right) $为平均绝对误差；$ g\left( {x,x} \right) $为$ x $的协方差函数。

假设从模型获取的历史信息为$ {D_{1:t}} = \left\{ {{x_{1:t}},{l_{1:t}}} \right\} $，其中$ {l_t} = l\left( {{x_t}} \right) $，搜寻的下1个值为$ {x_{t + 1}} $，协方差矩阵$ {\boldsymbol{G}} $如式(20)：

根据高斯过程的性质，$ {l_t} $和$ {l_{t + 1}} $都服从联合高斯分布，假设其均值为0，则联合高斯分布如式(21)：

通过求其边缘密度函数，可以得到$ {l_{t + 1}} $的后验概率：

式中：$ {\upsilon _t}\left( {{x_{t + 1}}} \right) $为数学期望；$ \eta _t^2\left( {{x_{t + 1}}} \right) $为方差。

采集函数（EI）的作用是根据更新的后验概率分布寻找最大改善期望的下1个样本点$ {x_{t + 1}} $，当标准差$ \eta \left( x \right) = 0 $时，采集函数$ {\mathrm{EI}}\left( x \right) = 0 $；当标准差$ \eta \left( x \right) > 0 $时，其采集函数计算公式表示为：

式中：$ \xi $为权衡标量，$ \xi $$ > $0；$ \varPhi \left( \cdot \right) $为标准正态分布的概率密度函数；$ \phi \left( \cdot \right) $为标准正态分布的分布函数。

其中，$ Z $可表示为：

1.4   误差评估

采用均方根误差（RMSE）、平均绝对误差（MAE）和平均绝对百分比误差（MAPE）对模型预测精度进行评估，各指标计算公式为：

式中：$ m $为测试集样本数；$ {\hat y_{{\mathrm{test}},i}} $为测试集预测瓦斯涌出量，m³/min；$ {y_{{\mathrm{test}},i}} $为测试集实测瓦斯涌出量，m³/min。

2.   瓦斯涌出量预测模型

2.1   VMD-CEEMDAN-BO-BiLSTM模型

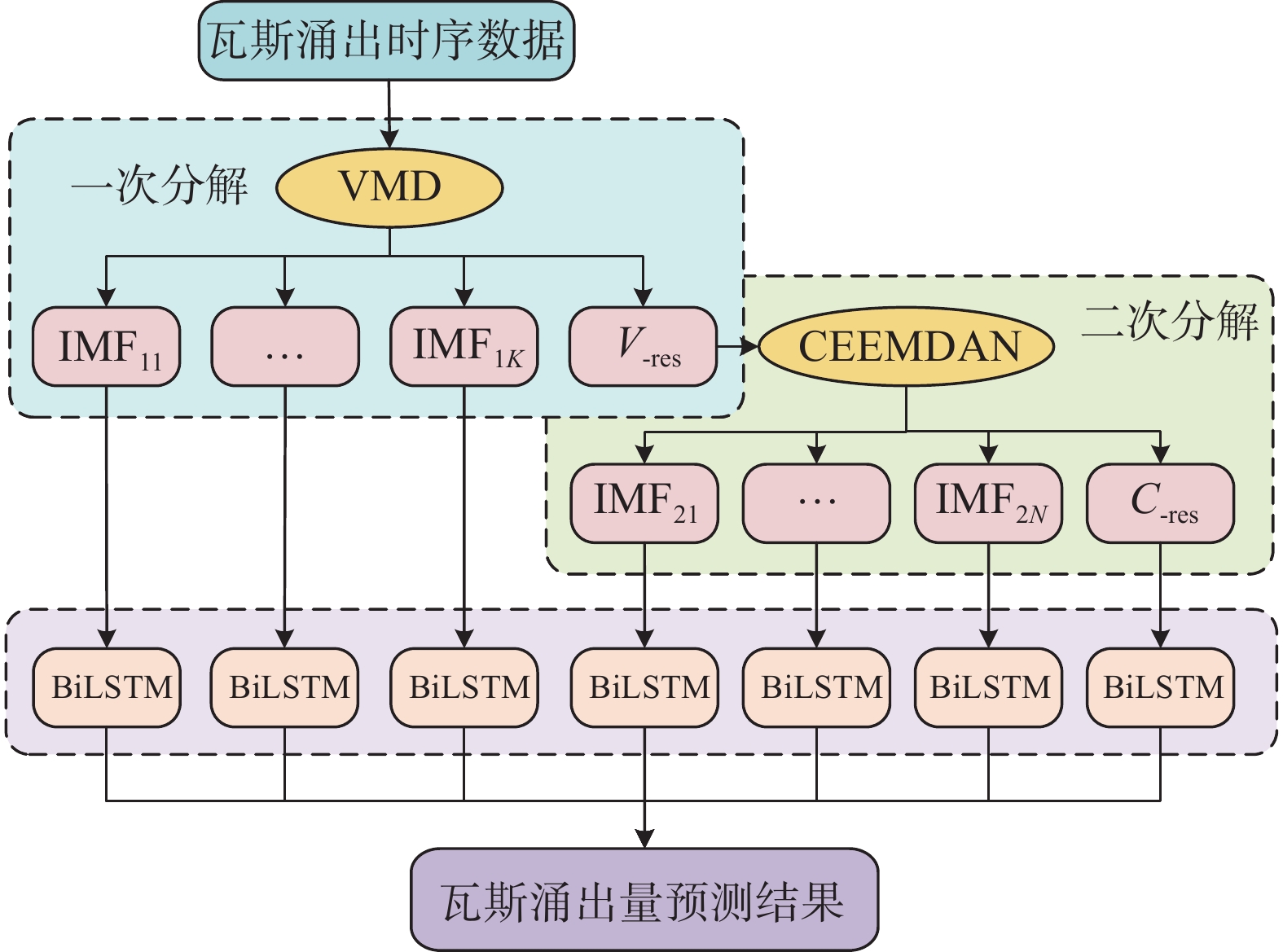
结合变分模态分解（VMD）、自适应噪声完备经验模态分解（CEEMDAN）、贝叶斯优化算法（BO）和双向长短期记忆神经网络（BiLSTM）这4种时间序列处理方法，建立了1种基于二次分解和BO-BiLSTM组合模型的采煤工作面瓦斯涌出量预测模型。VMD-CEEMDAN-BO-BiLSTM模型如图3所示。

图  3  VMD-CEEMDAN-BO-BiLSTM模型结构

Figure  3.  Structure of VMD-CEEMDAN-BO-BiLSTM model

下载: 全尺寸图片 幻灯片

预测具体步骤如下：

1）根据中心频率法确定VMD分解子序列的数量$ k $，采用VMD将瓦斯涌出量时间序列分解为$ k $个子序列。

2）利用VMD处理瓦斯涌出量时间序列后的残余分量，对残余分量进行CEEMDAN二次分解。

3）对经VMD一次分解和CEEMDAN二次分解后得到的所有子序列分别建立BO-BiLSTM模型，并进行训练和预测。

4）将步骤3）得到的各子序列预测结果进行叠加，得到瓦斯涌出量最终预测结果。

为验证模型预测性能，分别建立以下5种对照模型进行讨论。

对照模型1（VMD-BO-BiLSTM）：将瓦斯涌出量时间序列利用VMD进行分解，得到的子序列分别建立BO-BiLSTM模型进行预测。

对照模型2（CEEMDAN-BO-BiLSTM）：将瓦斯涌出量时间序列进行CEEMDAN分解，得到的子序列分别建立BO-BiLSTM模型进行预测。

对照模型3（BO-BiLSTM）：对瓦斯涌出量时间序列直接建立BO-BiLSTM模型进行预测。

对照模型4（BO-LSTM）：对瓦斯涌出量时间序列建立BO-LSTM模型进行预测。

对照模型5（BPNN）：对瓦斯涌出量时间序列建立BPNN模型进行预测。

2.2   瓦斯涌出量预测数据及数据处理

为验证模型预测效果，选取数据的时间段尽量有较高的相似性，最终采用陕西彬长某矿2种情景作为实验数据。①情景1，选取40205采煤工作面2020年3月2日至9月27日共210 d的绝对瓦斯涌出量日监测数据；②情景2，选取位于瓦斯富集区的40309采煤工作面2021年3月17日至10月11日共210 d的绝对瓦斯涌出量日监测数据。将2种情景数据的前170 d瓦斯涌出量时间序列作为训练集，后40 d瓦斯涌出量时间序列作为测试集。实验环境为Windows11操作系统，处理器型号为Intel Core i7-10870H CPU @ 2.20 GHz，软件环境借助MATLAB R2021a平台。

为提高模型预测精度，采用变分模态分解（VMD）算法对瓦斯涌出量时间序列进行分解，其中惩罚因子$\alpha $、保真度系数$\tau $和收敛停止条件$\beta $使用默认值。为避免数据过分解或欠分解，采用中心频率法确定$k$值。分别设置$k$=3、4、5、6、7、8、9，得到不同$k$值下每一个模态分量的中心频率。不同$k$值下模态分量中心频率见表1。

表  1  不同$k$值下模态分量中心频率

Table  1.  Center frequency of modal components at different $k$ values

模态分量	中心频率
	k=3	k=4	k=5	k=6	k=7	k=8	k=9
$u$1	0.354 29	0.421 08	0.354 57	0.415 59	0.429 79	0.430 29	0.455 04
$u$2	0.094 61	0.257 63	0.201 49	0.292 51	0.334 22	0.335 53	0.394 42
$u$3	0.000 15	0.084 48	0.098 50	0.180 64	0.260 37	0.264 32	0.325 69
$u$4	—	0.000 14	0.028 44	0.089 49	0.169 96	0.180 73	0.261 47
$u$5	—	—	0.000 06	0.024 43	0.086 40	0.101 27	0.179 83
$u$6	—	—	—	0.000 05	0.023 65	0.047 99	0.100 65
$u$7	—	—	—	—	0.000 05	0.014 58	0.047 49
$u$8	—	—	—	—	—	0.000 03	0.014 15
$u$9	—	—	—	—	—	—	0.000 03

下载: 导出CSV 

| 显示表格

根据表1中的数据：当$k$≤7时，分量间的中心频率差值相对较大，且随着$k$值的增加而逐渐减小；当$k$=8时，模态分量$u$₆、$u$₇的中心频率分别为0.04799、0.01458，与其他几个模态分量之间的倍数关系相比，$u$₆和$u$₇的中心频率相对较小，可认为$k$=8时数据被过度分解。因此，确定$k$=7为最佳分解模态数，由此得到分解后各模态分量，其中低频部分的IMF1和IMF2是瓦斯涌出时间序列的趋势项，显示了瓦斯涌出量时间序列的长期走势特点；RES为经VMD一次分解后得到的残余序列，利用CEEMDAN可将残余序列二次分解为6个子序列。

为提升预测性能，避免人为经验调参的不足，利用贝叶斯优化算法分别对各子序列BiLSTM预测模型（BO-BiLSTM）的神经元隐藏层数、隐藏层神经元个数、初始学习率和L2正则化各超参数进行优化及确定，并将时间滑动窗口设置为10，批处理大小设置为16。各子序列超参数搜索范围设置及贝叶斯优化结果为：①子序列IMF1，1层神经元隐藏层，神经元数73，学习率0.010 2，L2正则化为7.36×10⁻¹⁰；②子序列IMF2，1层神经元隐藏层，神经元数62，学习率0.010 0，L2正则化为5.75×10⁻⁹；③子序列IMF3，1层神经元隐藏层，神经元数84，学习率0.010 0，L2正则化为8.12×10⁻⁷；④子序列IMF4，1层神经元隐藏层，神经元数53，学习率0.010 0，L2正则化为2.33×10⁻⁶；⑤子序列IMF5，1层神经元隐藏层，神经元数56，学习率0.010 1，L2正则化为5.17×10⁻⁵；⑥子序列IMF6，1层神经元隐藏层，神经元数121，学习率0.011 1，L2正则化为9.58×10⁻³；⑦子序列IMF7，2层神经元隐藏层，神经元数177，学习率0.010 1，L2正则化为2.15×10⁻⁹。

3.   瓦斯涌出量预测结果

3.1   单步预测结果

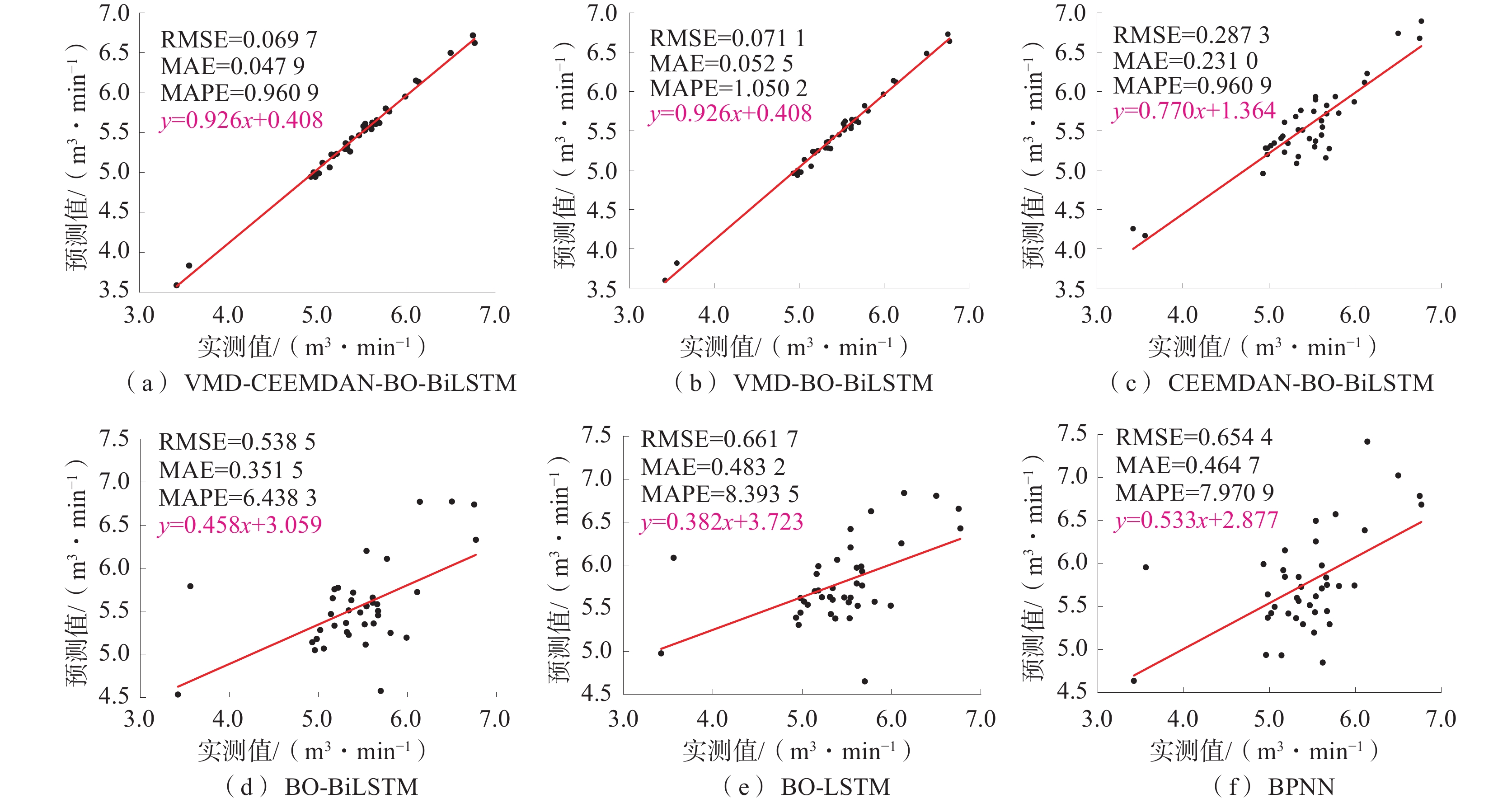
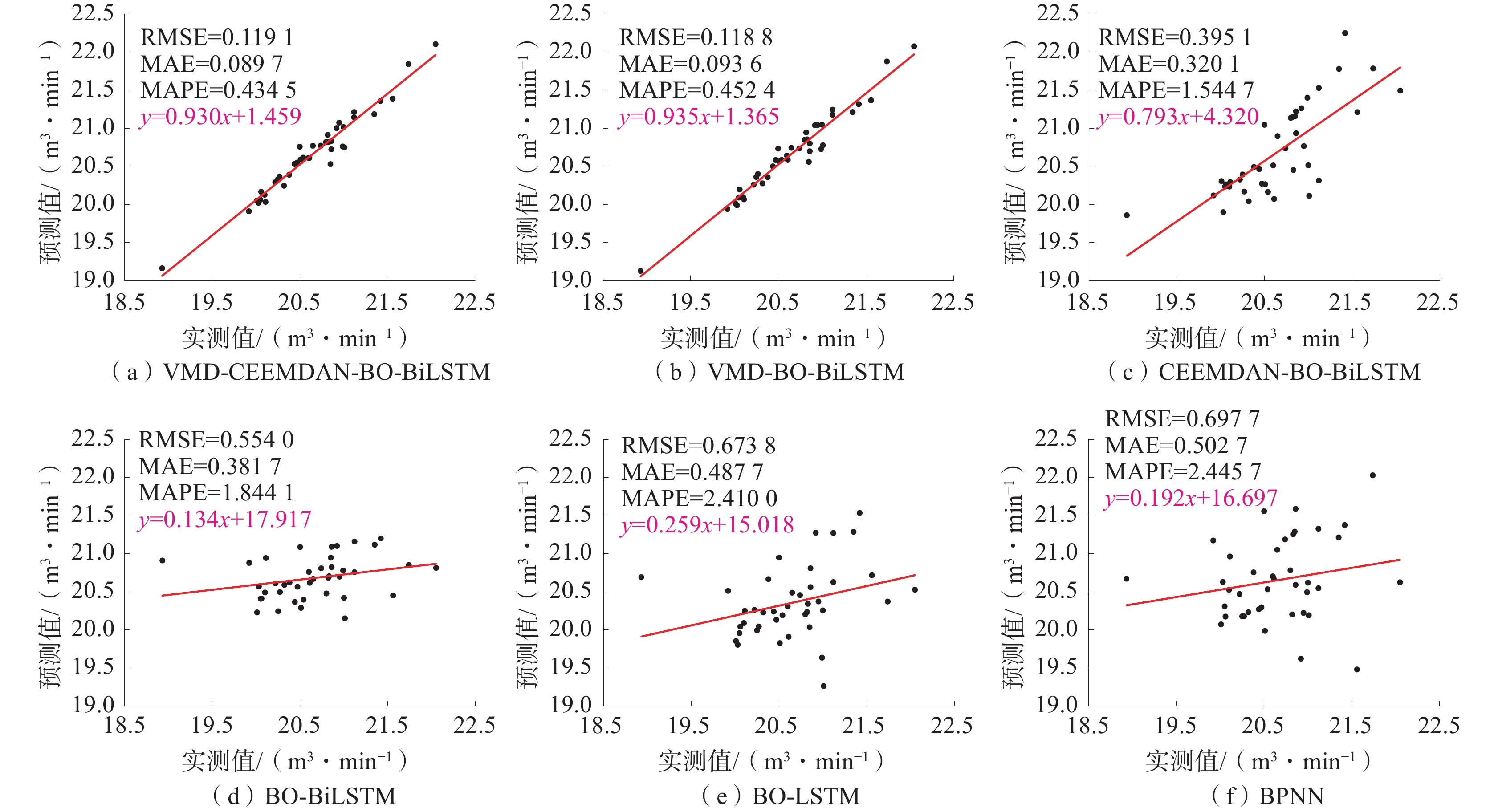
情景1各模型单步预测结果如图4所示，情景2各模型单步预测结果如图5所示。

图  4  情景1各模型单步预测结果

Figure  4.  Prediction results of each model in a single step of scenario 1

下载: 全尺寸图片 幻灯片

图  5  情景2各模型单步预测结果

Figure  5.  Prediction results of each model in a single step in scenario 2

下载: 全尺寸图片 幻灯片

总体来看，经过VMD和CEEMDAN算法分解后的预测模型均能较好地捕捉历史瓦斯涌出量时间序列的统计规律，实现较为理想的预测，说明借助信号分解算法的组合模型对瓦斯涌出量进行预测是切实可行的。对比不同模型预测结果可发现，与信号分解算法相结合后，各组合模型预测结果的预测值与实测值散点图相比单一BO-BiLSTM、BO-LSTM和BPNN的预测结果相关性更高，其预测偏差明显降低。即瓦斯涌出量时间序列经信号分解后的子序列更为规律，有助于机器学习算法捕获其非线性特征。

通过比较各模型误差指标发现：情景1中本文所提组合模型单步预测的RMSE、MAE、MAPE分别为0.069 7 m³/min、0.047 9 m³/min、0.9609%，除线性拟合公式与VMD-BO-BiLSTM模型的相同外，其余指标均优于对照模型；情景2中本文所提组合模型单步预测的RMSE、MAE、MAPE分别为0.119 1 m³/min、0.089 7 m³/min、0.4345%，除RMSE比VMD-BO-BiLSTM模型的略高外，其余指标均优于对照模型。由此说明本文所提VMD-CEEMDAN-BO-BiLSTM组合模型单步预测精度较高、优势较为明显。

3.2   多步预测结果

情景1各模型多步预测结果图如图6所示，情景2各模型多步预测结果如图7所示，各模型多步预测精度对比见表2。

图  6  情景1各模型多步预测结果

Figure  6.  Multi-step prediction results for each model of scenario 1

下载: 全尺寸图片 幻灯片

图  7  情景2各模型多步预测结果

Figure  7.  Multi-step prediction results for each model of scenario 2

下载: 全尺寸图片 幻灯片

表  2  各模型多步预测精度对比

Table  2.  Comparison of multi-step prediction accuracy of each model

预测方法	情景1									情景2
	RMSE			MAE			MAPE			RMSE			MAE			MAPE
	两步	三步		两步	三步		两步	三步		两步	三步		两步	三步		两步	三步
VMD-CEEMDAN- BO-BiLSTM	0.156	0.257		0.104	0.200		2.048	3.801		0.212	0.450		0.169	0.323		0.843	1.576
VMD-BO-BiLSTM	0.157	0.259		0.106	0.201		2.079	3.834		0.212	0.448		0.174	0.325		0.843	1.583
CEEMDAN-BO-BiLSTM	0.410	0.465		0.295	0.359		5.531	6.567		0.501	0.657		0.401	0.482		1.935	2.326
BO-BiLSTM	0.525	0.646		0.343	0.437		6.324	7.854		0.607	0.638		0.465	0.504		2.282	2.473
BO-LSTM	0.715	0.755		0.548	0.568		9.411	9.611		0.774	0.778		0.573	0.570		2.756	2.850
BPNN	0.796	0.875		0.609	0.675		10.44	10.94		0.744	1.018		0.600	0.773		2.993	3.615

下载: 导出CSV 

| 显示表格

由图6和图7可以看出：单一的BO-BiLSTM、BO-LSTM和BPNN模型预测效果较差，且预测结果出现了不同程度的错峰、错谷问题，难以应用于实际生产调度；当BO-BiLSTM模型与信号分解算法组合后，机器学习的预测精度显著提升，能够较为理想的预测坡、峰、谷等特征序列，其中CEEMDAN-BO-BiLSTM在局部范围内只能预测瓦斯涌出量序列的大体走势，与实际序列的吻合度较差，而VMD-CEEMDAN-BO-BiLSTM和VMD-BO-BiLSTM的预测效果较优，有效缓解了上述对照模型存在的问题；随着预测步长增大到3步，各模型预测序列与实际序列的吻合度均有一定程度的降低，符合统计学规律。

由表2可以看出：前2组模型的预测精度明显优于其余4组对照模型；本文模型的各项指标均稍优于VMD-BO-BiLSTM模型，且随着预测步长的增加，模型各项指标也随之有着不同程度的增大，综合单步预测结果分析，能够说明该模型在预测步长较短时，预测精度比较理想。

4.   结　语

根据采煤工作面瓦斯涌出量时间序列特征，构建了基于二次分解和BO-BiLSTM的瓦斯涌出量组合预测模型。将瓦斯涌出量时间序列经过VMD一次分解，利用其分解后的残余分量进行CEEMDAN二次分解，充分挖掘出瓦斯涌出量时序数据的非线性时间特征信息，能提高模型的整体预测精度。对分解所得各子序列分别建立BiLSTM预测模型，并引入贝叶斯算法优化各模型超参数，提升模型预测性能，避免了人为经验调参的不足。通过将VMD、CEEMDAN和BO-BiLSTM相结合建立组合预测模型，充分发挥了各算法在处理时间序列时各自的优势：一方面，VMD-CEEMDAN-BO-BiLSTM组合模型在单步预测中，与对照模型相比可靠性较高，预测值与实测值保持着相当高的吻合度；另一方面，VMD-CEEMDAN-BO-BiLSTM组合模型在多步预测中表现也不俗，预测精度能够满足实际需要。